Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Géometrie plane et dans l'espaceTopics traitant de Géometrie plane et dans l'espace [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Ensembles de Points Equidistants de droites

Posté par Enigma (invité) 07-05-05 à 01:10

slt a tous, je suis nouvelle ici et je decouvre votre site qu'il a l'air super d'autant que vous etes dotés du LaTex que je maitrise parfaitement ; alors voila mon probleme que je vous met en entier car je pense que c plus judicieux.

_________________________________________________________________________

On se propose d'etudier l'ensemble, noté 3$\sum des points de l'espace equidistants de deux droites 3$D et 3$D^' non coplanaire et orthogonales. L'espace est muni d'un repere orthonormal 3$(O;\vec{i};\vec{j};\vec{k}).
La droite 3$D passe par le point 3$A de coordonées 3$(0;0;1) et admet comme vecteur directeur 3$\vec{u} tel que 3$\vec{u}=\vec{i}+\vec{j}.
La droite 3$D^' passe par le point 3$B de coordonées 3$(0;0;-1) et admet comme vecteur directeur 3$\vec{v} tel que 3$\vec{v}=\vec{i}-\vec{j}


3$\rm\blue 1)
3$\rm\red a]
Verifier que 3$D et 3$D^' sont non coplanaire et orthogonales.

3$\rm\red b]
Montrer que le point 3$O appartient à 3$\sum


3$\rm\blue 2)
3$\rm\red a]
Montrer qu'une representation parametrique de 3$D est :
4$\rm\{{x=t\\y=t\\z=1}, t\in\mathbb{R}

3$\rm\red b]
3$M est un point de l'espace de coordonées 3$(x;y;z), determiner les coordonées du projeté orthogonal de 3$M sur la droite 3$D, en deduire la distance de 3$M à la droite 3$D.


3$\rm\blue 3)
Calculer de meme la distance de 3$M a la droite 3$D^'


3$\rm\blue 4)
En deduire que 3$M appartient à 3$\sum si et seuleument si on a : 3$xy+2z=0


3$\rm\blue 5)
Deduire de cette relation :

3$\rm\red a]
Que les intersections de 3$\sum avec des plans orthogonaux à la droite 3$(AB) sont en general des hyperboles. Preciser le cas d'exception ;

3$\rm\red b]
La nature des intersections de 3$\sum avec des plans orthogonaux a l'axe 3$(O;\vec{i}) ou a l'axe 3$(O;\vec{j})

_________________________________________________________________________

voila j'ai fait le plus claire que j'ai pu ; je prend des cours par correspondances et il est pour moi tres difficile de faire de tels exercices ; je bloque des la premiere question ... c un camarade qui m'a conseiller ce site et j'espere que vous pourrez faire quelque chose pour moi et en tout cas merci quand meme.

Posté par Enigma (invité)re : Ensembles de Points Equidistants de droites 07-05-05 à 16:19

slt a tous,

personne ne peut vraiment m'aider ?

Posté par rolands (invité)re : Ensembles de Points Equidistants de droites 07-05-05 à 19:20

Bonjour Enigma ,
1)a._Les droites D et D' sont // xOy et ont des vecteurs drirecteurs
non // ,elles ne sont pas dans un même plan .
_____Produit scalaire u.v=0 >>>   D et D'sont orthogonales .
1)b_OA est perpendiculaire à D et vaut 1,c'est la distance de O à D. ____De même OB =1 est la distance de B à D':donc O est dans Sigma.
2)a._D // xOy donc z=1 , D se projette sur xOy selon la bissectrice de xÔy , donc x=y  >>> d'où l'équation paramétrique de D .
2)b._essaie de poursuivre ,et exprime les difficultés que tu peux rencontrer ...
Bon courage .

Posté par Enigma (invité)re : Ensembles de Points Equidistants de droites 07-05-05 à 20:03

bonjour a tous ,

salut rolands voila ce que je comprend de ce que vous m'avez mis :

3$\textrm \blue 1)
3$\textrm \red a]

Le vecteur directeur de la droite 3$D etant 3$\vec{u}=\vec{i}+\vec{j} et le vecteur de la droite 3$D^' etant 3$\vec{v}=\vec{i}-\vec{j}, nous avons :

3$\vec{u}.\vec{v}=(\vec{i}+\vec{j}).(\vec{i}-\vec{j})=\vec{i}^2-\vec{j}^2

or 3$\vec{u}=\vec{j} ceux-ci etant des vecteurs unitaires soit :
3$\vec{u}^2=\vec{j}^2 donc 3$\vec{u}^2-\vec{j}^2=0 d'ou 3$\vec{u}.\vec{v}=0

d'ou le fait que 3$D et 3$D^' soient orthogonales.  

Ensuite je ne comprends ceci : Les droites D et D' sont // xOy et ont des vecteurs drirecteurs non // ,elles ne sont pas dans un même plan


3$\textrm \red b]
3$\vec{OA}\begin{pmatrix}x_A-x_O\\y_A-y_O\\z_A-z_O\end{pmatrix}  soit 3$\vec{OA}\begin{pmatrix}0-0\\0-0\\1-0\end{pmatrix} c'est a dire 3$\vec{OA}\begin{pmatrix}0\\0\\1\end{pmatrix} et donc 3$OA=\sqrt{0^2+0^2+1^2}=\sqrt{1^2}=1

de même :
3$\vec{OB}\begin{pmatrix}x_B-x_O\\y_B-y_O\\z_B-z_O\end{pmatrix}  soit 3$\vec{OB}\begin{pmatrix}0-0\\0-0\\-1-0\end{pmatrix} c'est a dire 3$\vec{OB}\begin{pmatrix}0\\0\\-1\end{pmatrix} et donc 3$OB=\sqrt{0^2+0^2+(-1)^2}=\sqrt{(-1)^2}=1

donc 3$O est equidistant de 3$A et 3$B  ; or 3$A appartient a 3$D et 3$B appartient a 3$D^' donc 3$O est equidistant de 3$D et 3$D^' et appartient donc à 3$\sum par definition de cette ensemble.


3$\textrm \blue 2)
3$\textrm \red a]
Ensuite je ne comprends ceci :D // xOy donc z=1 , D se projette sur xOy selon la bissectrice de x0y , donc x=y  >>> d'où l'équation paramétrique de D.

___________________________________________________________________

visiblement j'ai du mal a comprendre ceci xOy

merci pour le temps que vous consacrer pour moi.





Posté par Enigma (invité)re : Ensembles de Points Equidistants de droites 07-05-05 à 21:55

rebonsoir a tous ,

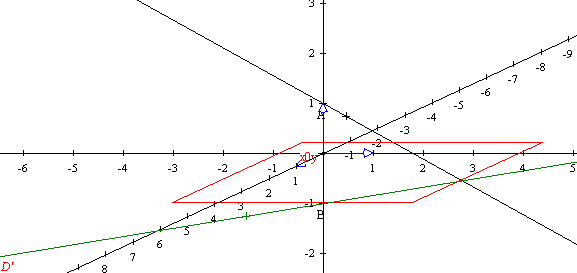
j'ai pu a l'aide d'un logiciel tenté une representation de la situation en esperant que cela puisse m'aider mais en vain ; je vous joint le document

merci pour l'aide.

Ensembles de Points Equidistants de droites

Posté par rolands (invité)re : Ensembles de Points Equidistants de droites 07-05-05 à 23:11

Ce n'est pas tout à fait cela : U n'est pas un vecteur unitaire,les vecteurs unitaires sont i ,j et k .
u.v =i²-j²=(1)-(1)=0 (car i et j sont unitaires).
Pour la question 1)b) Tu te compliques la tâche:OA a pour longueur 1
par définition du point A . De même OB=1 .
2)a_ D a pour vecteur directeur u=i+j ,on voit que la composante de u sur l'axe Oz est nulle ;donc u (et donc D) est // au plan (Ox,Oy) qu'on désigne xOy .
i+j est la bissectrice de l'angle xOy : un point de cette bissectrice est à égale distance de Ox et de Oy ,c'est à dire que ce point aura une abscisse = à son ordonnée ,c'est ce que je note x=y ;c'est aussi le cas pour un point de D.
Tous les points de D ont z=1 et x=y :d'où l'équation paramétrique de D : x=t , y=t ,z=1.
J'espère que tu as compris,pose des questions,tu auras l'aide que tu souhaites.
Je continue tout à l'heure .    

Posté par rolands (invité)re : Ensembles de Points Equidistants de droites 08-05-05 à 00:02

2)b._ M (x,y,z) soit X un point de D : X (t,t,1).
_____MX a pour composantes (t-x;t-y;1-z).
_____MX²=(t-x)²+(t-y)²+(1-z)²=2t²-2t(x+y)+x²+y²+z²-2z+1 .
_____MX² sera minimum quand sa dérivée (MX²)' sera nulle,et alors X   ______sera la projection H de M sur D.
__ (MX²)'=4t-2(x+y) sera nul pour t=(x+y)/2.
__ H a donc pour coordonnées ((x+y)/2;(x+y)/2;1)
d'où MH² , d'où MH .
3) Même chose pour avoir la distance de M à D'.
4) En écrivant que les distances de M à D et D' sont égales ...
...........dis moi où tu en es ...    

Posté par Enigma (invité)re : Ensembles de Points Equidistants de droites 08-05-05 à 00:06

rebonsoir a tous,

salut rolands et encore merci pour l'aide que vous m'apporter.

_______________________________________________________________________

en fait je me suis tromper :

3$\rm \blue 1)
3$\rm \red a]
3$\vec{i}=\vec{j} ceux ci etant des vecteurs unitaires soit

3$\vec{i}^2=\vec{j}^2 donc 3$\vec{i}^2-\vec{j}^2=0 d'ou 3$\vec{u}.\vec{v}=0

d'ou le fait que 3$D et 3$D^' soient orthogonales.

Ensuite je ne comprends ceci : Les droites D et D' sont // xOy et ont des vecteurs drirecteurs non // ,elles ne sont pas dans un même plan

j'essaye en ce moment de comprendre la suite.

Posté par Enigma (invité)re : Ensembles de Points Equidistants de droites 08-05-05 à 00:12

voila ma question precise concernant cette question :

pourquoi le fait qu'un vecteur directeur de 3$D soit 3$\vec{u}=\vec{i}+\vec{j} et qu'un directeur de 3$D^' soit 3$\vec{v}=\vec{i}-\vec{j} montre que 3$D et 3$D^' sont non coplanaires ?

Posté par
Nightmarere : Ensembles de Points Equidistants de droites 08-05-05 à 00:35

Bonjour

Démontrer que le produit vectoriel 3$\rm\vec{u}\wedge\vec{v}=\vec{0} ce qui prouvera que tes deux vecteurs donc que les droites ne sont pas coplanaires


Jord

Posté par rolands (invité)re : Ensembles de Points Equidistants de droites 08-05-05 à 06:11

Bonjour Nightmare ,
Que le produit vectoriel de 2 vecteurs (en l'occurence u et v portés par D et D')soit nul ne suffit pas à démontrer que ces 2 droites ne sont pas coplanaires : il faut de plus que ces 2 vecteurs ne soient pas // (ce qui est le cas) et qu'un point de D' (B) ne soit pas dans le plan (A,u,v).

Posté par rolands (invité)re : Ensembles de Points Equidistants de droites 08-05-05 à 06:53

Bonjour Enigma ,
Je réponds à ta question :
u.v=0 montre que u et v sont orthogonaux (ce qu'on te demandaient de montrer) et qu'ils définissent une direction de plan : en l'occurence un plan //à xOy.Pour que D et D' ne soient pas coplanaires , il faut préciser que B (porté par D') n'est pas dans le plan //à xOy passant par A .

Posté par rolands (invité)re : Ensembles de Points Equidistants de droites 08-05-05 à 11:00

Bonjour Enigma ,
je vais terminer car je m'absente pour 8 jours .
3)ATTENTION , une équation paramétrique de D' est (x=t;y=-t;z=-1).
J'espère que tu as trouvé que MH²=(y-x)²/2 +(1-z)²,et si K est la projection de M sur D'        MK²=(x+y)²/2 +(1+z)².
4)En égalant MH²=MK² ...beaucoup de choses s'éliminent et tu trouves :
_____xy+2z=0 ____
5)a)__un plan orthogonal à AB a pour équation z=constante.
      1) si cette constante est non nulle, xy+2z=0 devient xy=Cte , ce qui représente une hyperbole équilatère .
      2) si Cte=0 alors xy=0 qui a pour solutions x=0 et y=0.
         x=0 et z=0   c'est la droite y'Oy
         y=0 et z=0   c'est la droitr x'Ox :l'hyperbole  
         est ramenée à ses axes ,on dit qu'elle est dégénérée.
5)b) raisonne de la même manière , et j'espère que tu y arrives.
...je te souhaite bon courage , accrche-toi .

Posté par Ange38 (invité)re : Ensembles de Points Equidistants de droites 31-01-07 à 15:55

Bonjour à tous !

Je fais remonter à la surface un très vieux post, mais j'ai le même exercice à faire en DM de maths spé. Il y a une question que je n'arrive toujours pas à finir, étant donné en plus qu'il y a une partie de la question que je n'ai pas à faire.

C'est presque la même question que la 2b de l'énoncé plus haut, voici les deux points qui me bloquent :

1- Soit M(x;y;z). Calculer la distance de M à la droite D. (ici, pas de projeté orthigonal)
2- Calculer de même la distance de M à la droite D'.

Je n'arrive pas à obtenir les mêmes distances que celles plus haut, et du coup je ne peux pas avancer sur une autre question qui est la 4 de l'énoncé en début de post.

Merci d'avance à ceux qui pourront me débloquer
A bientôt !


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !