Bonsoir,
Tu commences mal :relis toi!

A oui merci je crois comprendre ... c'est le carré que j'ai mal appliqué  je vais refaire ca, en ce qui concerne la valeur absolue, il faudrait que je considère l'autre  option du coup ?

Sois rigoureux...valeur absolue?
A quelle condition la racine carrée existe? etc....

Effectivement ca n'aurai pas de sens ..

J'ai donc refait, j'ai retrouvé quelques chose de plus cohérent de la forme :
         4x²+4ax+a²-x=0
<=>4x²+x(-1+4a)+a²=0

En développant mon Δ je trouve 1-16a, je fais l'étude du signe et je conlcu sur le nombre de solution par rapport aux valeurs prises par a.

Je pense que cette fois ci c'est bon, Merci beaucoup

Eventuellement , tu peux t'aider d'une représentation graphique en faisant varier a pour te guider un peu ...

Attention : dejà ton discriminant est faux.

oui .. Δ=1-8a plutot il me semble mais même conlcusion du coup.. Remerci

Et tu n'as rien d'autre à dire ?

Utilise ce que je t'ai écrit à 22h07 et regarde si tu n'as pas de contradictions avec tes conclusions.

Hm je ne trouve pas ?
  je conlcu simplement en disant :
    Si 1-8a=0 <=> a=1/8 alors l'équation de l'exo n'a qu'une solution dans IR
    et Si 1-8a>0 <=> a<1/8 alors l'equation a donc 2 solutions dans IR
    et donc logiquement si  a > 1/8 alors l'equation n'a pas de solutions dans IR (mais deux complexes conjuguées dans C, il faut que je l'évoque ?)
On ne me demande pas de les calculer donc je conclu simplement avec ce qui est dit précedemment, j'ai manqué quelque chose ?

Que penses tu du deuxieme cas?

J'insiste sur la représentation graphique qui t'aide pour ton erreur.

Je dois partir là : à demain si personne n'a pris le relai .

Je crois que je vois l'idée si a est trop petit alors 2x+a sera négatif ce qui est impossible. Pour ce qui est de la représentation graphique j'avoue que j'essaie  mais je ne comprends pas plus

Merci quand même l'aide et la réactivité

J'ai réussi à faire la représentation graphique et rien ne me choque pour le coup les solutions que l'on cherche sont celles pour lesquelles y=0 et peu importe ou jusqu'où je fais varier a dans les négatifs il y a bien deux solutions, j'avoue que la je ne comprends pas ma faute

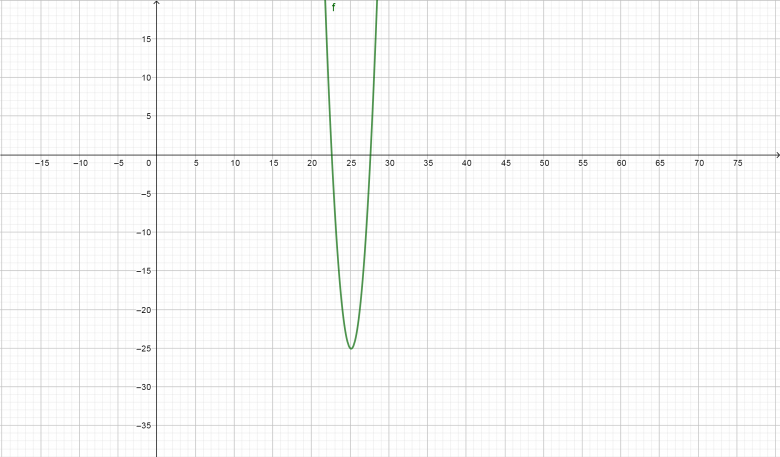
Bonjour,
Comme on ne sait pas ce que tu as représenté, on ne peut pas interpréter ton graphique.

Je pense que philgr22 envisageait la courbe de la fonction racine carrée
et de faire varier la droite d'équation y = 2x+a .
La droite varie parallèlement à elle même, et on peut voir que très souvent il n'y a qu'une solution.

Plus convainquant sans doute :
Que trouves-tu pour le cas numérique a = -15 ?

Merci pour votre réponse, je regarde ca cette après midi. Je visualise bien le problème en imaginant la représentation graphique cette fois

Alors en imaginant la représentation graphique je pense avoir compris ce qui n'allait pas.
Effectivement  on trouvais bien l'équation : 4x²+x(4a-1)+a²=0 en développant le √x=2x+a du début de l'exercice
De la on trouvais bien Δ=-8a+a et en étudiant le signe on trouvais bien Δ=0 si a=1/8 ce qui se vérifie vite graphiquement
  Ce qui nous laisse donc avec le cas ou Δ>0 <=> -8a+1>0
                                                                                                <=> a<1/8
De la découle  les 2 racines dont une est vérifiée pour ∀a<1/8. Pour l'autre on a :
  x₂=

Mince je finis ici :
  x₁=[-4a+1-√(-8a+1)]/8
Or x existe SSI x>0 car il doit être solution de l'eq √x=2x+a et le x sous la racine ne peut être négatif..
  Ainsi x existe SSI : (-4a+1)/8 > [√(8a+a)]/8
                                 <=> a<0   (je raccourcis, c'est long à taper)
Or on sait que x₁ n'existe que si a<1/8
Comme il ne peut pas être négatif, finalement x₁ n'existe que si 0<=a<8

On conclu donc, √x=2x+a à une sol lorsque a est la racine double mais aussi quand a<0, si 0<=a<1/8, alors il y a deux sol et si a>1/8 alors il n'y a pas de solutions !

Cette fois ci je ne pense pas mettre trompé c'est en adéquation avec la représentation graphique

Ta conclusion est bonne.
Deux remarques :
Avec ta méthode, non seulement il faut x 0 , mais aussi 2x+a 0 .
En effet A = B n'est pas équivalent à A² = B².
Tu risques de tomber sur des solutions de x = -(2x+a)

Une autre méthode permet de moins 'embêter :
Poser X = x.
Chercher le nombre de solutions positives ou nulles de X = 2X²+a .

Merci beaucoup, effectivement cette méthode est beaucoup plus simple même si il y a beaucoup de similarité. On est d'accord que je n'ai pas besoin de revenir a la forme  √x = X à la fin puisque l'on cherche le nombre de solutions de  √x=2x+a en fonction des valeurs de a ?

On est d'accord si tu as cherché les solutions positives ou nulles pour X.

Oui, en tout cas merci !

De rien, et à une autre fois sur l'île