Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Nombres complexesTopics traitant de nombres complexes [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Equation de cercle avec des modules de complexes

Posté par
Estxlle 23-12-10 à 19:54

Bonjour tout le monde.

Alors voilà, je recherche de l'aide pour un Devoir maison de mathématiques niveau Terminale S.
Ce devoir maison traite les Nombres complexes mais particulièrement, les nombres complexes et leurs modules.
Voici l'énoncé de mon exercice, au fur et à mesure je vais vous expliquer ce que j'arrive à faire ou non.

Exercice n°2:
On se place dans le plan complexe muni d'un repère orthonormé direct (O;,)
On nomme A et B les points d'affixes respectives -2i et -4+2i
Soit f la fonction qui, à tout point M distinct de B, associe le point M' d'affixe z' = (iz-2)/(z+4-2i)

1) Soit M un point quelconque distinct de B et M' son image par f. Démontrer que OM'= (AM)/(BM)
---> J'ai réussi à démontrer cette question.

2) Démontrer et construire l'ensemble (E1) des points M(z) dont l'image M' est sur le cercle de centre O et de rayon 1.
---> J'ai trouvé que l'ensemble (E1) était sur la droite d'équation y = -8x-16 (J'espère ne pas avoir fais de faute de calcul)

3)Déterminer et construire l'ensemble (E2) des points M(z) dont l'image M' est sur le cercle de centre O et de rayon 2.
---> Et c'est ici que je coince.
Voilà mon calcul : Puisque que OM'= (AM)/(BM) alors on a :
(z-2i)/(z+4-2i)=2
(z-2i)= 2(z+4-2i) On pose z= x+iy et on obtient : (x+iy-2i) = 2x+2iy+8-4i
x+i(y-2) = (2x+8)+i(2y-4)
=
x²+y²-4y+4 = 4x²+32x+64+4y²-16y+16
-3x²-3y²+12y+32x-76
Cette équation de cercle est impossible, donc j'en ai conclue que ce n'était pas une équation de cercle mais je ne vois pas comment me dépatouiller de cette équation

4)Soit M un point quelconque distinct de B et M' son image par f:
*Démontrer que (mes parenthèses représentent les modules dans cette question )(z'-i)(z+4-2i) = 4
* Démontrer que si un point M(z)décrit le cercle (C1) de centre B et de rayon 2 alors M'(z') décrit un cerce dont on précisera le centre et le rayon.
---> Je n'ai pas encore réfléchi à cette question.

Merci d'avoir pris le temps de lire cet exercice et merci aussi de m'accorder un peu de temps.
Je vous souhaite de Joyeuses Fêtes à tous et beaucoup de bonnes choses.

Posté par
Trikzerre : Equation de cercle avec des modules de complexes 23-12-10 à 20:44

bonsoir. non pour la question 2 évite de passer directement à x+iy mais écris plutot module z'=2 après  tu passes en module dans ton expression de départ tu arranges un petit peu et tu obtiendras ton ensemble facilement..

Posté par
littleguyre : Equation de cercle avec des modules de complexes 23-12-10 à 20:50

Bonjour

Pour la 2) je n'ai pas vérifié ton calcul, mais tu aurais pu utiliser le résultat de la 1) :

M' appartient au cercle de centre O et de rayon 1 équivaut à OM' = 1, donc à AM/BM = 1, soit encore
MA = MB

Donc l'ensemble cherché est la médiatrice de [AB]

Pour la 3) tu confonds complexe et module de ce complexe : OM' = 2 n'équivaut pas à (z-2i)/(z+4-2i)=2, mais à
|(z-2i)/(z+4-2i)| = 2

Tu peux aussi regarder ici : [url]https://www.ilemaths.net/sujet-dans-un-plan-complexe-396287.html
[/url]

Posté par
littleguyre : Equation de cercle avec des modules de complexes 23-12-10 à 20:53

Le lien est celui-ci : Dans un plan complexe.

Posté par
Estxllere : Equation de cercle avec des modules de complexes 23-12-10 à 22:00

Cher Littleguy . J'ai remarqué que l'exercice posté Par Mélaniiie était exactement le même que le mien, en outre j'ai mené ma petite enquête et c'est bien Mélanie de ma classe.
Donc merci, pour ce précieux lien qui me sera très utile pour la question n°4.

Pour la question n°2, j'avais utilisé la même méthode que celle que tu as proposé sur l'exercice de Mélanie donc sauf erreur de calcul je pense que j'ai le bon raisonnement et le bon résultat.

Pour ce qu'il en est à présent, j'aimerais trouvé comment me dépatouiller de la question 3)
Je ne comprend pas la différence entre

Citation :
OM' = 2 n'équivaut pas à (z-2i)/(z+4-2i)=2, mais à
|(z-2i)/(z+4-2i)| = 2


Peux tu me donner quelques renseignements ou indices stp

Merci



Ai-je besoin de vous précisez que mon niveau en maths n'est guère élevé ?

Posté par
littleguyre : Equation de cercle avec des modules de complexes 23-12-10 à 22:04

(z-2i)/(z+4-2i) est un complexe

|(z-2i)/(z+4-2i)| est un réel positif.

C'est comme si tu écrivais que z = |z| ; ça ne colle pas ... (sauf si z est réel positif)

Posté par
Estxllere : Equation de cercle avec des modules de complexes 23-12-10 à 22:14

Du coup j'obtiens, |z-2i|/|z+4-2i| =2 ?

Mais il y a une règle de calcul spéciale à appliquer ?

Il n'y a pourtant pas de différence entre la question n°2 et la question n°3 Alors pourquoi n'arrive-je donc pas à y répondre ?

Posté par
Estxllere : Equation de cercle avec des modules de complexes 24-12-10 à 15:29

Cher littleGuy, c'est encore moi :/
Est ce que tu pourrais continuer de me donner un petit coup de pouce stp

Citation :
Du coup j'obtiens, |z-2i|/|z+4-2i| =2 ?

Mais il y a une règle de calcul spéciale à appliquer ?

Il n'y a pourtant pas de différence entre la question n°2 et la question n°3 Alors pourquoi n'arrive-je donc pas à y répondre ?


Merci d'avance.

Posté par
littleguyre : Equation de cercle avec des modules de complexes 24-12-10 à 15:35

La question 2 est une application simple et quasi immédiate de la question 1.

En revanche, appliquer le résultat de la question 1 à la question 3 s'avère plus laborieux (ou j'ai raté quelque chose) :

OM' = 2 équivaut à MA/MB = 2, soit encore à MA = 2MB
Ce qui se traduit par |x+i(y+2)| = 2|x+4+i(y-2)|
On obtient alors l'équation x²+(y+2)² = 4[(x+4)²+(y-2)²]

Après quelques calculs (x+\frac{16}{3})^2+(y-\frac{10}{3})^2=\frac{128}{9}

L'ensemble cherché est donc le cercle de centre I(-16/3 ;10/3) et de rayon \frac{8\sqrt{2}}{3}

On pourrait également procéder en utilisant des connaissances de premières (barycentre et produit scalaire) :

MA/MB = 2 équivaut successivement à

MA = 2MB
MA²=4MB²
MA²-4MB²=0
\vec{MA}^2-4\vec{MB}^2=0
(\vec{MA}+2\vec{MB}).(\vec{MA}-2\vec{MB})=0
(3\vec{MG_1}).(-\vec{MG_2})=0 avec G1 barycentre de (A,1),(B,2) et G2 barycentre de (A,1),(B,-2)

\vec{MG_1}.\vec{MG_2}=0

Donc l'ensemble cherché est le cercle de diamètre [G_1G_2].

Calculs à vérifier et éventuelles fautes de frappe à rectifier bien sûr.

Ceci me paraît compliqué par rapport aux autres questions. Sans doute y a-t-il beaucoup plus simple mais pour l'instant cela m'échappe

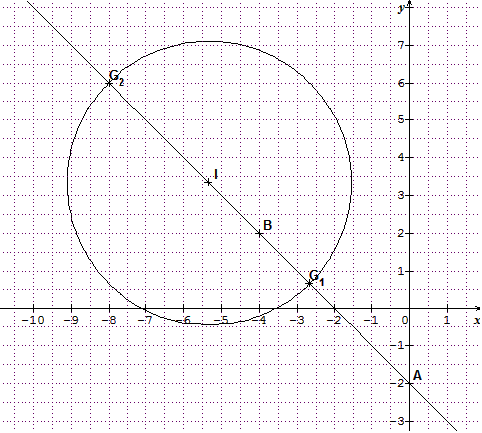
Equation de cercle avec des modules de complexes

Posté par
Estxllere : Equation de cercle avec des modules de complexes 24-12-10 à 15:40

Comment trouves-tu tes chiffres :

Citation :
On obtient alors l'équation x²+(y+2)² = 4[(x+4)²+(y-2)²]

Après quelques calculs (x+\frac{16}{3})^2+(y-\frac{10}{3})^2=\frac{128}{9}
?

Posté par
littleguyre : Equation de cercle avec des modules de complexes 24-12-10 à 17:35

|x+i(y+2)| = 2|x+4+i(y-2)|

En élevant au carré : |x+i(y+2)|² = 4|x+4+i(y-2)|²,

D'où : x²+(y+2)² = 4[(x+4)²+(y-2)²]

Après développement : -3x²-3y²-32x+20y-76 = 0

On divise par -3 ; on obtient x^2+y^2+\frac{32}{3}x-\frac{20}{3}y+\frac{76}{3}=0

Puis méthode classique (« forme canonique ») et on aboutit à :

(x+\frac{16}{3})^2+(y-\frac{10}{3})^2=\frac{128}{9} \\

Posté par
Estxllere : Equation de cercle avec des modules de complexes 25-12-10 à 17:31

Ah d'accords. Bon alors je vais refaire le calcul toute seule et me lancer dans la suite du Dm.
Merci beaucoup pour tes explications qui me sont très utiles, c'est très gentil de prendre du temps pour mes petits soucis

Joyeux Noël (a)
Estelle

Posté par
littleguyre : Equation de cercle avec des modules de complexes 25-12-10 à 19:33

Posté par
Estxllere : Equation de cercle avec des modules de complexes 30-12-10 à 16:40

Bonjour à tous, c'est à nouveau moi. Décidément cet exercice me pose pas mal de problèmes

Je reprend là où je me suis arrêtée, c'est à dire à la question n°4.
Revoici l'énoncé : Soit M un point quelconque distinct de B et M' son image par f.
   • Démontrer que │z'-i││z+4-2i│ = 42
   • Démontrer que si un point M(z) décrit le cercle (C1) de centre B et de rayon 2 alors M'(z') décrit un cercle dont on précisera le centre et le rayon.

Pour répondre à la première puce, voici le calcul que j'ai fais :
z'=│z+2i│/│z+4-2i│
z'-i = (│z+2i│/│z+4-2i│)-i
z'-i = (│z+2i│-i│z+4-2i│)/│z+4-2i│(**)
│z'-i││z+4-2i│=│z+2i│+i│z+4-2i│
│z'-i││z+4-2i│=│x+iy+2i│+ i│x+iy+4-2i│
│z'-i││z+4-2i│=│x+i(y+2)│+ i│x+4+i(y-2)│
│z'-i││z+4-2i│= x²+(y+2)²+ i²[(x+4)²+(y-2)²]
│z'-i││z+4-2i│= x²+ y²+ 4y+ 4-x²-8x-16-y²+4y-4
│z'-i││z+4-2i│=8y-8x-16

(**) Je ne suis pas sur de pouvoir passer de z'-i = │z'-i│

Donc voici mon calcul et mon raisonnement mais le problème c'est que je ne trouve pas du tout 42
Est-ce la bonne méthode ?

Posté par
littleguyre : Equation de cercle avec des modules de complexes 30-12-10 à 16:48

Citation :
Je ne suis pas sur de pouvoir passer de z'-i = │z'-i│
Tu as raison de douter. Tu n'as pas le droit (voir post du 23/12 à 22:04)

De plus ta 7ème ligne est fausse (dans le membre de droite tu sembles prendre le carré du module au lieu du module)

Posté par
littleguyre : Equation de cercle avec des modules de complexes 30-12-10 à 16:54

z'-i=\frac{iz-2}{z+4-2i}-i

Mets le membre de droite sous le même dénominateur

Puis produit en croix

Puis passages aux modules (sans remplacer z par x+iy)

Posté par
Estxllere : Equation de cercle avec des modules de complexes 30-12-10 à 17:03

Ok je tente cela. A tout de suite.

Posté par
Estxllere : Equation de cercle avec des modules de complexes 30-12-10 à 17:16

Alors voilà pour ce qu'il en est de mettre le membre de droite sous le même dénominateur et de faire le produit en croix :

Citation :
z'-i=\frac{iz-2}{z+4-2i}-i

z'-i = iz-2/z+4-2i - i(z+4-2i)/z+4-2i
z'-i = iz-2-iz-4i+2/z+4-2i
z'-i = -4i/z+4-2i
(z'-i)(z+4-2i) = -4i

Jusque là c'est bon ?

Posté par
littleguyre : Equation de cercle avec des modules de complexes 30-12-10 à 17:20

Il manque des parenthèses indispensables pour pouvoir te suivre. Le résultat final me semble faux.

Posté par
Estxllere : Equation de cercle avec des modules de complexes 30-12-10 à 17:31

Haaaaaan  :-x Ça commence à me prendre la tête

J'ai refais le calcul, avec des parenthèses mais je retrouve la même chose :

z'-i = [iz-2/z+4-2i] - [i(z+4-2i)/z+4-2i]
z'-i = [iz-2/z+4-2i]- [iz+4i-2/z+4-2i]
z'-i = [iz-2-iz-4i+2/z+4-2i]
z'-i = -4i/z+4-2i
(z'-i)(z+4-2i) = -4i

Posté par
littleguyre : Equation de cercle avec des modules de complexes 30-12-10 à 17:39

Il manque encore beaucoup de parenthèses.

\Large z^'-i=\frac{iz-2}{z+4-2i}-i=\frac{(iz-2)-i(z+4-2i)}{z+4-2i}

\Large z^'-i=\frac{iz-2-iz-4i-2)}{z+4-2i}=\frac{-4-4i}{z+4-2i}

Sauf erreur

Posté par
Estxllere : Equation de cercle avec des modules de complexes 30-12-10 à 18:01

Ah oui, j'avais pas le -4-4i car je pensais que i²=1 alors que i²=-1 c'est donc ici que vient mon erreur.
merci beaucoup

Posté par
littleguyre : Equation de cercle avec des modules de complexes 30-12-10 à 18:24

Il reste quand même quelque chose à faire pour conclure...

Posté par
Estxllere : Equation de cercle avec des modules de complexes 30-12-10 à 18:33

Oui, je dois faire le produit en croix et passer aux modules.

Posté par
Estxllere : Equation de cercle avec des modules de complexes 30-12-10 à 21:22

J'ai à présent fini mon Dm de mathématiques. Je vous remercie vraiment beaucoup pour votre patience et votre gentillesse.
Bonne année
Estelle

Posté par
littleguyre : Equation de cercle avec des modules de complexes 30-12-10 à 22:20


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1755 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !