Inscription / Connexion Nouveau Sujet
Équation de cercle et nombre complexe
Alors bonjour/bonsoir à tous, ceci est mon premier pas sur le forum !
Je bloque sur un exercice que voici:
Le plan complexe est rapporté au repère orthonormé direct (O;OU;OV).
On note f la fonction qui, à tout point M d'affixe z =/= -1 , associe le point M' d'affixe z' telle que:
z' = f(z) = (-iz-2)/(z+1)
On se propose de rechercher en utilisant deux méthodes, l'ensemble (E) des points M tels que M' appartient à l'axe des abscisses, privé de 0.
1) Méthode analytique.
x et y désignent deux nombres réels tous les deux non nuls.
a) Développer l'expression (x+(1/2))²+(y-1)²
Je trouve x²+y²x-2y+(5/4)
b) On pose z=x+iy , exprimer Im(z') en fonction de x et y.
Je trouve Im(z')= (y²-2y-x²-x)/((x+1)²+y²)
c) En déduire l'ensemble (E) des points M lorsque M' appartient à l'axe des abscisses, privé de 0.
C'est à ce moment que j'vois pas quel lien on doit faire!
Ce que je sais: M' appartient à l'axe des abscisses si Im(z')=0
2) Méthode géométrique.
a) Démontrer que, pour tout nombre complexe z =/= -1 , z' = -iW où W=(z-2i)/(z+1)
-iW= i*[(z-2i)/(z+1)] ce qui revient bien à z' soit (-iz-2)/(z+1)
b) A et B sont les points d'affixes respectives 2i et -1. Donner une interprétation géométrique d'un argument de W lorsque z =/= 2i.
Pour cette question je vois pas trop ce qu'est une interprétation géométrique mais en restant sur ce que je sais du cours j'arrive à:
arg(W) = arg( (z-2i)/(z+1) ) = arg( (z-zA)/(z-zB) ) et là j'vois plus trop la suite...
c) Exprimer arg(z') en fonction de arg(W).
d) Déduire de ce qui précède l'ensemble (E).
Bonjour Park et bienvenue sur l'
a) Dans ton développement , il manque un signe ( erreur de frappe probablement )
x² + y²+ x - 2y + (5/4)
b) pour Im(z'), je trouve -(x²+x+y²-2y)/((x+1)²+y²) , et là , le lien devient plus apparent
c) Il faut effectivement que Im(z') soit égal à 0
Donc x²+x+y²-2y = 0
Or x² +x + y² - 2y + (5/4) = (x+(1/2))²+(y-1)² donc ...
Je te laisse continuer
Pour la méthode géométrique:
arg(W) = arg( (z-2i)/(z+1) ) = arg( (z-zA)/(z-zB) ) =
Ensuite arg(z') = arg(-iW) = ....
Comme arg(z')doit être égal à k , on peut en tirer des conclusions sur
, on peut en tirer des conclusions sur , et puis sur la position de M par rapport à A et à B
Pour la question C) du 1)
Si je continue:
(5/4) = (x+(1/2))²+(y-1)² et j'doute aller plus loin car je ne vois pas à quoi sert ce "(x+(1/2))²+(y-1)²"
Je vois juste que l'ensemble des points M' ce situe sur l'axe des abscisses (sauf 0) mais pour voir l'ensemble M quel est le lien ? ( Vu le contexte j'dirais que (E) est un cercle ou une partie d'un cercle mais je ne vois rien qui associe quelque chose à un cercle )
Et pour la c) du 2) On doit exprimer arg(z') en fonction de arg(w) je trouve que arg(z')= arg(-i) + arg(W)
Ensuite pour la question d) c'est comme pour la méthode précédente, je sais que arg(z') = -
mais je ne vois pas en quoi ça me donne l'ensemble (E)
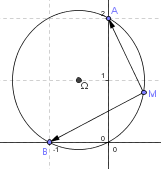
(x+(1/2))²+(y-1)² = 5/4 est l'équation du cercle de centre  (-1/2;1) et de rayon (
(-1/2;1) et de rayon ( 5)/2
5)/2
Pour l'interprétation géométrique , il faut trouver les points M tels =
 /2 ou -
/2 ou - /2
/2
Quel est l'ensemble de ces points ?
bonjour j'ai le meme exercice a faire. Je ne comprend pas comment faire pour Im(z'). Est ce que vous pourriez detaillez la facon d'obtenir le resultat svp
Bonjour Chopin
(On a multiplié numérateur et dénominateur par la quantité conjuguée du dénominateur)
Développe le numérateur avec soin et attention ....( l'erreur se glisse facilement dans ce type de calculs  )
)
On arrive à -ix² - ix + y - iy² -2x - 2 + 2iy pour le numérateur
On regroupe les termes de la partie réelle , et ceux de la partie imaginaire :
-2x + y - 2 + i(-x²-x-y²+2y)
On cherche l'ensemble (E) des points M lorsque M' appartient à l'axe des abscisses ; cela signifie donc que l'image doit être un réel , et en conséquent la partie imaginaire doit être nulle .
Donc ici , on ne s'occupe pas de la partie réelle , la seule condition étant que Im(z') = 0
J'ai reussi merci.
Pour la question 2) c j'arrive à la
arg(z')= arg(-i) + arg(w)
Mais que faire apres
Comme déjà indiqué ,
arg(W) = arg( (z-2i)/(z+1) ) = arg( (z-zA)/(z-zB) ) = , arg(z') = k
 et arg(-i) = -
et arg(-i) = - /2
/2
Inspire-toi de ce qui est écrit plus haut pour positionner les points M
J'ai déja noté cela mais je ne vois pas comment on peut faire pour exprimer arg(z') en fonction de arg(w)
z' doit être réel, donc le point image doit se trouver sur l'axe des réels
L'argument d'un réel est k
On a l'égalité arg(z')= arg(-i) + arg(w) qui permettra d'écrire
k = -
= - /2 +
/2 +
Ainsi =
 /2 + k
/2 + k
En d'autres termes , l'angle doit être un angle droit
Regarde la figure du 08-11-12 à 20:24 pour déterminer l'ensemble de ces points M


