Bonjour

Deux équations et trois inconnues; tu sors une des inconnues de l'équation du premier degré et tu l'injectes dans l'autre.
Par exemple, ici tu peux commencer par x=-2y+z+1...
Mais c'est pas drôle!

Bonjour,
Un cercle dans l'espace ne peut pas être défini par une seule équation.

Bien le bonjour,


Merci pour vos réponses !


Bon j'ai à peine commencé à tenter la résolution du système à deux équations et trois inconnus mais je me suis arrêter devant l'absence de perspective de mes calculs...

Et si comme le dit Sylvieg un cercle dans l'espace ne peut pas être défini par une seule équation alors je me demande bien où va me mener la résolution éventuelle de ce système.

Bonjour,
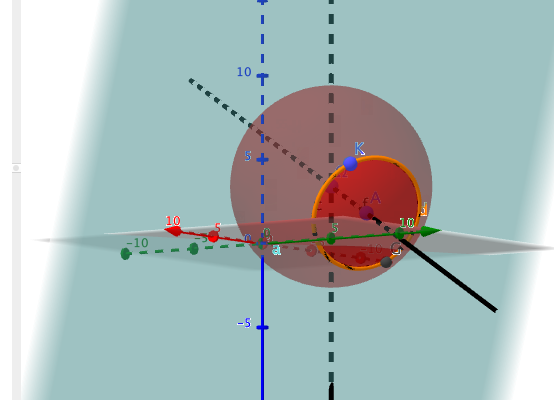
A partir de l'équation du plan P  on obtient  l'équation paramétrique de la perpendiculaire au plan P passant par le centre de la sphère , les coordonnées du centre du cercle  de l'intersection  (-5,4,2)  (plan ,sphère)puis  le rayon du cercle   (2√3).
mais géogébra  donne une équation de ce cercle  mais je ne sais pas la justifier
"X = (-5, 4, 2) + (-3.098 cos(t) - 0.632 sin(t), 1.549 cos(t) - 1.265 sin(t), -3.162 sin(t))"

Ci-dessous, quelques généralités concernant un espace affine euclidien de dimension 3 muni d'une base orthonormée.

Certaines surfaces peut être définies par une équation cartésiennes.
Exemples simples de surfaces : plan et sphères.

Une ligne ne peut être définie par une seule équation cartésienne.
Exemples de ligne : droites et cercles.
Une droite peut être définie comme intersection de deux plans.
Elle peut alors être définie par un système de deux équations cartésiennes correspondant à chacun des plans.
Une droite peut aussi être définie par un système de 3 équations paramétriques.

Bonjour PLSVU,
Je n'avais pas vu ta réponse.
Ta dernière ligne n'est pas une équation cartésienne.
Ça ressemble au début d'un système d'équations paramétrées du cercle.
Bizarres ces virgules. Il devrait y avoir du Y = et du Z =

OUI      M est sur le cercle si
x = -5+ (-3.098 cos(t) - 0.632 sin(t),
y=4+1.549 cos(t) - 1.265 sin(t)
z=2-3.162 sin(t)

si on demande de tracer le cercle en précisant le centre , le rayon et l'axe   geogebra indique
X=( -5,4,2)+ (3.098 cos(t) + 0.632 sin(t), -1.549 cos(t) + 1.265 sin(t),+3.162 sin(t))

D'accord
Je ne suis pas habituée aux notations de géogébra.

Bonjour,


Merci à tous pour vos réponses ! C'est intéressant !


Sylvieg : "Une ligne ne peut être définie par une seule équation cartésienne."

J'ai trouvé cet exemple d'équation cartésienne d'une droite dans l'espace sur internet :
x = 2 y +1 = 3z - 2.
En fait  c'est bien sûr comme vous l'avez dit deux équations cartésiennes correspondantes à 2 plans.
C'est donc quelque chose comme ça que je pourrais obtenir en guise d'équations cartésiennes (que je mets au pluriel du coup) de l'intersection de la sphère et du plan j'imagine.
Si je poussais le calcul, j'aurais 2 équations avec pour chacune 2 variables (Ou doit-on dire 2 inconnues ?).


Merci PLSVU pour avoir donné l'équation paramétrique du cercle.
Je me demande donc si l'on pourrait obtenir cette équation avec seulement les équation de la sphère et du plan et sans passer par le raisonnement géométrique.
Je doute que ce soit possible.

Bonjour,
A partir  de
A=(-5,4,2) centre  de la sphère de rayon 2√3, d'axe ∆(1,2,-1)
on peut en déterminer  les points d'intersection de la sphère  avec le plan P(x+2y-z=1)
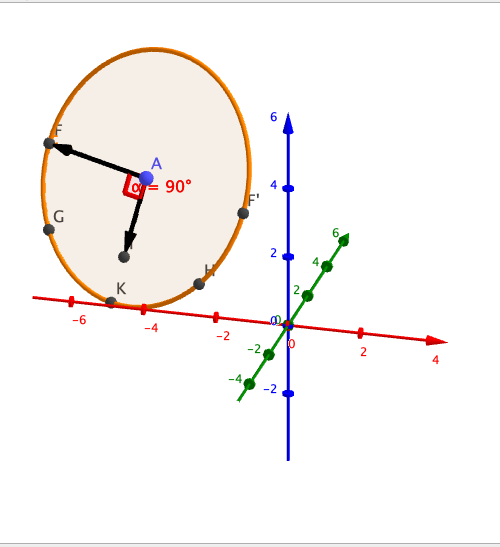
lorsque z=2  on obtient deux points diamétralement opposés  
   F=(-5-2√2.4;4-√2.4; 2)     F'(-5+2√2.4;4+√2.4; 2)
lorsque z=0  on obtient deux points  G  (-3,2,0)  et H(-7,8,4,4,0)
  I milieu du segment [GH]  (-5,4;3,2;0)
\vec{AI}(-0,4,-0,8;-2)
\vec{AF}(-2.\sqrt{2.4;}\sqrt{2,4};0
\vec{AI}\times \vec{AF}=0
les vecteurs sont  donc orthogonaux  dans le plan P
||\vec{AI}||=\dfrac{4\sqrt{3}}{\sqrt{10}}
soit K l'image du point F  dans la rotation d'axe ∆  pour t=π/2
||\vec{AK}||=k ||\vec{AI}|=2\sqrt{3}
k=0,5\sqrt{10}[/tex]


si  le point F  tourne dans le sens anti horaire d 'un angle de mesure   t  son image  M a pour coordonnées
x=-5-2√2,4cos(t)-0,2√10 sin(t)
y=4- √2,4cos(t)- 0,4√10 sin(t)
z=2-√10sin(t)

Bonjour,
A partir  de
A=(-5,4,2) centre  de la sphère de rayon 2?3, d'axe ?(1,2,-1)
on peut en déterminer  les points d'intersection de la sphère  avec le plan P(x+2y-z=1)
lorsque z=2  on obtient deux points diamétralement opposés  
   F=(-5-2?2.4;4-?2.4; 2)     F'(-5+2?2.4;4+?2.4; 2)
lorsque z=0  on obtient deux points  G  (-3,2,0)  et H(-7,8,4,4,0)
  I milieu du segment [GH]  (-5,4;3,2;0)

les vecteurs sont  donc orthogonaux  dans le plan P

soit K l'image du point F  dans la rotation d'axe ?  pour t=?/2



si  le point F  tourne dans le sens anti horaire d 'un angle de mesure   t  son image  M a pour coordonnées
x = -5-22,4cos(t)-0,210 sin(t)
y = 4- 2,4cos(t)- 0,410 sin(t)
z = 2-10sin(t)

_{* Modération >  *Balises LaTeX manquantes ajoutées *}

Bonsoir,
Merci pour les balises  .
je corrige   des erreurs de signes
  Bonjour,
A partir  de
A=(-5,4,2) centre  de la sphère de rayon 23 , d'axe ∆ (1,2,-1)
on peut en déterminer  les points d'intersection de la sphère  avec le plan P(x+2y-z=1)
lorsque z=2  on obtient deux points diamétralement opposés  
   F=(-5-2√2.4;4+√2.4; 2)     F'(-5+2√2.4;4-√2.4; 2)
lorsque z=0  on obtient deux points  G  (-3,2,0)  et H(-7,8;4,4;0)
  I milieu du segment [GH]  (-5,4;3,2;0)

les vecteurs sont  donc orthogonaux  dans le plan P

soit K l'image du point F  dans la rotation d'axe  ∆ pour t=π/2



si  le point F  tourne dans le sens anti horaire d 'un angle de mesure   t  son image  M a pour coordonnées
x = -5-22,4cos(t)-0,210 sin(t)
y = 4+2,4cos(t)- 0,410 sin(t)
z = 2-10sin(t)
  on peut vérifier que

  figure: