Niveau école ingénieur

équation f(x) =1/2

Posté par
nano80 06-09-17 à 16:34

Bonjour à tous,

Voici un autre exercice si quelqu'un peut me corriger svp. je vous remercie par avance

On considère l'expression :
f(x) = cos²x - cos²2x + cos x cos 3x
Montrer que cette expression peut s'exprimer très simplement en fonction de cos2x. Résoudre alors l'équation f(x) =1/2 et représenter sur le cercle trigonométrique les solution de cette équation.
f(x) = cos²x - cos²2x + cos x cos 3x

f(x) = cos²x - cos²2x + cos x cos 3x
= (cos ²x + cosx cos3x) - cos ²2x
= cosx (cosx+cos 3x) - cos ²2x
= [ cos x (2cos 4x/2 *cos 2x/2)] - cos² 2x
= 2cos x*cos 2x*cosx - cos ²2x
= 2cos²x*cos 2x - cos ² 2x

Or cos 2x = 2cos ²x -1 ou 2cos ²x = cos 2x +1

=>
=(cos 2x +1)*cos 2x - cos ²2x
=cos ²2x + cos 2x - cos ²2x
= cos 2x

2) On résout f(x)=1/2
Soit
cos(2x)=1/2

Equivalant à :
Cos(2x) = cos (π/3) ou = cos ((-π)/3) ou =cos(5π/3) ou = cos((-5π)/3)
Ce qui nous donne bien 4 solutions dans ]-pi;pi]

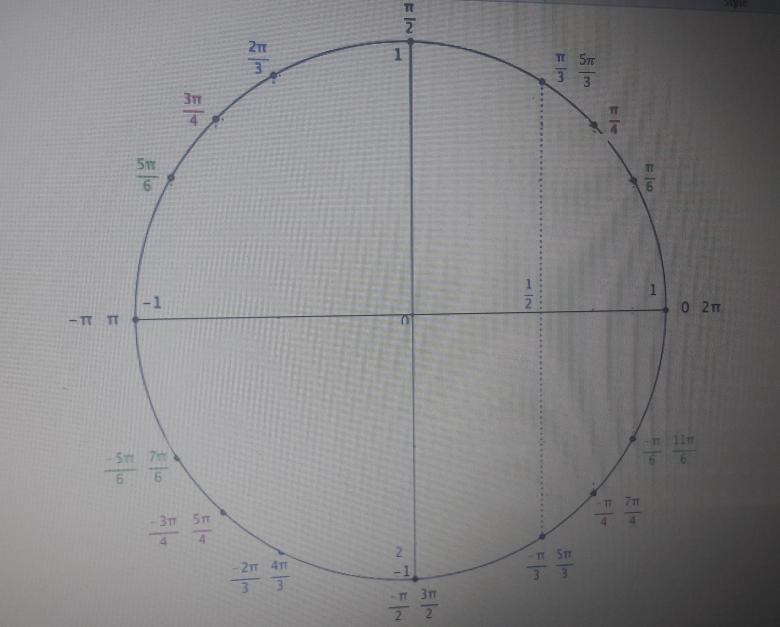
équation f(x) =1/2

Posté par re : équation f(x) =1/2 06-09-17 à 17:34

bonjour,
cos(2x)=1/2 équivalent à 2x= $\pi/3+2k\pi$ ou $2x=-\pi/3+2k\pi$
donc $x=\pi/6+k\pi$ ou $x=-\pi/6 +kpi$
ce qui donne dans $]-\pi,\pi]$
$\pi/6; -\pi/6;5\pi/6;-5\pi/6$

Posté par re : équation f(x) =1/2 06-09-17 à 18:26

ok DOMEREA.....tu as tout à fait raison ...merci beaucoup.

Posté par re : équation f(x) =1/2 06-09-17 à 18:52

nano80 @ 06-09-2017 à 16:34

cos(2x)=1/2

Equivalant à :
Cos(2x) = cos (π/3) ou = cos ((-π)/3) ou =cos(5π/3) ou = cos((-5π)/3)
Ce qui nous donne bien 4 solutions dans ]-pi;pi]

Bonjour,
Il faut y aller par étapes.
étape 1: Se débarasser du $\cos$

$\cos 2x=\frac{1}{2}\Leftrightarrow 2x= \pm \dfrac{\pi }{3}+2k\pi ;k\in\mathbb{Z}\Leftrightarrow x= \pm \dfrac{\pi }{6}+k\pi ;k\in\mathbb{Z}$

étape 2: Cherchons toutes les solutions tel que $x\in]-\pi,\pi[$

$\cos 2x=\frac{1}{2}\Leftrightarrow 2x= \pm \frac{\pi }{3}+2k\pi ;k\in\mathbb{Z}\Leftrightarrow x= \pm \frac{\pi }{6}+k\pi ;k\in\mathbb{Z}$

a) $x= \frac{\pi }{6}+k\pi ;k\in\mathbb{Z}$
$-\pi < x\leqslant \pi \Leftrightarrow -\pi < \frac{\pi }{6}+k\pi\leqslant \pi \Rightarrow -\frac{7}{6}< k\leqslant \frac{5}{6}\Rightarrow k=0$ ou $k=-1$ Donc: $x=\frac{\pi }{6} ou x=-\frac{5\pi }{6}$

b) $x= -\frac{\pi }{6}+k\pi ;k\in\mathbb{Z}$
$-\pi < x\leqslant \pi \Leftrightarrow -\pi < -\frac{\pi }{6}+k\pi\leqslant \pi \Rightarrow -\frac{5}{6}< k\leqslant \frac{7}{6}\Rightarrow k=0$ ou $k=1$ Donc: $x=-\frac{\pi }{6} ou x=\frac{5\pi }{6}$

Donc, nous avons 4 solutions dans $]-\pi,\pi[$ qui sont: $\left \{ -\frac{5\pi }{6},-\frac{\pi }{6},\frac{\pi }{6},\frac{5\pi }{6} \right \}$

Posté par re : équation f(x) =1/2 06-09-17 à 19:02

Très claire Razes..merci