Inscription / Connexion Nouveau Sujet
Espace : détermination d'une équation et projeté orthogonal
Bonjour.
Je dois faire une annale concernant la géométrie dans l'espace et je bloque sur les dernières questions. Pouvez vous m'aider? Merci d'avance.
L'espace est muni d'un repère orthonormal (O, 
,
, 
).
Soit (P1) le plan d'équation cartésienne -2x+y+z-6=0
Soit (P2) le plan d'équation cartésienne x-2y+4z-9=0
1. Montrer que (P1) et (P2) sont perpendiculaires.
-> Pas de soucis
2. Soit (D) la droite d'intersection de (P1) et de (P2). Montrer qu'une représentation paramétrique de (D) est:
x=-7+2t
y=-8+3t avec t
z=t
-> J'ai également réussi à le démontrer
3. Soit M un point quelconque de (D) de paramètre t et soit A le point de coordonnées (-9 ; -4 ; -1).
a. Vérifier que A n'appartient ni à (P1), ni à (P2)
-> Juste en remplaçant on y arrive
b. Exprimer AM² en fonction de t.
-> C'est fait grâce à la formule de la distance. Je trouve:
14t²-14t+21
3. Soit f la fonction définie sur |R par f(t) = 2t²-2t+3
-Étudier les variations de f -> Sans soucis. La fonction f est décroissante de -
à 1/2 puis croissante de 1/2 à +
-Pour quel point M, la distance AM est-elle minimale ?
Dans la suite, on désignera ce point par I.
-> Un peu plus de mal pour cette question. Je ne sais pas si j'en ai le droit mais j'ai dit que comme AM²=7f(t), alors la distance AM est minimale lorsque la fonction f(t) admet son minimum.
J'ai donc remplacé t par 1/2 dans l'équation paramétrique. Ce qui nous donne I(-6 ; -13/2 ; 1/2)
-Préciser les coordonnées du point I.
-> Voir ci dessus
4. Soit (Q) le plan orthogonal a (D) passant par A.
a. Déterminer une équation de (Q)
-> Sur cette question je suis bloquée car je pense qu'il faudrait se servir du vecteur directeur 
de la droite (D) qui doit être colinéaire au vecteur normal n du plan (Q). On connait (2 ; 3 ; 1) mais je ne sais pas comment faire ensuite..
b. Démontrer que I est le projeté orthogonal de A sur (D)
-> Ici je n'ai même pas d'idée de départ
4/
2(x+9)+3(y+4)+1(z+1)=0
traduit que Q passe par A et est normal à D
Il suffit de dire que A est sur D est aussi dans Q
puisque D et Q sont orthogonaux par construction
4/
2(x+9)+3(y+4)+1(z+1)=0
traduit que Q passe par A et est normal à D
petite correction
Il suffit de dire que I est sur D est aussi dans Q
puisque D et Q sont orthogonaux par construction
D'accord mais je ne comprends pas pourquoi l'équation que vous proposez traduit le fait que Q passe par A et est normal à D ? 
oh !
1/ remplace x, y, z par les coordonnées de A. obtiens-tu 0=0 ?
2/ quel est le vecteur normal au plan que je propose ? est-ce un vecteur directeur de D ?
encore une question ? 
En effet on trouve bien 0=0 et c'est un vecteur directeur de D. Mais comment avez vous trouvé cette équation ?
mais j'ai fait en sorte que...
dans un repère orthonormé :
une équation du plan normal à de coordonnées
et passant par A de coordonnées
est
cette équation satisfait aux deux conditions citées; c'est tout.
si tu la développes, tu auras
tu choisis de retenir celle qui te convient le mieux. Moi, je trouve que la première est plus "parlante", donc plus facile à mémoriser.
Ah d'accord avec cette propriété ca va mieux
Mais je ne la trouve pas dans mon cours! Merci
Pour la 5 ai-je droit à une piste ? 
Mais je ne la trouve pas dans mon cours
regarde mieux : cette relation est la conséquence directe du produit scalaire nul de deux vecteurs orthogonaux.
de coordonnées
A de coordonnées
M de coordonnées (x;y;z)
alors de coordonnées
le plan passant par A perpendiculaire à la droite de vecteur est tel que :
tu retrouves la formule que j'ai utilisée.
Pour la 5 ai-je droit à une piste ?
peut-être
mais je n'ai pas vu de point n° 5 dans ton premier message
le plan et la droite sont déjà perpendiculaires, on les a construit pour ça;
I est le point du plan qui est à la distance la plus courte de A
il te suffit de vérifier que I est aussi sur la droite.
Cet exercice veut illustrer le fait que la distance la plus courte d'un point à un plan est celle qui sépare ce point de son projeté orthogonal (ici, I) sur le plan.
mais tu connais, ou tu devrais connaître l'équivalent vu en Première de la distance d'un point à une droite dans le plan : cette distance est aussi celle qui sépare le point de son projeté orthogonal sur la droite.
Est-ce que tu vois l'équivalence entre les deux situations ?
J'ai fait un dessin pour essayer de mieux comprendre mais j'ai du mal.
Quand vous dites "il te suffit de vérifier que I est aussi sur la droite", parlez vous de la droite (D) (car ça on le sait déjà d'après l'énoncé) ou de la droite (AI)?
Si je calcule grâce à la formule la distance entre le point A et la droite (D), que m'indique mon résultat. Faudrait il que je calcule aussi la distance AI à l'aide des coordonnées des points et que celles ci soient similaires?
Cependant je ne pense pas que cela suffise à démontrer que I est le projeté orthogonal. Si?
Ok, j'ai relu ton énoncé, et je fais le point ci dessous
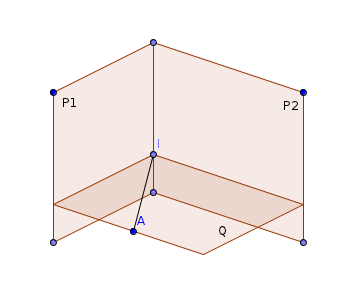
P1 et P2 se coupent en D
A extérieur à P1 ou P2
I est sur D, tu as raison
I a été choisi pour que la distance AI soit la plus petite distance de A à la droite D
mais on n'a pas démontré encore que AI est orthogonal à D (même si un résultat général l'annonce, on feint ici de l'ignorer pour mieux le redécouvrir)
alors on construit le plan Q qui passe par A et qui est perpendiculaire à D
et il reste à montrer que I appartient bien à Q, ce qui démontrera que (AI) est effectivement perpendiculaire à D
Q a pour équation 2x+3y+z+31 = 0
I a pour coordonnées (-6;-13/2;1/2)
quand on remplace (x;y;z) par (-6;-13/2;1/2) dans l'équation 2x+3y+z+31 = 0 de Q, on trouve bien 0=0
D'accord merci beaucoup pour ce dessin façon informatique c'est beaucoup plus clair.
Une dernière chose: J'ai bien compris qu'il fallait démontrer que (AI) était orthogonal à (D) et comment le démontrer mais cela suffit il à répondre à la question? (tout en précisant que I appartient par construction à la droite D)
Merci
C'est là que ça rejoint ce que je disais précédemment :
si tu vérifies simplement que I appartient au plan Q, alors tu auras montré que (AI) est perpendiculaire à D.
Le plan Q est le plan perpendiculaire à D, donc toutes les droites du plan Q sont perpendiculaires à D
si tu montres que I appartient à Q, alors la droite (AI) appartient à Q, et donc est perpendiculaire à D.
Si tu veux te rassurer, tu peux aussi calculer les coordonnées du vecteur et montrer qu'il est
à ton vecteur directeur de D, mais cette solution, quoique correcte, est moins élégante à mon avis.
tu peux rédiger les deux solutions en indiquant clairement qu'il suffit d'une seule d'entre elles pour affirmer le résultat. Cette démarche peut aussi être très appréciée de ton correcteur.
Annuler
connectez vous