Inscription / Connexion Nouveau Sujet
Etude d'une fonction définie grace d'un radical
Bonjour à tous
j'ai un exercice à faire pour la rentrée (qui approche malheureusement beaucoup trop vite à mon gout
) et j'ai des difficultésà le comprendre.
voici l'énoncé:
f est la fonction définie sur l'intervalle I=]-1;1] par f(x)=
((1-x)/1+x))
On note C la courbe représentative de f dans un repère orthonormal.
I)Etude de la dérivabilité de la fonction f
1a. Démontrer que la fonction f est dérivable sur l'intervalle ]-1;1].
Ici je suppose que -1 est exclu car on ne peut pas diviser par 0
b. Démontrer que pour tout réel x de ]-1;1], f'(x)=(-1/(1+X)²)(1+x/1-x)
2)
a. Démontrer que pour tout réel h tel que -1<1+h<1, (f(1+h)-f(1)/h)=--1/h(2+h)
b. Calculer la limite de f(1+h)-f(1)/h lorsque h tend vers 0. Interpréter graphiquement le résultat obtenu. La fonction f est-elle dérivable en 1?
II)Etude des variations de la fonction f
a. Calculer la limite de f en -1. Etudier le sens de variation de f.
b. Dresser le tableau de variation de la fonction f.
III) Construction de la courbe C
a. Déterminer une équation de la tangente T à la courbe C au point d'abscisse 0.
b. Justifier que la courbe C admet une asymptote verticale 
c. Construire la courbe C, les droites , T et la tangente à C au point
d'abscisse I.
J'ai vraiment des difficultés avec les fonctions et leur limites ainsi que leur dérivabilité, je n'arrive absolument pas à comprendre cet exercice. Je vous remercie beaucoup si vous pouvez m'apporter de l'aide.
Sur ce bonne journée à vous
bonjour à tous!!
s'il vous plait, pourriez vous m'aider? je n'arrive pas à me sortir de cet exercice. je vous serai très reconnaissant de m'aider
tout d'abord excuse moi pour mon comportement, je me suis rendu compte que je passe pour le feignant qui veut que les autres fassent son dm. excuse moi encore
Pour le 1)a) 1 est exclu car on ne peut pas diviser par 1. La fonction n'est dérivable qu'entre -1 et 1 car il y a la racine. mon raisonnement est-il bon?
pour la 1)b) je dérive la fonction comme si il s'agit d'une composée. je commence donc par dériver 1-x/1+x mais je trouve -2/(1+x)² car je fais -1-x-1+x/(1+x)². pourrais-tu m'aider?
Pour la 1) tu dois avoir des théorèmes dans ton cours sur la dérivation d'un quotient, d'une composée. Pas facile à rédiger c'est vrai.
Pour 2)
En posant u(x) = (1-x)/(1+x) on a effectivement u'(x) = -2/(1+x)²
or
donc
En simplifiant par 2 on obtient le résultat escompté.
...
ok donc j'étais bien parti, merci beaucoup pour ce résultat. En ce qui concerne la 2a)j'ai un problème car lorsque je remplace les x par f(1+h) j'arrive à trouver h/2+h. Malheuresement notre prof ne nous a pas expliquer comment faire lorsqu'il y a des f(h) et les cours de première sont bien loin donc je ne retrouve pas comment faire autrement...
En revanche pour la limite quand h tend vers 0 j'ai trouvé que la limite est 1 car je remplace h par 0 dans l'expression --1/h(2+h). Donc la fonction n'est pas dérivable en 1. Est-ce juste?
et on obtient le résultat attendu.
Par ailleurs ta conclusion n'est pas cohérente : si tu trouves comme limite 1, tu devrais conclure à la dérivabilité en 1 (à gauche), et un nombre dérivé (à gauche) égal à 1. Mias on ne trouve pas 1 comme limite.
ci-dessous la situation vue par s"inequanon"
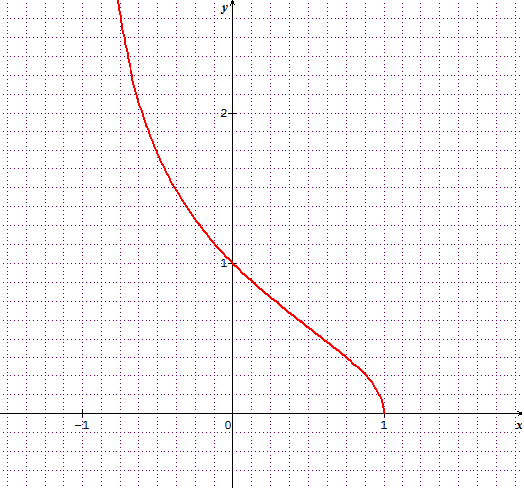
Si j'ai bien compris je dois donc dire que la fonction est dérivable en 1 mais que la limite n'est pas 1? parce que je n'arrive pas à comprendre pourquoi on devrait trouver un nombre dérivé égal à 1.
Non, tu n'as pas bien compris; relis avec attention mon post précédent.
La limite n'est pas 1 ; et même si elle était égale à 1 ta conclusion de 17:35 ne serait alors pas cohérente.
donc la limite en 1 est 0 car on voit qu'elle tend vers 0, par conséquent la fonction est dérivable en 1?
non.
f est dérivable en 1 si a une limite finie lorsque h tend vers 0.
Ce qui n'est pas le cas ici.
.
ok d'accord merci beuaucoup. pour la 2a) j'ai trouvé que la limite en -1 est + l'infini car ca donne 2. Est-ce juste?? ensuite si mon résultat est juste je pense réussir à faire le tableau de variation. En revanche je n'arrive pas à déterminer l'equation de la tangente car le prof nous fait réviser en meme temps que cet exercice dc je n'arrive plus à appliquer les formules...
pour la 2a) j'ai trouvé que la limite en -1 est + l'infini car ca donne
2
Je ne comprends pas le "car"
?
en fait j'ai calculé za-zc/zg-zc et le résultat est 2 (d'après mes calculs
) j'en ai conclu que la limite est +
en -1
ok donc j'ai fait: (1-(-1)/1+(-1))=(2/0)+2
oups a la fin c'est un = et non pas un +
pourrais-tu me dire si ce calcul est juste stp?
Bonjour
Voila , je suis actuellement entrain de faire ce même exercice .
J'essaye de répondre à la question 2 b , selon moi elle n'admet pas de limite determiné mais pourquoi nous demande-t-on de calculer sa limite alors ? dans ce cas elle ne serait pas dérivable en 1
Si vous pouviez m'aidez ?? s'il vous plaît
On obtient - lorsque h tend vers 0 par valeurs inférieures à 0.
La conclusion vient alors toute seule.
Je suis actuellement sur cette exercice, et je souhaiterais qu'on m'éclaircisse l'esprit notamment pour le 1)a ou je bloque considérablement. Merci à vous
Bonsoir,
est-ce-qu'il n'y aurais pas d'erreur sur l'enoncé car pour l'ensemble de derivabilité j'ai trouvé ]-1;1[.
Annuler
connectez vous