Inscription / Connexion Nouveau Sujet
etude d'une fonction impaire
bonejour j'ai besoin d'aide pour cet exercice! s'il vous plait!
f définie sur IR par
f(x)= (x+1)-2e^(x)/(e^(x)+1)
1) demontrer que que f est impaire,c'est à dire que pour tout réel x, f(-x)=-f(x)
que peut on deduire pour la courbe c?
2)
a) démontrer que pour tout réel x, f(x)=(x+1)-2/(1+e(-x))
b) en déduire la limite de f en +
3) a) démontrer que pour tout réel x, on a
f(x)-(x-1)= 2/(e(x)+1
b) en déduire que la droite 
d'équation y=x-1 est asymptote à c en +
c) préciser la position de c par rapport à
4) etudier les variations de f sur ) 0, +(
5) tracer la courbe c, la tangente à c au point o, et les asymptotes et ' ( on remarquera que c admet une asymptote ' en +)
merci d'avance! au revoir
Une courbe impaire est symétrique..
Représente toi -f(x)=f(-x) sur un schéma pour essayer de trouver par rapport à quoi.
Hello Rosie,
ce qui serait intéressant c'est de savoir ce que tu as réussi à faire dans cet exercice.
Okay....donc
3)
a)
tu réduis au même dénominateur
et tu trouves.
b)
en utilisant la question a) on trouve ce qui prouve que
est assymptote en
En outre comme la courbe est toujours au-dessus.
4)
je te laisse faire les calculs et réduire au même dénominateur, à la fin on trouve
.
Comme la fonction est croissante.
5)
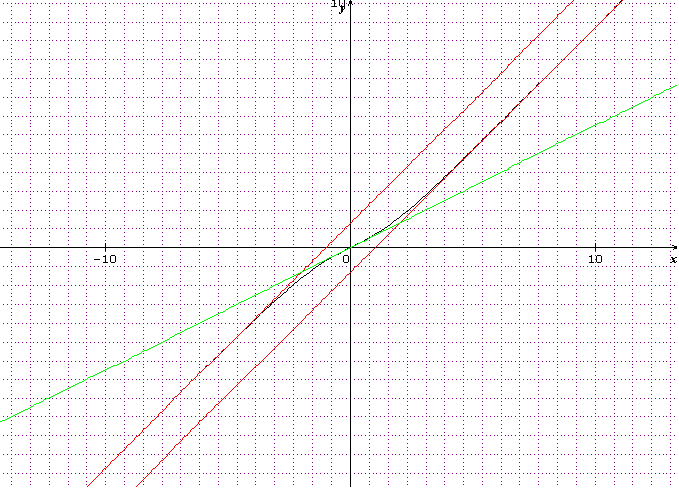
j'ai fait f'(x)= 1-2e^x(e^x+1)²-2e^x(e^x+1)-2e^2x/ (e^x+1)² pour le mettre au meme denominateur j'ai trouve
f'(x)= e^2x+2e^(x)+1-2e^2x-2e^x-2e^2x/(e^x+1)²
et j'ai trouvé f'(x)= -3e^2x+1/(e^x+1)²
est ce que cela est juste?
.
Annuler
connectez vous