Inscription / Connexion Nouveau Sujet
Etude de dérivabilité
Bonjour, voila j'ai problème sur cet exercice :
On considère la fonction f définie sur [-1;1] par : f(x) = (1-x) (x^2-x^4) . On note C sa courbe.
(x^2-x^4) . On note C sa courbe.
Partie A - Etude de la dérivabilité en -1
1.Exprimer f(-1+h)-f(-1)/h en fonction de h, avec h>0.
2.Calculer lim h 0+ f(-1+h)-f(-1)/h. Qu'en déduit-on ?
0+ f(-1+h)-f(-1)/h. Qu'en déduit-on ?
Partie B - Etude de la dérivabilité en 1
1.Exprimer f(1+h)-f(1)/h en fonction de h, avec h<0.
2.Calculer lim h 0- f(1+h)-f(1)/h . Qu'en déduit-on ?
0- f(1+h)-f(1)/h . Qu'en déduit-on ?
Partie C - Etude de la dérivabilité en 0
1.Exprimer f(h)-f(0)/h-0 en fonction de h avec h>0 .
2.Calculer lim h 0+ f(h)-f(0)/h-0 .
0+ f(h)-f(0)/h-0 .
3.Exprimer en fonction de h avec h<0 .
4.Calculer lim h 0- f(h)-f(0)/h-0.
0- f(h)-f(0)/h-0.
5.Qu'en déduit-on ?
Donc moi se que j'ai fait c'ets que j'ia remplacé dans f(x) x par 1+h et à la fin j'obtiens:
((2-h)valeur absolue -1+h valeur absolue  (h(2-h))/h
(h(2-h))/h
Mais j'ai de gros doute , vous en pensez quoi ?
et bien j'ai fait toute les parties mais je ne suis pas sur de mes calculs donc en faite je pense que si la partie A est bonne les autres seront bonnes aussi.
A la partie A j'ai trouvé ceci :
1) f(-1+h)-(-1) / h = (2-h)|-1+h| (h(2-h))
(h(2-h))
2) lim 2-h =2
lim |-1+h|=-1
lim h(2-h) = 0
Donc lim (-1+h)-(-1) / h =+
et Donc la fonction n'est pas dérivable a droite en -1
Vous en pensez quoi ?
A.
Je trouve :
La présence du 2/h fait que cette expression tend vers + : f n'est pas dérivable en -1.
: f n'est pas dérivable en -1.
B.
Les deux premiers termes tendent vers 1, donc, la limite de ce rapport en 0 est égale à la limite de |h|/h
Ce sera -1 pour h tendant vers 0 par valeurs inférieures et 1 pour h tendant vers 0 par valeurs supérieures .
Deux limites différentes : f n'est pas dérivable en 0.
D'accord donc en résumé la fonction n'est pas dérivable ne -1, ni en 1 ni en 0 si j'ai bien tout suivie ?
Il reste le cas x tend vers 1 par valeurs inférieures. Je pose x = 1-h, h > 0
Cette expression tend vers 0 : f est dérivable en 0.
Je ne comprend pas pourquoi vous étudiez le cas lorsque x tend vers 1, car a chaque fois on nous demande lorsque x tend vers 0+ ou 0-
On te demande bien la dérivabilité en x = 1 ?
Je reconnaîs que je me suis trompé dans la numérotation des questions, c'est peut-être pour cela que tu ne vois pas ce que j'ai fait.
Tu as raison : j'ai fait une faute de frappe indécente :
"Cette expression tend vers 0 : f est dérivable en 0."
est à remplacer par :
"Cette expression tend vers 0 : f est dérivable en 1."
et on peut rajouter : f '(1) = 0
D'accord tres bien 
Juste une dernière question qui concerne la partie D
Partie D
1.a) Soit x € ]-1;1[ - {0}. Calculer f'(x) .
b)Montrer : f'(x) = (3x^4-2x^3-2x^2+x )/  (x^2-x^4).
(x^2-x^4).
c)Factoriser le numérateur de f'(x) en un produit de polynômes de degrés 1 ou 2.
d)Etudier les variations de f et dresser son tableau de variations.
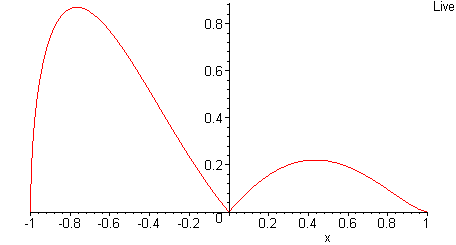
2.Le plan est muni d'un repère orthonormal d'unité graphique 5 cm.
On note D et D' les droites d'équations y=x et y=-x .
Tracer C, D et D'. Que peut-on dire des droites D et D' ?
Ma pose question se porte pour la factorisation en un produit de polynômes, dois-je faire une division d' equation par x^2 ?
Car je ne trouve rien de bien en plus par rapport a la question d'après, étudier les variations je pense que cela pourrait m'aider pour remplir le tableau , qu'est ce que vous en pensez ?
Je te laisse finir la factorisation.
Les deux droites y = -x et y = x représentent les deux demi-tangentes au point 0.
Donc pour la factorisation j'obtiens x[(x-1)(3x^2+x-1)]
Mais finalement je me demande si cela va me servir pour le tableau de variations ?
D'accord très bien merci j'ai terminé, jvous remercie pour tout et jvous teindrais au courant de la note que j'ai eut si sa vous intéresse .  encore une grand merci
encore une grand merci
Bonne après midi


