Inscription / Connexion Nouveau Sujet
Etudier le signe d'une expression
Bonjour
Si on me demande d'étudier le signe d'une expression, je vais dire f(x) = .......
c'est une égalité, je ne suis pas obligée là, de faire un tableau de signes ?
Merci 
Bonjour,
tout dépend de la forme de l'expression qu'on te donne à étusier...
as-tu un exemple précis ?
Bonjour Tilk 
oui, je te montre mon expression :
f(x) = (x - 2)² - 9 - (x + 1)(2x - 3)
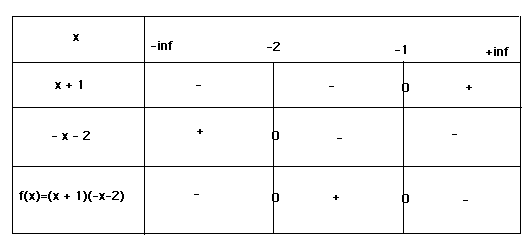
j'ai trouvé f(x) = (x + 1)(-x - 2)
puis j'ai résolu f(x) = 0
ce qui me donne x = - 1 ou x = -2
pas besoin de tableau dans ce cas là ?
Merci 
Bonjour littleguy
mais pourquoi donc ?
je vais me retrouver avec des intervalles - 0 + 0 - et j'en fais quoi ?
> Louisa
La question est
étudier le signe
- si x ... alors ...
- si x ... alors ...
Bonjour liitleguy 
Louisa tu écris :
je vais me retrouver avec des intervalles - 0 + 0 - et j'en fais quoi ?
comment as-tu procédé pour en arriver là ?
pour étudier le signe de l'expression (x+1)(-x-2) il faut faire un tableau de signes..
tu devrais constater que cette expression est positive sur l'intervalle [-2;-1] et négative ailleurs...
Bonsoir tout le monde
Louisa >>
pourquoi tu veux pas faire de tableau ?
tu pourrais t'en passer pour un seul facteur et encore ça gênerait pas
soit à étudier le signe de (x+1)
(x+1) > 0  x > -1
x > -1
(x+1) positif de -1 à l'infini x [-1;
[-1; [
[
(x+1) = 0 pour x = -1
(x+1) négatif de -l'infini à -1 x ]-
]- ;-1[
;-1[
mais à partir du moment où tu as plusieurs facteurs
je te conseille fortement de passer par le tableau de signes.
Bonsoir à tous 
Excusez-moi ! Je n'étais pas libre cet après-midi.
Tilk
comment as-tu procédé pour en arriver là ?
Alors voilà comment j'ai fait :
f(x) = (x - 2)² - 9 - (x + 1)(2x - 3)
f(x) = (x - 2 - 3)(x - 2 + 3) - (x + 1)(2x - 3)
f(x) = (x - 5)(x + 1) - (x + 1)(2x - 3)
f(x) = (x + 1)[(x -5) - (2x - 3)]
f(x) = (x + 1)(x - 5 - 2x + 3)
f(x) = (x + 1)(- x - 2)
J'ai résolu l'équation f(x) = 0
(x + 1)(- x - 2) = 0
Produit de facteur nul.
(x + 1) = 0 ; x = - 1
ou
(- x - 2) = 0 ; x = -2
J'ai donc mes intervalles :
]- inf ; -2[ ; ]- 2; -1[ et ]-1 ; + inf[
f(x) = (x + 1)(- x - 2)
négative sur ]-inf ; - 2[
Positive sur ]-2 ; - 1[
négative sur ]-1 ; + inf[
mais comme je sais que f(x) = 0 pour x = - 2 ou x = - 1
Ben je ne comprends plus comment trouver le signe alors !
Puisque c'est négatif sur tel ou tel intervalle et positif sur un autre

Merci
Ah ! Mais je regarde ta réponse aussi à l'instant littleguy 
Mais plusieurs solutions ne me donnent pas non plus le signe de f(x) ?
Pouh ! Je pige pas grand-chose 
ok ! Daniel aussi !
Mais je n'ai pas fait de tableau moi ?
J'ai vu comme ça ! Mince !
Je dois faire absolument un tableau donc ?
c'est quand même mieux de le faire
il y a moins de risque d'erreur
sinon c'est du bidouillage
pour x=0 qui est dans l'intervalle ]-1;+ inf[
f(x) est négatif, ensuite tu inverses le signe à chaque intervalle.
je doute que l'énoncé te demandes de déduire le signe sans faire de tableau.
sinon c'est du bidouillage

Tu doutes ?????

Il est écrit :
Etudier le signe de f(x) = (x - 2)² - 9 - (x + 1)(2x - 3)
STOP ! RIEN DE +
et bien pour étudier le signe d'une expression
comme je t'ai toujours dit
tu factorises l'expression
et tu fait un tableau des ignes
tu auras pour chaque intervalle le signe de l'expression
Pour Tilk
tu devrais constater que cette expression est positive sur l'intervalle [-2;-1] et négative ailleurs...
Pourquoi [-2 ; - 1[ ?
Je veux dire pourquoi tu fermes le crochet ?
Merci
expression négative sur ]-inf;- 2]
expression strictement négative sur ]-inf;- 2[
zéro peut être aussi bien négatif que positif
il y a une différence entre positif et strictement positif
Mais qui dit que c'est supérieur ou égal à 0 ?
là on te demande seulement d'étudier le signe de l'expression
tu peux inclure f(x)=0 dans l'intervalle
mais quand tu dois dois résoudre une inégalité
du genre f(x) 0 ou f(x)>0
0 ou f(x)>0
tu dois en tenir compte, et inclure ou pas les zéros de l'expression.
Pour x  ]-inf ; - 2[
]-inf ; - 2[  ]- 1 ; + inf[ , f(x) < 0
]- 1 ; + inf[ , f(x) < 0
Pour x  [- 2 ; -1] , f(x)
[- 2 ; -1] , f(x)  0
0
Pour x = - 2 et x = - 1 , f(x) = 0
c'est bon ?
je suis d'accord
Pour x ]-inf ; - 2]  [- 1 ; + inf[ , f(x)
[- 1 ; + inf[ , f(x)  0
0
Pour x ]- 2 ; -1[ , f(x) > 0
est possible aussi
tu met le zéro si tu met l'égalité, donc avec crochet fermé
ou tu l'exclus avec crochet ouvert si tu ne met pas l'égalité
rien n'empêche de le mettre partout:
pour x  ]-inf;-2]
]-inf;-2]  [- 1;+inf[
[- 1;+inf[  f(x)
f(x)  0
0
pour x [-2;-1]
[-2;-1]  f(x)
f(x)  0
0
tu met le zéro si tu met l'égalité, donc avec crochet fermé
je mets le 0 si je mets l'égalité ? il faut d'abord que ça passe par mes pieds pour remonter lentement au cerveau

je parle de l'égalité dans l'inégalité f(x) 0 ou encore dans f(x)
0 ou encore dans f(x) 0
0
au lieu de l'inégalité stricte f(x)>0 ou f(x)<0
pourquoi choisir un intervalle plutôt qu'un autre pour inclure f(x)=0 ?
pourquoi choisir un intervalle plutôt qu'un autre pour inclure f(x)=0 ?
Je ne sais pas moi !
Alors on met l'égalité partout ? C'est possible ?
Merci pour tout et à vous tous

Ok ! C'était tout de même juste alors ! Si je n'avais pas demandé, mon exercice était tout résolu convenablement !
Merci 
Bonjour
J'y reviens encore, je n'arrivais pas à finaliser cet exercice puisqu'on demande d'étudier LE signe
mais pas LES signes, voilà ! Un petit détail qui m'a perturbée !

Bonjour Louisa
il faut le prendre dans le sens que l'expression
pour une valeur donnée de x a un signe bien précis
et un seul à la fois.
ce signe variant en fonction de x
toute l'étude consiste à déterminer le ou les intervalles
des valeurs de x pour lesquelles le signe de l'expression
ne change pas.
Bonjour Daniel
Oui maintenant je vais le savoir, mais je suis restée bloquée sur ce "LE" c'est bête !
Merci et bon dimanche