Inscription / Connexion Nouveau Sujet
Ex.2. Geometrie Dans L'espace et Fonction
Bonjour, j'ai déjà poster un topic pour le première Exercice de mon DM. Mais je n'arrive pas le 2 non plus, on va dire que je n'aime pas trop les fonction.. :p
Énoncé:
ABCDEFGH est un parallélépipède rectangle tel que AB=6, AE=4, et BC=5 cm.
Un point S choisi sur [AE] permet de définir deux pyramides:
•SABCD de sommet S et de hauteur SA.
•SEFH de sommet S et de hauteur SE.
1) Compléter la figure si contre.
- ( je n'est pas de quoi poster une image.)
2) Posons x=AS et notons f(x) le volume de SABCD en fonction de x et g(x) celui SEFH (en cm3).
a)Donner l'ensemble de définition de f puis l'expression algébrique de f(x).
b)Donner l'ensemble de définition de g puis l'expression algébrique de g(x).
c)Quel type de fonctions obtient-on ? Tracer la courbe représentative de f et g dans un même repère.
3) Déterminer pas le calcul la valeur de x pour laquelle les deux pyramides ont le même volume. Verifier sur le graphique.
4) Determiner par le calcul les valeurs de x pour lesquelles le volume de SABCD est supérieur au tiers du volume de SEFH.
Merci de votre aide ! 
Merci, je sais comment poster une image mais je n'ais pas de quoi scanner le DM ou encore reproduire le pavé avec un logiciel..
Cordialement.
Bonjour.
Pour les questions 2a et 2b.
L'enssemble de définition d'une fonction correspond à l'enssemble des valeurs que peux prendre x, on cherche les valeurs de x telles que la fonction décrite existe.
Dans l'énoncé de la question on te dis que x = AS, donc il te suffit de connaitre quelle sont les valeurs possible de AS.
Dans l'énoncé de l'exercice on te dit que S est un point choisit sur AE et que AE = 4.
A partir de là tu peux en déduire quelle sont les valeures possible de x.
Pour les expressions alégébrique on te dit que f et g représente le volume de 2 pyramides donc f(x) = volume SABCD et g(x)= le volume SEFH. Or le volume d'une pyramide est v = 1/3 
Base Hauteur.
Dans l'énoncé on te donne la hauteur et à partir de la tu peux savoir quelle est la base (tu peux t'aider de ton dessin).
Ensuite tu peux en déduire les expressions algébriques des 2 fonctions.
Merci beaucoup pour la reponce.
Pour la a je ne pensais pas faire comme ca mais ca m'est revenu de apres.Je fait tout les calculs et je redis ça après.
NI-Ic0 >>> Merci, je sais comment poster une image mais je n'ais pas de quoi scanner le DM
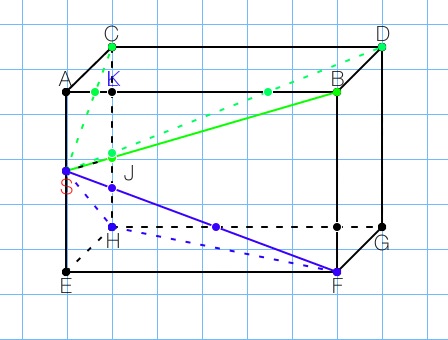
Il n'est pas demandé de scanner le DM mais de faire un schéma (avec GeoGebra par exemple) et de le poster pour éviter que ce soit nous qui voulons t'aider à avoir à le faire .
C'est mieux avec ce schéma bien qu'il y ait des points d'intersection marqués mais qui ne sont pas des intersections comme J , K et quelques autres sans étiquette .
2) Donc en fait l'ensemble de définition est D= [0;4] ?!
2) Je suis d'accord mais comment trouver l'enssemble de définition de f et de g sans connaître f(x) et g(x) ?!
Bonjour
fm_31 je ne comprends pas ce que tu racontes, l'ensemble de définition de f et de g est bel et bien l'ensemble des valeurs de x pour lesquelles on pourra calculer f(x) et g(x), donc [0;4]
Oui c'est bien cela mais ce qui me gène c'est que l'ensemble donné est l'ensemble de définition de x (0 
x 4) mais pas de f(x)
j'aimerais bien savoir ce que tu appelles ensemble de définition d'une fonction, si ce n'est l'ensemble des x pour lesquels on peut calculer une image par cette fonction 
Pour moi , mais je peux me tromper , l'ensemble de définition de f(x) est du type a < f(x) < b (toutes les valeurs que peut prendre f(x)) différent de l'ensemble de définition de x (toutes les valeurs que peut prendre x).
Bah si on prend la définition de "l'ensemble de définition du'une fonction" ca donne :
L'ensemble ou domaine de définition d'une fonction ƒ est l'ensemble de tous les réels x pour lesquels ƒ(x) existe ou est calculable
Donc on cherche bien les valeurs que x peux avoir.
Donc NI-IcO tu as juste l'ensemble de définition des 2 focntions est [0;4].
fm_31, ce que tu dis est l'ensemble image de f ... et ça n'est pas forcément un intervalle, voir par exemple la fonction inverse ....
pour les expressions algébriques pour y voir clair en math le mieux c'est de bien tout résumer ce dont on a besoin pour répondre à la question et de traduire en langue math ce que dis l'énonce.
Je t'aide pour f(x)
f(x) le volume de SABCD donc f(x) = VSABCD
Ce qu'on veux c'est donc exprimer le volume de SABCD en fonction de x.
SABCD c'est quoi ? 
une pyramide de sommet S et de hauteur SA et de base ABCD
Le volume d'une pyramide c'est quoi ? V = 1/3AbaseHauteur
Donc dans notre pyramide
VSABCD = 1/3 AABCDSA
Quel est l'aire de la base ? ABCD est un rectangle l'aire d'un rectangle est égale à la longeurla largeur donc ici AABCD = ABBC
On remplace tout ça dans notre formule et ça donne
VSABCD = 1/3 ABBCSA
Tu connais AB tu connais BC et on a posé au debut de l'énoncé de la question que SA = x
Tu peux donc exprimer VSABCD en fonction de x et du coup trouver f(x)
Je te laisse faire la fin des calculs.
Pour g(x) tu procède de la même facon.
Je récapitule:
1) (figure plus haut)
2) a) & b) D= [0;4]
a) f(x) = 1/3 * 30 * x
b) ES = AE - x
On peut utiliser Pythagore dans EFH
lafol >>> j'aimerais bien savoir ce que tu appelles ensemble de définition d'une fonction, si ce n'est l'ensemble des x pour lesquels on peut calculer une image par cette fonction
Oui mais comment connaitre cet ensemble tant qu'on n'a pas formulé la fonction ? Certes on peut conjecturer .
La question aurait été moins ambigue sous la forme par exemple : Donner le domaine de variation de x .
Vous vous embrouillez, l'ensemble de définition de f et de g , c'est [0;4] c'est a dire que x peut varier entre 0 cm et 4 cm..
c'est a dire que x peut varier entre 0 cm et 4 cm..
Pour f(x) ton calcul est juste, par contre tu peux encore le simplifié.
Pour g(x) oui SE = AE - x mais tu as besoin d'autre chose pour déterminé g(x).
Tu es d'accord que g(x) = VFESH
on sait que V = 1/3AbaseHauteur
A toi de trouver l'aire de la base, la hauteur tu l'a déjà trouvé.
Attention à la forme géométrique de ta base ce n'est pas la même que la précedante.
Pour être sur de ne rien oublié marque bien toute tes étapes comme j'ai fais pour f(x)
Oui mais comment connaitre cet ensemble tant qu'on n'a pas formulé la fonction ? Certes on peut conjecturer .
La question aurait été moins ambigue sous la forme par exemple : Donner le domaine de variation de x .
Il n'y a pas d'ambiguïté c'est juste que ce que tu appelle "domaine de variation de x" ca s'appelle en maths "ensemble de définition de la fonction". Et ici pas d'ambiguïté l'énoncé te donne clairement les valeurs possible de x.
Pour trouver l'aire de la base je doit connaitre la taille de tout les arretes. Donc j'utilise le theoreme de pytagode dans le triangle EFG:
HF² = FE² + EH²
HF² = 6² + 5²
HF² = 36 + 25
HF² = 61
HF = 
61 (valeur exacte)
HF 
7.8
En fait je pense que on a pas besoin de Pythagore:
Abase = (5*6)/2
Donc
g(x) = 1/3 * 15 * (5-x)
je me demande si fm_31 ne s'embrouille pas à cause de la nuance entre "ensemble de départ" et "ensemble de définition"
ici, il est clair que l'ensemble de départ est [0;4], mais il ne faut pas longtemps pour s'assurer qu'on pourra calculer les volumes des pyramides concernées pour tout x de [0,4], même sans avoir l'ombre d'une idée de comment le calculer, et que donc l'ensemble de définition aussi est [0,4]
ici, il est clair que l'ensemble de départ est [0;4], mais il ne faut pas longtemps pour s'assurer qu'on pourra calculer les volumes des pyramides concernées pour tout x de [0,4]
Comme le dis lafol, la hauteur est SE = 4-x, c'est ce que tu as écrit dans ton post précédant en plus .
Sinon l'aire de ta base est juste (et oui pas besoin de pythagore)
Je te conseille sur ta copie de bien marquer la forme littérale de tes formules et tes rélfétions car cela peut te couter des points.
As tu simplifié f(x) ? quel résultat as tu ?
Quel est ton résultat final pour g(x) ?
Si tu es sur de toi tu peux faire la suite de ton exercice.
Pour la question 3 il te suffit de traduire l'enoncé de la question sous forme mathématique, donc en gros tu va avoir une équation avec f(x), g(x) et 1 ou plusieurs signes mathématiques (+ - * / =). Cela te pose problème ?
C'est ca.
Donc si on résume
VSABCD = f(x) = 1/3 * 30 * x = 10*x
VSEFH = g(x) = 20-5x
Quelle équation toi tu résoudres pour la question 3 ?
Je pense que ça serait :
g(x) = f(x) [ ou l'inverse ça reviens au même]
20-5x = 10x
20-5x-10x = 0
-5x-10x = -20
-15x = -20
x = 20 / 15
C'est le même principe tu traduits la phrase en langage mathématique.
Trouver X pour que :
"volume de SABCD" f(x)
"est supérieur" >
"au tiers" 1/3
"du volume de SEFH" g(x)
Donc il faut résoudre f(x) > 1/3*g(x)
Tu as compris le résonnement ?
Bah c'est exactement la même chose que si tu avais f(x) = 1/3*g(x)
Tu resouds ça de la même façon c'est juste qu'a la fin tu n'auras pas x = nombre mais x > nombre
J'aimerais bien que tu m'envoie ton calcul détaillé s'il te plait.
Je ne trouve pas pareil (c'est possible que ce soit moi qui est faux aussi )
Sache que plus tu simplifie tôt une fraction plus tu te simplifie la vie.
Désolé du temps mais je sais pas, je crois que Iles Des Math a eu une maintenance..
voila mes calculs:
10x > 1/3 * 20 -5x
10x > 20/3 -5x
10x + 5x > 20/3
15x > 20/3
x > 20/3/15
Voila c'est comme çà que j'ai fait.
Alors attention il te manques des parenthèses très importante
Là à droite tu dois avoir 1/3*g(x) ce qui revient à marquer 1/3*(20-5x) et surtout pas 1/3*20-5x
Quand tu développe tu multiplies 1/3 par 20 ET par -5x tu as oublié cette dernière partie. Il faut refaire le calcul.
Une petite aide pour éviter d'avoir un truc du type
Rappelle toi de la règle " diviser, c'est multiplier par l'inverse"
Dans mon exemple A/B est diviser par C donc d'après cette règle A/B est multiplié par 1/C (= l'inverse de C) donc je peux l'écrire sous cette forme
Et là normalement c'est une forme que tu sais simplifier sans problème
Donc
10x > 1/3 * (20-5x)
10x > 20/3 - 5x/3
10x + 5x/3 > 20/3
10x*3/3 + 5x/3 > 20/3
(30x + 5x) /3 > 20/3
35x/3>20/3
En fait je crois que je me suis trompé quelques part..
Annuler
connectez vous