Bonjour Sidix et bienvenue,
mais as-tu lu ceci ? Sujet ancien- ne plus donner ce lien-merci

je te demande donc de reprendre point par point, suite à ma réponse
tu mettras ton énoncé, la figure s'il y en a une, ainsi que tes pistes de refléxion
ensuite, tu pourras avoir de l'aide
pour la figure :

extrait de la FAQ du forum :

Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?

Vous souhaitez ajouter une image ou un pdf à votre message . Veuillez obligatoirement respecter ces règles :

Énoncé d'exercice ou de problème :

Pour les énoncés courts (moins de 5 lignes sur une feuille A4) :
La recopie est obligatoire.
L'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !

Pour les énoncés longs  :
Les 5 premières lignes sont à recopier pour aider l'archivage des sujets sur le site.
Cela fait, l'énoncé dans sa totalité, pourra alors être joint en image (choisir Img) ou en pdf (choisir Pdf ) mais dans le respect des droits d'auteurs en vigueur. Pour les pdf, merci d'en préciser la source.

Recherches (même non abouties) de l'exercice :
Elles doivent être obligatoirement recopiées, et ce, dès la demande d'aide.
l'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !
Les formats autorisés sont exclusivement les suivants : gif, jpg, jpeg, et png. La taille d'un fichier est limitée à 2 MO maximum pour une image et à 500 ko pour un pdf.

Le non respect de ces règles entraînera la suppression du contenu de votre sujet (même si des réponses ont été apportées) et éventuellement la suspension de votre compte !

Seule exception : Dans le forum détente, des réponses longues et élaborées , contenant plusieurs images explicatives, pourront être postées sous forme d'image ou de pdf. Les énoncés, quant à eux, devront toujours être rédigés sur le site (indispensable pour le référencement).

Bonjour j'ai compris la question 1 mais je sais pas comment la répondre, si quelqu'un peut me la faire, c'est mon professeure qui me la donner en guise d'apprentissage
pour le controle a la rentrée.

** image supprimée **
tu comprends le mot "recopier" ??

*** message déplacé ***

et maintenant un multipost
on va te forcer à lire vraiment les règles.

extrait de la FAQ du forum :

Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?

Vous souhaitez ajouter une image ou un pdf à votre message . Veuillez obligatoirement respecter ces règles :

Énoncé d'exercice ou de problème :

Pour les énoncés courts (moins de 5 lignes sur une feuille A4) :
La recopie est obligatoire.
L'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !

Pour les énoncés longs  :
Les 5 premières lignes sont à recopier pour aider l'archivage des sujets sur le site.
Cela fait, l'énoncé dans sa totalité, pourra alors être joint en image (choisir Img) ou en pdf (choisir Pdf ) mais dans le respect des droits d'auteurs en vigueur. Pour les pdf, merci d'en préciser la source.

Recherches (même non abouties) de l'exercice :
Elles doivent être obligatoirement recopiées, et ce, dès la demande d'aide.
l'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !
Les formats autorisés sont exclusivement les suivants : gif, jpg, jpeg, et png. La taille d'un fichier est limitée à 2 MO maximum pour une image et à 500 ko pour un pdf.

Le non respect de ces règles entraînera la suppression du contenu de votre sujet (même si des réponses ont été apportées) et éventuellement la suspension de votre compte !

Seule exception : Dans le forum détente, des réponses longues et élaborées , contenant plusieurs images explicatives, pourront être postées sous forme d'image ou de pdf. Les énoncés, quant à eux, devront toujours être rédigés sur le site (indispensable pour le référencement).

extrait de la FAQ du forum :

Q03 - Pourquoi ne faut-il pas faire du ''multi-post'' ?

Pour de nombreuses raisons.

Pour mémoire, le multi-post consiste à reposer une même question dans un sujet différent , ou à poser des questions successives d'un même problème dans des sujets différents.

De même, une demande identique sur plusieurs sites sera considérée comme un multipost et la discussion pourra être fermée par un modérateur.

Etant donné tous les désagréments créés par le multi-post, le non-respect de cette règle entraînera votre exclusion temporaire ou définitive du forum !

Voici maintenant quelques raisons qui font que nous combattons avec autant d'ardeur le multi-post (et ses adeptes ) :

• La perte de temps pour les modérateurs qui consacrent leur temps bénévolement pour garantir la qualité des sujets et des échanges sur le forum.
• Le respect du travail des correcteurs qui consacrent leur temps bénévolement pour aider ceux qui sollicitent de l'aide.
• La lisibilité du forum de manière à ce qu'un sujet ayant déjà reçu de l'aide soit facilement identifié et qu'un sujet n'en ayant pas encore reçu puisse à son tour en recevoir.

Rappelez-vous une nouvelle fois la règle d'or du forum :
1 sujet créé = 1 problème

extrait de la FAQ du forum :

Q30 - J'ai été averti ou banni, pourquoi, et que faire ?

J'ai été averti ou banni parce que je n'ai pas respecté les règles du forum, qui étaient à lire avant de poster. et donc acceptées tacitement lors de l'inscription.

Ou bien j'ai un triangle rouge devant mon pseudo et je suis averti. Je peux réagir dès que je le désire, en m'engageant à respecter le règlement (une phrase à recopier), et je peux lever mon avertissement moi-même. Pour cela, je tente de répondre à mon message, et la procédure apparaît.
Un conseil cependant : vraiment lire le message "A lire avant de poster" et ne pas récidiver...Vous seriez alors banni.

Si je suis averti pour ne pas avoir respecté la manière de poster expliquée en Q05 , je relis Q05 , puis je lève mon avertissement et je reposte mon énoncé correctement cette fois, dans le même sujet, et ainsi j'obtiendrai de l'aide rapidement très certainement.

Ou bien ma figurine est masquée, j'ai été banni pour un certain temps, et je dois en attendre la fin.

Bonjour j'ai compris la question 1 mais je sais pas comment la répondre, si quelqu'un peut me la faire, c'est mon professeure qui me la donner en guise d'apprentissage
pour le controle a la rentrée
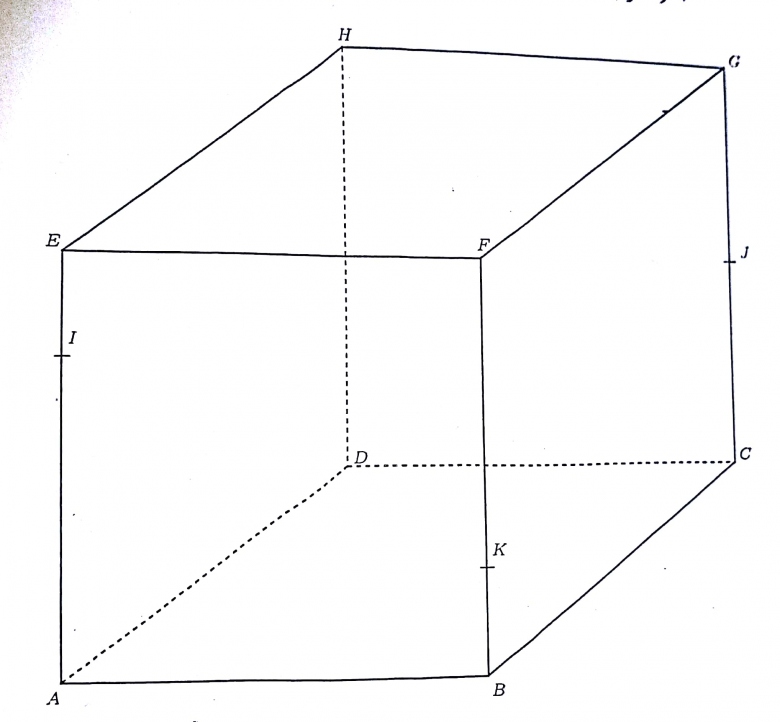
L'énoncé : Soit ABCDEFGH un cube.

I J et K les points définis par
AI(vecteur)=3/4AE CJ= 1/2CG BK = 1/4 BF
La figure:


Question 1: Démontre que IHJK est un parallélogramme
Questions 2 Les Droites (IK) et (BC) sont elles secantes ?
Et aussi la question 2  que j'ai pas trop compris
Merci et désolé pour le non respect des règles j'étais préssé.

** image supprimée **
(recadrée sur la seule figure,
le faire à la prise de vue aurait permis de la faire plus lisible !!)

("me la faire" surement pas !!
on peut t'aider à la faire, pas la faire à ta place)

Question 1 :
déja refaire ta propre figure (plus lisible !) avec les points I,J K dessus

on peut la résoudre par les vecteurs en prouvant (avec des applications de Chasles) que les vecteurs IH et KJ sont égaux.

ou dans un repère, par exemple; (A; AB; AD; AE)

créer un repère, celui là ou un autre éventuellement plus judicieux, même si on ne s'en sert pas vraiment , peut aider à trouver comment décomposer par Chasles : selon les vecteurs du repère.

la question 2 : après la question 1 ...

(PS : je devrais quitter dans l'après midi)

Résoudre par Chasles c'est à dire, j'ai penser a dire que IH=k IJ en gros ils sont colinéaires
IH est un multiple de IH et inversement, j'ai faux?

Du coup j'ai fais ça mais je sais pas comment faire apres  : IA + AB = GH + GJ

Désolé je me suis trompé : IA + AB + BK = HD + DC + CJ mais je suis pas quoi faire apres pour prouver que c'est un parallélogramme

La figure en question.

mathafou tu es disponible ? Si oui, merci

le démarrage du reconfinement m'a rendu indisponible hier.

dans un parallélogramme c'est les vecteurs sur les cotés opposés qui doivent être égaux (et pas seulement colinéaires) :
côtés parallèles, de même sens et de même longueur

les côtés opposés ici seront par exemple IH et KJ
donc on veut montrer que en vecteurs IH = KJ
sont égaux

pour cela on va décomposer chacun d'eux selon des arêtes du cube :
IH = IE + EH
du même genre pour KJ
par exemple : KJ = KB + BC + CJ

puis tenir compte des définitions de E, K et J pour obtenir IE en fonction de AE (ne plus avoir que des arêtes du cube) etc

et tenir compte que les arêtes du cube sont deux à deux égales.

Merci pour la réponse.

IH = IE + EH
  =1/4AE + FG
=1/4BF + FG
KJ = KB + BC + CJ
=1/4FB+ FG + 1/2CG
=-1/4BF+FG+2/4CG
=-1/4AE+FG+2/4CG
=-1/4AE+FG+2/4AE car CBFG et BFEA carré
=1/4AE + FG
IH = KJ donc IHJK parallélogramme
C'est ça ? Si c'est ça, j'écris ça dans ma copie pour la première question ?
Merci encore pour la réponse et pour votre aide

IH =1/4AE + BF du coup .

+ FG* ( onj peut modifier les réponses  sur ce site?)

impec.

C'est grâce à vous ! je vous remercie !

on ne peut pas modifier les réponses, on ajoute une réponse corrective
(vu que AE = BF c'est du pareil au même, mais le dire explicitement était effectivement à ajouter)

D'accord, concerant la question 2, je vois qu'elle est sécante mais je ne sais pas comment la justifier.

"je vois" en perspective peut être une parfaite illusion d'optique !!

pour démontrer ou infirmer, il faut considérer tous les plans dans lesquels se trouvent ces droites
(si elles se coupent elle devraient être dans un même plan)

Je n'ai pas bien compris, vous avez un exemple ?

IK inclus dans ABFE
BC inclus dans BCFG
Les deux plans se coupent, donc ils sont sécants ? Dans un meme plan ? J'ai pas bien compris

les deux plans se coupent , OK
selon quelle droite d'intersection ?

l'intersection de (IK) et de (BC) étant un point appartenant à ces deux droites , donc à ces deux plans doit donc être sur cette droite d'intersection là

en d'autres termes, les intersections de (IK) avec la droite commune et de (BC) avec la droite commune devraient être confondues pour que ce soit l'intersection de (IK) et de (BC)

conclusion... ?

IK inclus dans ABFE
BC inclus dans BCFG
Les deux plans se coupent en (BF)
(EAB)∩(BCG) = (BF) Donc les droites sont sécantes?

IK inclus dans ABFE
BC inclus dans BCFG
Les deux plans se coupent en (BF)
(EAB)∩(BCG) = (BF)

oui

Donc les droites sont sécantes?
n'importe quoi !

on te demande si elles sont sécantes
et la réponse sera oui ou non
avec justification
(et c'est évident ...)

Justement je sais pas comment on démontre, on doit utiliser quel outil? (car je n'ai pas encore fait ce type d'exo en classe)

je t'ai tout dit , il n'y a rien de plus qu'à comprendre ce que j'ai dit
les seuls et uniques "outils" là dedans c'est l'appartenance ou pas de points à des droites qui sont dans des plans et rien d'autre que savoir raisonner sainement de façon la plus générale.

Je dis : l'intersection des droite (IK) et (BF) n'ont pas le même point d'intersection sur la droite (BF) donc elles sont sécantes ?

je ne comprends pas que tu ne voies pas immédiatement (fais le avec tes mains vraiment et le coup de la boite d'allumette)
que (IK) et (BC) ne sont PAS sécantes du tout


la droite (IK) passe largement devant la droite (BC), elles ne risquent pas se rencontrer !

formellement :
comme je le disais, si elle se rencontraient ce serait forcément en un point de la droite (BF), intersection du plan (ABF) contenant (IK) et (BCF) contenant (BC)
or (IK) coupe (BF) en K, vu dans le plan (ABF), et (BC) coupe (BF) en B, vu dans le plan (BCF)
K et B sont distincts
donc les droites (IK) et (BC) ne se coupent pas.

Le point d'intersection apparent (cercle rouge) sur la figure n'en est pas un en vrai : c'est une illusion d'optique due à la perspective.

autre preuve en considérant les plans (ABC) et (ABF) :
dans (ABF) : (IK) coupe (AB) en S, point d'intersection de (IK) avec le plan (ABC)
ce point n'appartenant pas à la droite (BC) de ce plan (ABC), les droites (IK) et (BC) ne se coupent pas.


_{(en bleu dans ma figure une preuve sans vecteurs de "IHJK est un parallélogramme"
en prouvant que EHJM et IEMK en sont, donc que [IK] et [HJ] sont parallèles et égaux)}

Merci pour ces résponses ! désolé je n'ai pas eu la notification pour répondre.

les notifications fonctionnent de façon un peu aléatoire par moments
le mieux est d'aller voir par soi même où ça en est (bouton "mes messages")