Inscription / Connexion Nouveau Sujet
Exercice dans un cube
Bonjour !
Voilà l'exercice :
ABCDEFGH est un cube. I  [AE], J
[AE], J  [BF] et K
[BF] et K  [BCGF]
[BCGF]
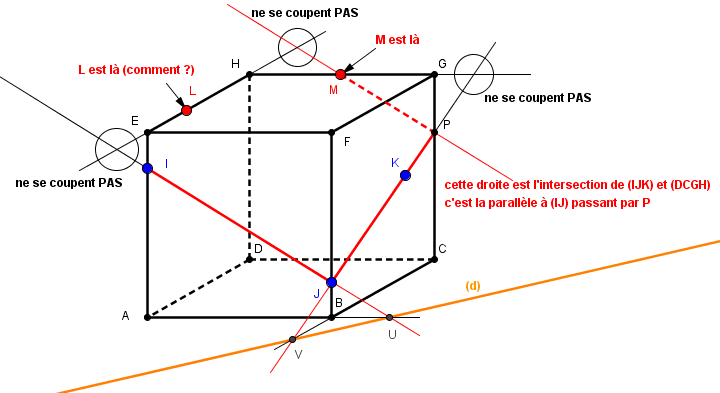
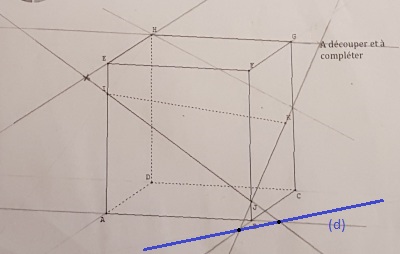
1) Construire la droite (d) intersection des plans (IJK) et (ABC). Expliquer la construction.
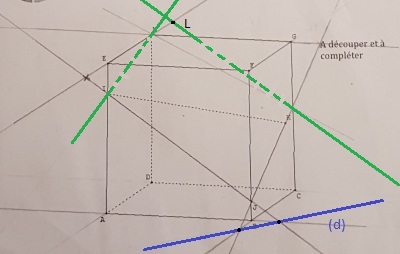
2) Construire la section du cube par le plan (IJK). On notera notamment L l'intersection de la droite (EH) du plan (IJK) et M l'intersection de la droite (HG) du plan (IJK).
3) Justifier que les droites (d) et (LM) sont parallèles.
Je crois que j'ai trouvé la droite (d) ainsi que la section du cube par le plan (IJK) mais je ne trouve pas (LM) alors mes constructions sont peut-être fausses.
Merci d'avance pour votre aide !
2) Pour construire les points L et M, tu pourrais chercher l'intersection du plan (IJK) et des plans (ADHE) et (DCGH), respectivement.
Bonjour,
les données ne sont pas suffisamment précisées pour permettre de faire une figure sans ambiguïté :
la forme même de la figure, voire l'existence des point cités, dépend fortement de la position précise des points I, J et K sur leur support respectifs.
par exemple :
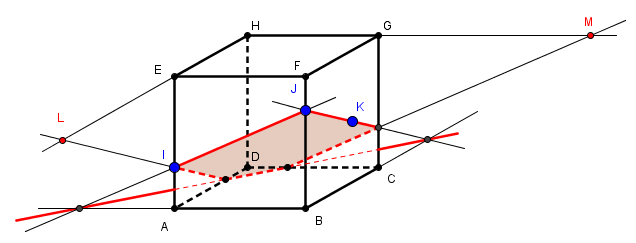
parmi de nombreuses autres figures et constructions possibles
Bon la figure est venue entre temps...
(le principe est le même
ta section est fausse car H ne fait pas partie du plan (IJK) et donc pas de la section non plus)
Encore désolé !
Pourtant H se trouve sur EHDA et comme I  [AE], on pourrait faire une section avec (IH) ?
[AE], on pourrait faire une section avec (IH) ?
Une section avec quoi ?
Pour placer le point L, as-tu déterminé l'intersection des plans (IJK) et (ADHE), dont un point est déjà connu ?
Hmm non c'était une idée mais ça ne marche pas.
Je crois avoir trouvé les points L et M mais pour la droite (d)...
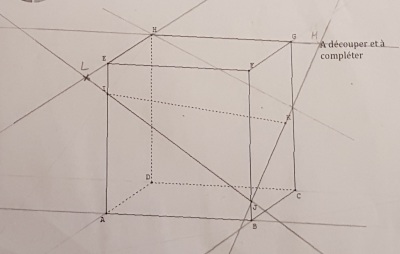
La droite (d), je croyais que tu l'avais déterminée au vu de ta première figure.
Mais je ne distingue pas bien comment tu as fait.
Pour une figure plus claire, je te conseille de remonter un peu le point J sur l'arête BF.
Oui mais je crois que je m'étais trompée pour la droite (d) car j'avais prolongé (IH) et (AD) pour obtenir un point (que j'avais appelé A') et l'a rejoint avec B' (prolongement de (BC)). Or le prolongement (IJ) ne rencontrera jamais cette droite (d) que j'avais tracé car ils ne sont pas du même plan.
Pour le point J, en fait je ne peux pas le remonter car le professeur nous a donné cette figure qu'il avait déjà faite et sur laquelle nous devons faire les sections.
Un premier point de la droite (d) est le point où la droite (IJ) perce le plan (ABCD). Peux-tu construire ce point ?
pour les points L et M c'est totalement faux car les droites (IJ) et (EH) ne sont même pas dans un même plan
et donc ne se coupent même pas en le point que tu as imaginé être L etc ...
et pareil pour M
pour ces points L et M il faut utiliser la propriété :
"les intersections d'un plan donné avec deux plans parallèles sont des droites parallèles"
mais n'anticipons pas.
il faut déja faire la question 1 ...
et bien entendu avant de faire la question 2
vu que ton premier dessin semblait bien avoir fait le contraire :
une question 2 fausse, puis dont tu as tiré une droite (d) un peu beaucoup fantaisiste, même si il y en avait un point de bon !!
(dont le nom est totalement illisible)
pour la droite (d) oui,
pour tes points d'intersection farfelus avec (EH) et (HG) surement pas
(déja dit et c'est toujours vrai)
la clé est ici, aussi bien pour trouver les points L et M que pour la question 3 ce que j'ai déjà dit :
"les intersections d'un plan donné avec deux plans parallèles sont des droites parallèles"
les plans (ADHE) et (BCGF) sont parallèles, les intersections de (IJK) avec ces deux plans sont donc deux droites parallèles
on connait l'intersection avec (BCGF)
donc on en déduit l'intersection avec (ADHE) et donc le point L
pareil pour M
pas terrible et tu continues à imaginer des points de concours de droites qui ne se coupent pas dans l'espace parce qu'elles sont dans des plans complètement différents
par exemple ta droite parallèle à (IJ) (qui devrait) se trouve dans le plan (DCGH) c'est l'intersection du plan (DCGH) et du plan (IJK), c'ets pour ça qeu c'est la parallèle à (IJ)
mais ce plan là (DCGH) coupe "évidemment" la droite (EH) en H
et donc toute droite de ce plan (DCGH) qui couperait (EH) ne pourrait le faire que en ce point H ou bien pas du tout.
ton point L n'existe pas.
la droite (EH) passe en dessous de la parallèle à (IJ)
de même (IJ) passe en dessous de (EH) et ne la coupe pas
et (JK) passe en dessous de (GH) et ne la coupe pas
de plus on va lourdement insister sur le fait déja dit et redit que H n'appartient pas du tout au plan (IJK) et donc n'appartient pas du tout à la section du cube par ce plan
(sauf coup de bol faramineux sur les positions précises de I, J, K qu'elles n'ont pas dans cette figure)