Inscription / Connexion Nouveau Sujet
Exercice de fonction avec ln
Bonjour, j'ai un exercice à faire et je n'ai vraiment rien compris. Pourriez vous m'aider et surtout m'expliquer. Merci.
Partie A :
(Cf) est la courbe représentative d'une fonction f dans un repère orthonormal. La tangente T à (Cf) au point A de coordonnées (1;1/2) a pour coefficient directeur -3 (f'(1)=-3)
1) Donner f(1) et f ' (1)
f est définie sur l'intervalle ]0;+[ par f(x) = ax2+bx-4lnx où a et b sont deux réels.
2) Calculer et exprimer f ' (x) en fonction de a et b.
3) Justifier que a et b sont solution du système a+b = 1/2
2a+b = 1
et déterminer a et b.
Partie B :
On admet que f définie sur l'intervalle ]0;+[ par f(x)= 1/2 x2 - 4 lnx
1) Calculer lim f(x) en x
0. Interpréter graphiquement ce résultat.
2) Vérifier que f(x) = x (1/2 X - 4 lnx/ x) et en déduire lim f(x) pour x+
3) Calculer f ' (x) pour tout x de ]0;+[
4) Etudier le signe de (x2 - 4) sur 
. En déduire le signe de f ' (x) sur ]0;+[ et donner les variations de la fonction f.
5) Compléter le tableau de valeurs donné en annexe A a 10-1.
6) Dans un repèe orthonormal d'unité graphique 2cm, tracer en annexe A la tangente à (Cf) au point d'abscisse 2, la tangente (T) et la courbe (Cf).
pour le 1) on te donne la réponse dans l'énoncé
pour le 2) dérive la formule puis ecris f(1) et f'(1)
Bonjour
qu'est-ce qui vous pose problème dans la partie A
f(1)=
vous l'avez donné
que vaut la dérivée de dérivée de fonctions usuelles
si que valent
et
?
en utilisant les renseignements de la première question vous avez le système qu'il suffit maintenant de résoudre pour avoir et
Bonjour, alors j'ai trouvé pour la partie A mais je ne sais pas si c'est bon.
F(1)=1/2 car d après les coordonnées de T, y=1/2.
f ' (1)=-3 comme dit dans l énoncé car c'est le coefficient directeur.
2) f(x)=a x 2x + b x 1 - 4 x 1/x
f ' (x ) = a 2x + b -4/x
3) pour vérifier que a et b sont solutions du systèmeme il faut retrouver la même chose en haut et en bas.
Donc pour en bas je divisé par deux à gauche donc aussi à droite et ça me donne
a + b = 1/2
a + b = 1/2.
Je ne sais pas si c est la bonne manière de l expliquer.
Comment trouver a et b du coup ? En utilisant la formule ?
Non je me suis trompé je ne me rappelais plus des systèmes.en fait je dois soustraire à la deuxième équations les membres de la première.
Cela me donne a = 0,5.
Ensuite je remplace a dans une des deux équations. Je choisis la deuxième soit je trouve b =0
Donc f(x) = 0,5x
?
attention à la casse est différent de
et si vous avez vu les primitives le sens est différent
on est amené à résoudre
en soustrayant on obtient bien et en remplaçant dans une équation
vous avez oublié une partie de la fonction
ce qui est bien la fonction définie dans la partie B
Oui je me suis trompée ça a écrit une majuscule car je suis en début de phrase. C'est bien petit f.
Merci.
Jai commencé mais j'ai un peu de mal.
Pour la limite Jai pris les limites de chaque membres séparément et cela me donne pour la limite entière et cela me donne + infini quand x tend vers 0 et je pense que cela est vont car Jai vérifie sur la courbe de la calculatrice. Cela signifie donc que cela ka droite x=0 est asymptote verticale à Cf.
Pour le 2) Jai distribué la formule donnée et je retrouve celle de départ.
Pour en déduire la limite Jai un peu de mal . Jai aussi pris la limite de chaque membre comme tout à l'heure et j arrive à un limite totale quand x tend vers + infini de 0. Je pense que ça doit être bon car Jai vérifie sur graph.
limite de chaque membre ?
il n'y a pas de problème on a l'axe des ordonnées est bien asymptote à la courbe
en
il aurait suffi de dire on met en facteur
on sait que
comment avez-vous un tel graphique ?
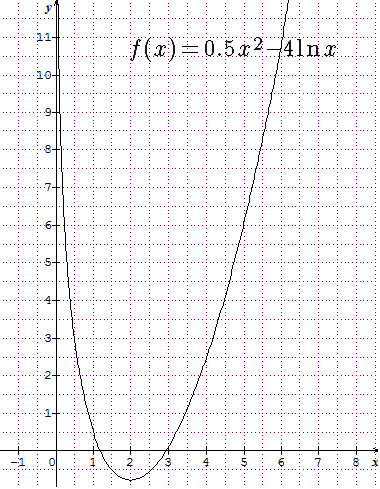
pour le reste avez-vous des problèmes ?
pour la dérivée faites remarquer que c'est le résultat trouvé en partie A et il vous suffit alors de remplacer a par sa valeur
ce n'est pas la peine de se fatiguer à tout recommencer
dans la partie A vous aviez une fonction définie par et
on sait que et
donc
et comme dans la partie B c'est cette fonction donc on a déjà
mais si vous voulez dériver à nouveau personne ne vous en empêche
Alors pour la question 4 si Jai bien compris il faut favoriser x - 4/x et ça nous donne (x2-4) ?
Après je fais un tableau de signes et J'en déduis les variations de f
question Étudier le signe de sur
. En déduire le signe de f ' (x) sur ]0;+[ et donner les variations de la fonction f.
donc il faut bien commencer par factoriser
Donc je fais mon tableau à partir de f'(x) = x^2-4. Donc c'est toujours positif car un carré l est toujours mais ça va pas parce que la variation n'est pas que croissante non ?
vous aviez parler de factoriser
dans ce que vous dites je ne vois pas de factorisation à moins que vous ne répondiez pas à la question :"étudier le signe sur " mais que vous teniez compte
de l'ensemble de définition
Ça y est Jai tout terminé.
Je vous remercie beaucoup car vous m avez bien aidé et jai mieux compris.
Bonsoir.
Annuler
connectez vous