Inscription / Connexion Nouveau Sujet
Exercice de géométrie dans un cube
Bonjour, j'ai un exercice à rendre voici l'énoncé :
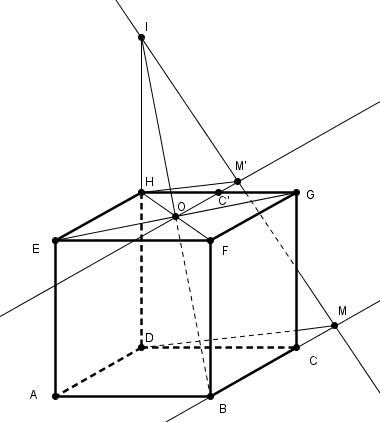
Soit un cube ABCDEFGH. On désigne par I le symétrique de D par rapport à H, O est le centre de la face EFGH et M un point de la droite (BC). La droite (IM) coupe le plan (EFG) en M'.
1) Où se situe M' si M=B ?
Où se situe M' si M=C? (On appellera ce point C')
Je trouve que M'=O et que C'=1/2HG
2) Soit M différent de B. Démontrer que la droite (M'O) est parallèle à la droite (BC).
Je bloque pour cette question.
3) Démontrer que M' est le milieu de [IM].
J'ai réussi cette question.
4) En déduire l'ensemble des points M' lorsque M décrit le segment [BC].
J'ai trouvé que que le point M' décrivait le segment [OC'].
Merci d'avance pour votre aide
Bonjour,,
mauvaise compréhension du français ? faute de frappe ? erreur de raisonnement ? va savoir ...
Où se situe M' si M=C? (On appellera ce point C')
veut dire que lorsque M est en C alors le point M' lui même on l'appelle C'
la correspondance M  M' est une application qui à tout point M (de (BC)) fait correspondre un point M'
M' est une application qui à tout point M (de (BC)) fait correspondre un point M'
appeler C' l'image de C par cette "transformation" est parfaitement naturel
en tout cas :
dire que dans ce cas M' est en O et que le même point simplement renommé en C' est aussi en même temps ailleurs est une erreur grossière ...
(sans même regarder où il est pour ma part, rien qu'en lisant ce qui est écrit c'est aberrant)
reprenons donc à zéro.
ton affirmation M' = O est simplement fausse
et C' = 1/2HG si on comprend bien ce "raccourci oratoire" en "C' est le milieu de GH" est juste
(un point n'est pas la moitié d'une longueur !! "GH" veut dire la mesure de [GH] 1/2GH veut dire la moitié de cette mesure)
question 2
considérer le plan (IBM), ce plan est fixe et est en fait le plan (IBC),
théorème : si un plan, (IBM), coupe deux plans parallèles, (ABC) et (EFG), alors les intersections sont parallèles
le reste est OK.
Bonjour,
ça dépend ce que tu connais comme moyens de démonstration.
le plus simple est d'utiliser l'homothétie de centre I qui transforme D en H (de rapport 1/2) et donc aussi M en M' (parce que IM/IM' = ID/IH c'est Thalès entre IHM' et IDM ou encore la droite des milieux)
tu as déjà démontré que B se transformait en O et que M se transformait en M'.
on sait que par homothétie, une droite se transforme en une droite parallèle.
donc la transformée de BM est une droite parallèle et comme elle passe par O et M', c'est OM'.
3) est alors evident, 4) aussi

en relisant c'est moi qui avais mal lu
Où se situe M' si M=B ?
Où se situe M' si M=C ?
deux questions
et donc deux réponses (justes) :
M'=O 1ère réponse (à la première question ! que j'avais zappée) juste donc
et que C'=1/2HG 2ème réponse (à la deuxième question) juste donc aussi comme déja dit (mais pas très bien exprimée)


