Inscription / Connexion Nouveau Sujet
exercice de maths triangle isocele et reperage de plan
Voici l'intitule de l'exercice :
Soit un triangle abc isocele en a et i le milieu de [bc] . Ça c'est ok j'ai compris et je l'ai fait.
1.determiner un repere du plan ( qu.es-ce que c'est ? ) dans lequel A et B ont pour coordonnees respectives (0;1) (1;0). Alors dois-je faire un repere orthogonal et y inserer le triangle abc isocele ?
2. Determiner un repere orthogonal dans lequel A et C ont pour coordonnees respectives (0;1) (1;0). Je n'ai pas reussi le precedent, celui-là non plus.
B. Dans ce repere, quelles sont les coordonnees des points I et B ? Je ne sais pas comment ces points sont apparus.
Le probleme de cet exercice est qu'il est trop vague et nous venons a peine ( aujourd'hui) d'aborder le reperzge dans un plan.
Alors j'aimerai vriment qu'on m'explique comment proceder pour les questions 1,2 et B, et a la limite une correction, car j'ai besoin de me mettre vraiment a travailler en maths, car je viens de rentrer en seconde.
Merci d'avance pour votre aide.
Bonjour 
Alors dois-je faire un repere orthogonal et y inserer le triangle abc isocele ?
Non c'est plutôt l'inverse, tracer le triangle et ensuite trouver le repère qui correspond pour les coordonnées des points donnés. (attention on ne te dit pas que le repère doit absolument être orthogonal ou orthonormé...)
Oui mais je n'arrive pas apres construction du triangle isocele a trouver un repere qui puisse avoir comme coordonnee (0;1) pour A,car ça signifierait que le repere doive couper le triangle isocele en deux ?
Oui mais quelle est l'origine, A ?
Sincerement, je m'enmêle un peu les pinceaux, je n'ai jamais ete autant perdu.
Oui, ça je l'ai compris mais ce que je n'arrive pas a faire c'est placer les coordonnees.car j'ai l'impression pour A par exemple qu'il ne peut pas avoir ET 0 sur l'axe des abscisses ET 1 sur l'axe des ordonnees.
Ah, je pense avoir compris, mais faire les vecteurs de cb et de ca etait-il necessaire ?
Pour ce qui est de la deuxieme question, suffit-il de constuire un repere orthogonal dans lequel A aurait pour coordonnee ( 0;1) et C (1;0) ?
Et pour la derniere question où trouvent-ont les points i et b ?
Bonsoir
comme tu le dis "il est trop vague"
et le pire on te fait le truc à l'envers, c'est maintenant une fois que tu as tracé ce triangle arbitraire sur ta feuille entièrement blanche sans même un quadrillage pour te rassurer, on te demande de plaquer la dessus un repère de ton invention "de sorte que" ...
eh oui, il faut s'y faire et prendre des initiatives et ma figure n'a aucune raison d'être la même que la tienne ni que celle de ton voisin de classe : chacun a son propre triangle bien à lui, et son propre repère bien à lui.
des repères pour la question A il y en a des infinités, même une fois qu'on s'est fixé le triangle ABC.
yogodo t'en a donné un, je t'en donne un autre :
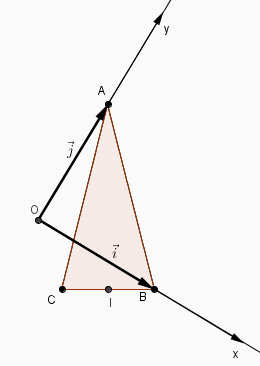
Pour la question 2 par contre le repère n'est pas n'importe quoi il est orthogonal
donc là on a un peu restreint les choix possibles
puisque A est sur l'axe Oy et C sur l'axe Ox, et que l'angle des axes est de 90° c'est à dire l'angle AOC = 90°, le point O origine du repère n'est pas n'importe où dans le plan comme pour la question 1.
il reste que ce repère n'étant que orthogonal (et pas orthonormé) il en existe encore un bon paquet !
et tu en choisis un. (au pire si tu manques d'imagination tu peux t'inspirer de ma figure, c'est pas les bons sommets mais c'est le même principe : mon repère à moi il est même orthonormé !)
quant aux points B et I ils sont là depuis le début puisque tu es parti au départ de
Soit un triangle ABC isocele en A et I le milieu de [BC]
le problème est que avec tous ces choix là libres à volonté eh bien les coordonnées de B c'est n'importe quoi.
si tu fixes le repère que tu as choisi, tu peux déformer ton triangle en gardant A et C fixes aux coordonnées (0;1) et (1; 0) et obtenir autant de points B et I qu'on veut.
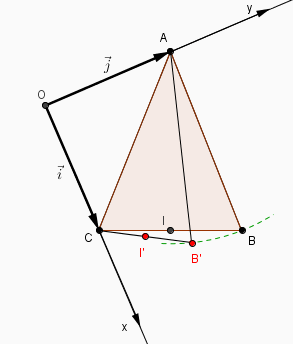
donc la question B (3 sans doute avec une tache sur le 3 qui en fait un B) est inepte.
le seul "truc" c'est que celui qui a posé le problème n'a pas vu ces infinités de repères possibles et à cru naïvement que le seul était avec l'origine en I !!
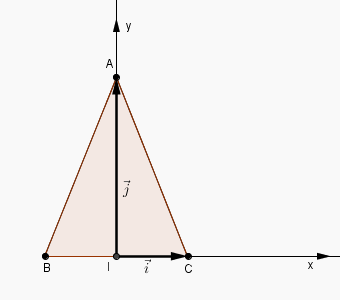
et du coup c'est toi qui es dans la mouise avec cet énoncé foireux.
tu n'as plus qu'à tenter d'expliquer ça au prof...
ou "par hasard" de deviner que c'était ce repère là qu'il attendait...
ce qui permet facilement de répondre à la question 3
Une réponse fausse mais une réponse "attendue"
Vous m'avez vraiment bluffé par votre pedagogie, ça me donne espoir de déchirer le plafond dans cette matière.
Pour en revenir au sujt pour tracer un repere de plan, on a besoin de deux droites ayant pour point de concours l'origine du repere (ici o ) et qui passent pas deux cotes de la figure ( que ça soit un triangle, un carre, ect ? ) car je ne savais même pas ce qu'etait un repere de plan
( et ne le sait d'ailleurs peut-etre roujours pas).
Pour B pourquoi avez-vous tracé b' c' ?
Donc pour la question les coordonnees de I et B seraient-ils respectivement (0;-1) ?
Merci beaucoup pour cette aide tres utile.
Pour tracer un repère du plan tel que dans ce repère les points donnés A et C par exemple aient pour coordonnées A(0; 1) et C(1; 0) on choisit une origine O n'importe où dans le plan et les vecteurs unitaires du repère :
en abscisse
en ordonnées
Alors par définition les coordonnées de C, extrémité du vecteur seront (1; 0)
et les coordonnées de A, extrémité de seront (0; 1)
Si on veut que ce repère soit orthogonal il suffit de choisir O pour que l'angle AOC soit un angle droit et donc il suffit de choisir O n'importe où sur le cercle de diamètre AC
Enfin si on veut que ce repère soit orthonormé il faut que l'angle en O soit droit et que OA = OC, donc les points du cercle précédent sur la médiatrice de AC
Donc dans la question 1 on peut choisir O absolument n'importe où comme dit ci dessus
Dans la question 2 on peut choisir O absolument n'importe où sur le cercle de diamètre AC.
Mais alors sur ma figure (2) précédente si on était parti de AB'C au lieu de ABC comme triangle de départ on aurait pu choisir le même repère, et donc les coordonnées de B sont indéterminées : elle valent n'importe quoi et il est impossible de répondre à la question 3 qui n'a alors aucun sens
Il reste que celui qui a posé le problème avait dans l'esprit (mais il ne l'a pas dit et il n'a rien donné dans l'énoncé qui permettrait de le déterminer) non pas "n'importe quel" repère mais les repères que lui pensait être la solution que lui voulait.
Et pour la question 1 au lieu de choisir n'importe quel point comme origine on choisit (arbitrairement) le seul point qu'on connait en plus de A et B dans l'énoncé : à savoir le point C comme origine et cela donne la figure de yogodo, avec comme origine O = C et comme vecteurs unitaires le point B aura donc bien comme coordonnées (1; 0)
et le vecteur unitaire et le point A aura bien comme coordonnées (0; 1) par définition des coordonnées
On aurait pu aussi bien choisir un autre point connu de la figure : I, mais cela aurait anticipé sur la question 2 !! donc on choisit C.
Pour la question 2, on devra choisir pour que la question 3 ait un sens
l'origine au point O = I (ma dernière figure), avec ses vecteurs unitaires
C'est la réponse "attendue" même si encore une fois rien dans l'énoncé, à part la simple existence de la question 3, ne permet de le "deviner".
Alors dans la question 3 on obtient les coordonnées de B et I de façon très simple :
I est bien entendu l'origine des coordonnées, on a choisi le repère d'origine I, ses coordonnées sont donc par définition (0; 0)
Quant à B on a en vecteurs et donc les coordonnées de B sont opposées à celles de C (I = O = origine !!)
soit B = (0; -1)
Voila un "corrigé" possible ...
(qui corrige à la fois l'énoncé foireux et le problème)
je ne savais même pas ce qu'etait un repere de plan
( et ne le sait d'ailleurs peut-etre roujours pas)
un repère du plan c'est le choix d'une origine O et de deux vecteurs dit "unitaires"
- la direction des axes : axe des abscisses Ox par
- les unités utilisées dans chacune des deux directions
selon les abscisses on mesure avec l'unité OU
selon les ordonnées on mesure avec l'unité OV
on peut représenter un quadrillage selon ces mesures
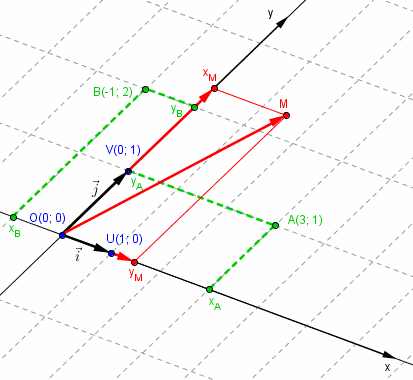
et les coordonnées d'un point c'est les coordonnées sur cette grille.
donc par définition les coordonnées de O sont (0; 0), celles de U (1; 0) et celles de V (0; 1)
On en tire diverses conséquences comme l'obtention des coordonnées en traçant des parallèles aux axes (points xA, yA, xB, yB) et la "relation fondamentale" qui définit les coordonnées d'un point M :
les coordonnées d'un point M sont par définition les nombres x et y tels que
le repère est dit orthogonal si les axes sont perpendiculaires
il est orthonormé si de plus les longueurs OU = OV
c'est à peu près tout ce qu'il y a à savoir sur les systèmes de coordonnées en général
Le reste est des conséquences de ces définitions, comme les diverses formules de calcul de coordonnées (qu'il vaut mieux savoir par coeur pour éviter de les redémontrer à chaque fois)
Ah oui, ça parait beaucoup plus clair, enfait il n'y a même pas besoin de tracer quoi que ce soit pour que A ait pour coordonne (0;1) et B (1;0), car tout point de l'axe des abscisses a une ordonnee egale a 0, et tout point de l'axe des ordonnees a une abscisse egale a 0.
Donc maintenant que je viens de vraiment comprendre l'exercice, il est vrai que la question est un grand nimporte quoi et la seule option est de mettre C en origine.
La question 2 demande un repere orthogonal ( donc que l'axe des ordonnees soit perpendiculaire a l'axe des abscisses) et il manque je pense une information ( que la personne qui a mit l'exercice n'a pas fait) c'est il ne faut pas creer d'autres origines que I sur la figure, et là la question prend tout son sens je crois.
Donc ça m'a donne envie d'en savoir un peu plus sur les reperes de plan, je sais donc que pour connaitre le milieu d'un segment il faut faire la moyenne xM et yM.
Par contre je n'ai pas trop compris l'utilite de la diagonale OM sur la figure.
Merci, encore pour l'eclairage.
sur ma figure le vecteur (pas "la diagonale") = la somme des vecteurs
ce qui est la traduction sur la figure de
le tracé d'un parallélogramme et sa diagonale est la méthode graphique pour additionner deux vecteurs.
parfois on se contente d'un demi parallélogramme = un triangle en mettant les vecteurs bout à bout ce qui exprime "à l'évidence" la relation de Chasles quels que soient A,B,C
ici et comme
...
Et bien pour cette relation j'ai beau cherche, je n'arrive a voir à quoi xMm et Oym peuvent e-etre egales , peut-etre yMm mais, ce n'esr plus de la realion de chasles ?
il y a des indices pas des lettres en vrac.
X indice M : XM est le point sur l'axe des abscisses
tu veux que je te refasse la figure avec des noms sans indices ???
tiens la voila :
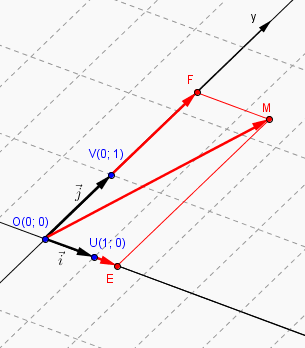
et les relations correspondantes :
ce qui est la traduction sur la figure de
car etc
et avec Chasles
et comme
c'est plus clair comme ça ? c'est la même chose mais avec juste des noms de points sans indices