Inscription / Connexion Nouveau Sujet
exercice de probabilité
EXERCICE:
Bonjour, voici un exercice de probabilité que je n'arrive pas à résoudre en entier, merci de votre aide.
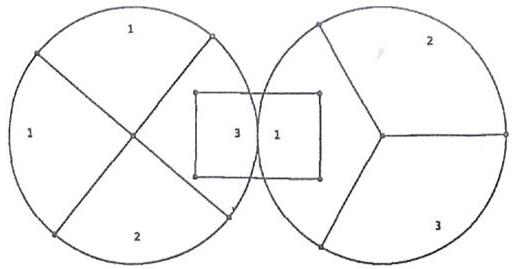
Sur la figure ci-dessus on voit 2 roues de loterie. Celle de droite est partagée en 4 secteurs de même grandeur, avec les numéros 1,1,2 et 3. Celle de gauche a 3 secteurs de même grandeur avec les numéros 1,2 et 3. On fait tourner les 2 roues. On obtient ainsi un couple de 2 numéros qui apparaissent dans le rectangle.On fait la somme de ces 2 numéros.
QUESTIONS/
1) Donner le nombre de couples physiques équiprobables qui peuvent apparaître.
2) Donner les différentes sommes possibles.
3) Quelle est la probabilité d'avoir une somme de 6?
4) Quelle est la probabilité d'avoir une somme de 2?
5) Montrer que la probabilité d'avoir une somme de 4 est de 1/3?
6) Quelle est la probabilité d'avoir une somme au plus égale à 5?
REPONSES/
1) (3;1)/(3;2)/(3;3)/(1;1)/(1;2)/(1;3)/(1;1)/(1;2)/(1;3)/(2,1)/(2;2)/(2;3)
2)4;5;6;2;3;4;2;3;4;3;4;5
3)1/12
4)2/12
5) je ne sais pas comment faire
6) idem
Merci de vos réponses 
Edit Coll : rotation de l'image (pour la troisième fois ! !  )
)
Bonjour,
Comment as-tu fait pour trouver la question 4?
parce que c'est le même principe pour la question 5
Bonjour,
Pour la question 4 j'ai compté le nombre de 2 qu'il y a parmi les autre nombre (12)et comme il y en a que 2 alors c'est 2/12 soit 1/6.
pour la question 5 alors c'est 4/12=1/3.
pour la question 6 alors c'est 3/12=1/4
Merci de votre aide 
Bonsoir choco,
Alors, le début est faux. (1;1) et (2;1) ne sont pas équiprobables !!!. Le premier a une probabilité de 1/6 et le second de 1/12. Donc, reprends moi les couples. Il faut que tu nous trouves deux séries de couple. Le premier avec une probabilité de 1/6 et le second avec une probabilité de 1/12.
2) J'imagine que tu sais faire une somme^^
3) et 4) OK
5) et 6) te seront plus facile si tu nous fait correctement le 1).
(3;1)/(3;2)/(3;3)/(1;1)/(1;2)/(1;3)/(1;1)/(1;2)/(1;3)/
alors est-ce que c'est ça pour les différentes couples qui peuvent apparaître?
Je te recopie la question :
1) Donner le nombre de couples physiques équiprobables qui peuvent apparaître.
Tu ne réponds pas à la question. Mais pour y répondre, donne moi pour chaque couple, la probabilité de l'obtenir.
Ensuite, regroupe ces couples par probabilité et tu pourras donner ce nombre.
A la fin, tu dois donner une réponse de la forme.
On a n couples de probabilité pn et m couples de probabilité pm.


