Inscription / Connexion Nouveau Sujet
EXERCICE : factorisation, développement,et résolution d'équation
Bonjour à tous membre de ilemaths, je suis venu dans ce forum car un ami m'a dit que vous aidez les gens dans les exercices si ils ont des problèmes et fort bien j'ai un problème avec des équations, des factorisations et développement, je ne suis pas ici pour que vous me faites mes exercices mais que vous me corrigez ou dans certains cas m'éclaircir sur la méthode à appliquer.
J'ai auparavant commencer :
PARTIE FACTORISATION
A= 5x4+10x2
A= 5x(x²+2x)
________________________________________
B= (4x-3)(x+1) - (4x-3)(5x-2)
B= (4x-3)(x+1-5x+2)
B= (4x-3)(3-4x)
________________________________________
C= (16x+8)(x-3) + (2x+1)(-3x-5)
C= 8(2x+1)(x-3) + (2x+1)(-3x-5)
C= (2x+1)(8)(x-3-3x+5)
________________________________________
D= (x+3)2 - (2x-4)2
D= (x+3) (x+3) - (2x-4) (2x-4)
Je ne trouve pas de facteur commun.
D= x²+6x+9 - (4x²-16x+16)
D= x²+6x+9 - 4x²+16x-16
D= -3x²+24x-7
________________________________________
E= 9(x+1)² - (3x+2)²
Je ne trouve pas de facteur commun.
________________________________________
F= 25(x-1)² - (3x+2)²
Je ne trouve pas de facteur commun.
________________________________________
DÉVELOPPEMENT
A= -3x(x-4) + 3x²(x+1)
A= -3x²+12+3x3+3x²
A= 3x3+12
________________________________________
B= (x+3)² - (2x-1)(x+5)
B= x²+6x+9 - (2x²+10x-x-5)
B= x²+6x+9 - (2x²+9x-5)
B= x²+6x+9 -2x²-9x+5
B= -x²-3x+14
________________________________________
C= (4x-1)² + (2x-3)(x+2)
C= 16x²-8x+1+2x²+4x-3x-6
C= 18x²-7x-5
________________________________________
D= SOUS FORME IMAGE :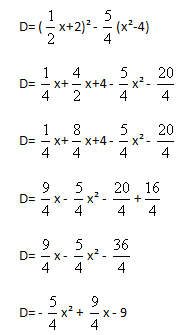
D= SOUS FORME TEXTE :
(1/2x+2)² - 5/4(x²-4)
D= 1/4x + 4/2x + 4 - 5/4x² - 20/4
D= 1/4x + 8/4x + 4 - 5/4x² - 20/4
D= 9/4x - 5/4x² - 20/4 + 16/4
D= 9/4x - 5/4x² - 36/4
D= -5/4x²+ 9/4x - 9
________________________________________
PARTIE EQUATIONS
(1)=> 7(-x+2) - 4(1/2x-1) = -9(x+3)
(1)=> -7x+14 - 2x+4 = -9x-27
(1)=> -9x+18 +27 +9x
(1)=> 45
________________________________________
(2) => (4x+1)² = 9x²
(2) => (4x+1)²-(3x)²=0
(2) =>(4x+1-(3x))(4x+1+(3x)) = 0
(2) => (4x+1-3x)( 4x+1+3x)= 0
(2) =>(x+1)(7x+1) = 0
(2) =>SOIT x+1=0 OU 7x+1=0
(2) =>SOIT x=-1 OU x= -1/7
________________________________________
(3) => 9(-x+3)² = (2x+1)²
(3) => [9(-x+3)-(2x+1)][9(-x+3)+(2x+1)] = 0
(3) =>(-9x+27-2x-1)(-9x+27+2x+1) = 0
(3) =>(-11x+26)(-7x+28) = 0
(3) =>SOIT -11x+26=0 OU -7x+28=0
(3) =>SOIT -11x=-26 OU -7x=-28
(3) =>SOIT x= 26/11 OU x= 28/7
________________________________________
(4) =>(10x+2)(-4+x) = (5x+1)(3x-4)
Je n'arrive pas à équilibrer quand il y a 2 paranthèses de chaque côté.
_______________________________________
a)
SOUS FORME IMAGE : 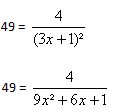
SOUS FORME TEXTE :
49 = 4/(3x+1)²
49 = 4/9x²+6x+1
49(9x²+6x+1) = 4
441x²+294x+49 = 4
441x²+294x+49 - 4 = 0
441x²+294x+45 = 0
Là je ne sais pas comment faire car il faudrait avoir une équation mais je n'arrive pas à le factoriser.
b)SOUS FORME IMAGE : 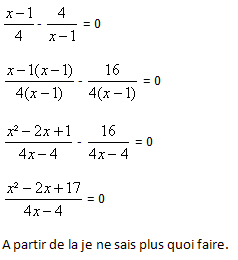
A partir de la je ne sais plus quoi faire.
EDIT : les consignes
PARTIE FACTORISATION : Factoriser les expressions suivantes.
DÉVELOPPEMENT : Développer les expressions suivantes.
PARTIE EQUATIONS : Résoudre les équations
Je crois que pour ça :
E= 9(x+1)² - (3x+2)²
Je ne trouve pas de facteur commun.
________________________________________
F= 25(x-1)² - (3x+2)²
Je ne trouve pas de facteur commun.
________________________________________
C'est plutôt l'identité remarquable a²-b²

Donc ça devrait être :
E= 9(x+1)² - (3x+2)².
E= [9(x²+2x+1)-(9x²+12x+4)][9(x²+2x+1)+(9x²+12x+4)]
E= [9x²+18x+9-9x²-12x-4][9x²+18x+9+9x²+12x+4]
E= (6x+5)(18x²+30x+13)
_______________________________________
F= 25(x-1)² - (3x+2)²
F= [25(x²-2x-1)-(9x²+12x+4)][25(x²-2x-1)+(9x²+12x+4)]
F= [25x²-50x-25-9x²-12x-4][25x²-50x-25+9x²+12x+4]
F= (16x²-62x-29)(34x²-38x-21)
a²-b²=(a+b)(a-b)
E=9(x+1)² - (3x+2)²
E=[9(x+1)+(3x+2)][9(x+1)-(3x+2)]
E=[9x+9+3x+2] [9x+1-3x-2]
E=(12x+11)(6x-1)
J'aurais plutôt fait sa, corrigé moi si c'est faut. :s 
E=9(x+1)² - (3x+2)²
E=[9(x+1)+(3x+2)][9(x+1)-(3x+2)]
E=[9x+9+3x+2] [9x+1-3x-2]
E=(12x+11)(6x-1)
F= 25(x-1)² - (3x+2)²
F= [25(x-1)-(3x+2)][25(x-1)+(3x+2)]
F= [25x-25-3x-2][25x-25+3x+2]
F= (22x-27)(28x-23)
Bonjour
Beaucoup de fautes 
C'est parti pour cette longue correction !
Factorisation :
A = 5x4 + 10x²
A = 5x²(x²+2)
B est juste
C = (16x+8)(x-3) + (2x+1)(-3x-5)
C = 8(2x+1)(x-3) + (2x+1)(-3x-5)
C = (2x+1)[8(x-3)+(-3x-5)]
C = (2x+1)(8x-24-3x-5)
C = (2x+1)(5x-29)
D = (x+3)² - (2x-4)² >>> identité remarquable a² - b² = (a-b)(a+b)
D = [(x+3)-(2x-4)] [(x+3)+(2x-4)]
D = (x+3-2x+4)(x+3+2x-4)
D = (-x+7)(3x-1)
E = 9(x+1)² - (3x+2)²
E = [3(x+1)]² - (3x+2)² >>> identité remarquable a² - b²
E = [3(x+1)-(3x+2)] [3(x+1)+(3x+2)]
E = (3x+3-3x-2)(3x+3+3x+2)
E = 1(6x+5)
E = 6x+5
F = 25(x-1)² - (3x+2)²
F = [5(x-1)]² - (3x+2)² >>> identité remarquable a² - b²
F = [5(x-1)-(3x+2)] [5(x-1)+(3x+2)]
F = (5x-5-3x-2)(5x-5+3x+2)
F = (2x-7)(8x-3)
Développement :
A = -3x(x-4)+3x²(x+1)
A = -3x²+12x+3x3+3x²
A = 3x3+12x
B est juste
C est juste
D = (1/2x+2)² - 5/4(x²-4)
D = (x/2+2)² - 5/4(x²-4)
D = x²/4 + 4x/2 + 4 - 5x²/4 + 20/4
D = -4x²/4 + 2x + 4 + 5
D = -x² + 2x + 9
Equations :
7(-x+2)-4(1/2(x)-1) = -9(x+3)
-7x + 14 - 4/2(x) + 4 = -9x - 27
-7x + 14 - 2x + 4 + 9x + 27 = 0
18 + 27 = 0
45 = 0
Pas de solution
(4x+1)² = 9x²
JUSTE
9(-x+3)² = (2x+1)²
[3(-x+3)]² - (2x+1)² = 0 >>> a²-b²
[3(-x+3)-(2x+1)] [3(-x+3)+(2x+1)] = 0
(-3x+9-2x-1)(-3x+9+2x+1) = 0
(-5x+8)(-x+10) = 0
x = 8/5 OU x = 10
(10x+2)(-4+x) = (5x+1)(3x-4)
2(5x+1)(-4+x) = (5x+1)(3x-4)
2(5x+1)(-4+x) - [(5x+1)(3x-4)] = 0
(5x+1)[2(-4+x)-(3x-4)] = 0
(5x+1)(-8+2x-3x+4) = 0
(5x+1)(-4-x) = 0
x = -1/5 OU x = -4
a)
49 = 4/(3x+1)²
49(3x+1)² = 4
[7(3x+1)]² = 2²
[7(3x+1)]² - 2² = 0 >>> a²-b²
[7(3x+1)-2] (7(3x+1)+2] = 0
(21x + 7 - 2)(21x + 7 + 2) = 0
(21x + 5)(21x + 9) = 0
x = -5/21 OU x = - 3/7
b)
(x-1)/4 - 4/(x-1) = 0
[(x-1)(x-1)]/4(x-1) - 4(4)/4(x-1) = 0
(x-1)(x-1) - 16 = 0
(x-1)² - 4² = 0
(x-1-4)(x-1+4) = 0
(x-5)(x+3) = 0
x = 5 OU x = -3
A vérifier : je ne suis pas à l'abri d'une erreur de calcul ou de faute de frappe


@moomin : Un grand merci, je vais tout de même tout vérifier si une faute de frappe ne soit pas au rendez vous
@girly93 : Je bloquais souvent àcette endroit, merci de m'avoir montrer comment faire avec une identité remarquable.
BONNE CONTINUATION !!

 alors !
alors !
