Inscription / Connexion Nouveau Sujet
Exercice géométrie dans l’espace
Bonjour
Je bloque totalement sur cet exercice pouvez vous m'aider ? Merci
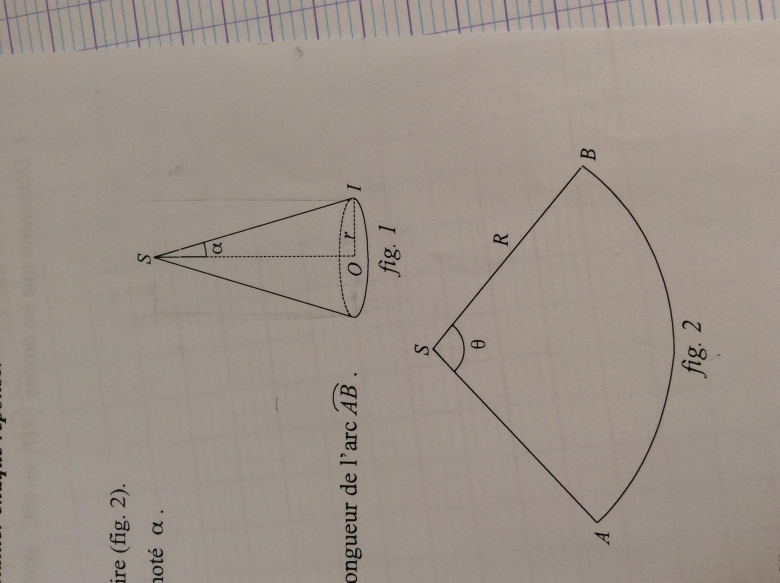
Le patron d'un conne sans la base ( fig.1) et qu'un secteur circulaire (fig.2)
On appelle le demi angle du cône l'angle , En degrés, noter a.
L'angle =
, en degrés, est l'angle du patron. On note R la longueur SB et r la longueur OI
1. Exprimer r en fonction de R et a.
2. Justifier le fait que l'arc AB mesure 2 R
R
3. Écrire l'égalité entre le périmètre de la base du cône et la longueur de l'arc AB .
En déduire l'expression de en fonction de a.
Merci pour votre aide  car je me perd totalement dans cet exercice.
car je me perd totalement dans cet exercice.
Bonjour,
1. Peut être essayer d'appliquer
En considérant SOI rectangle en O
Essaies d'appliquer ce que je t'ai dit ici , sous réserve que SOI est rectangle en O . Qu'est ce que ça donne ?
Exacte , pour rappel = côté opposé à l'angle alpha /l'hypoténus. Du coup réécris bien l'expression du sin(alpha) , ensuite tu remplace par les valeurs données en énoncé...
Ensuite me dire pourquoi tu as affirmé que SI=SB (juste pour savoir si on voit les choses de la même manière sur cette exercice  )
)
Nous pouvons voir que sur la figure 1 il y a S et sur la figure 2 aussi et que fait 360 donc le double de a ?
On te demande quoi dans l'exercice ? Du moins à la question 1.
Exprimer r en fonction de R et qu'est ce que ça veut dire ?
Bonne question ! Je sais pas ! Cette question pour moi sa serait r=(R)= OI+SB
r=(a)=
+OI
Mais je sais que ce n'est pas sa 
La tu compliques les choses , c'est simplement
trouver une expression de r dans laquelle on a R et
Ex: , un autre
Ex:
......
Yen a tellement que tu peux prendre en exemple à la seul condition qu'il y ait et
Mais non !! Avant de répondre, essaies de bien regarder pourquoi t'es si pressée d'aboutir au résultat ?
alors
Petit rappel de 5eme ,4eme
avec , b,d  0
0
En particulier pour b=1 tu as
c=ad
Et maintenant si tu revient au vif du sujet
Oui mais écris sin(a) je comprendrai si tu peux pas écrire
Au lieu de sin , d'accord ? Et la tu viens tant bien que mal d'exprimer r en fonction de R et de
Question ?
prends la peine de bien lire ! Au cas où t'aurai des difficulté à écrire dans le forum dans le cas échéant écris simplement sin(a) je comprendrai que tu as voulu écrire
.
Car :
juste qu'il faut bien écrire. C'était une petite remarque
Je viens de comprendre , désoler mais notre prof nous donnent des DM sur des choses que nous avons jamais appris se qui explique mon incompétence
Ok donc la mesure d'un arc de cercle intercepté par un angle = ( rayon du cercle )X(la mesure de l'angle )
Et comme ta fig2 est un secteur circulaire , si te fais l'image d'un chapeau de noël qui a la forme d'un cône, tu le tiens par le sommet "s" et que tu le fait tourner sur lui même, ce cône décrira un cercle de centre s et de rayon R .
Salut tu as disparu hier  ...
...
Ok revenons en , t'as compris l'histoire du chapeau de noël ? Tu as pu voir le cercle que ça décrit ?
Super ... juste un petit questionnaire.
Un tour de cercle correspond à quel angle ?
En degré = ..?
En radiant= ...??
C'est , en radiant...
Ps: pour passer de degré en radiant comme de radiant en degré tu peux faire une règle de 3 ...
Ce pendant y'a des angles classiques en radiant par exemple dont tu dois avoir leur expression en degré tu dois les avoir par coeur .
Donc tu peux te servir de l'une des 3 relations pour faire une règle de trois pour convertir n'importe quel angle de radiant en degré et de degré en radiant...
Du coup sachant que
(ça ne change rien vu que quand je multiplie n'importe quel nombre non nul par 1 il sera toujours égale à lui même )
Après tu peux juste remarquer que
D'où le résultat demandé...







