Inscription / Connexion Nouveau Sujet
Exercice INTEGRATION - Type bac
Bonjour ! Je me retrouve ici pour recevoir si possible un peu d'aide concernant un exercice type bac sur l'intégration. Je suis en tle STL et j'ai quelques lacunes en mathématiques mais je pense que si quelqu'un peut m'expliquer comment raisonner, etc... Je saurais faire l'exercice (il est un peu long mais je pense qu'en ayant bien tout compris il se fait rapidement).
Merci à l'avance de votre aide. 
(J'ai essayé de répondre à certaines questions mais bon... je ne suis jamais sûre de moi... j'écris alors ce que je pense en vert pour laisser une trace ^^)
Voici l'exercice, avec le graphique en pj.
On considère la fonction f définie sur [1;] par f(x)=2x+1-x ln x
Le plan est muni du repère orthonormé (OIJ). L'unité du graphique est 1cm.
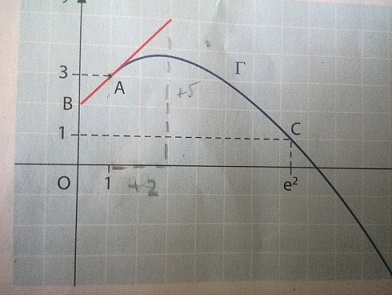
La droite (AB) est tangente à au point A(1;3) et B(0;2)
Le point C(e²;1) appartient à la courbe .
*Déterminer graphiquement f'(1). (f'(1)=3)?
*Résoudre graphiquement sur [1;11] f(x)1. (Malheureusement la calculatrice que j'ai pour le moment donne le résultat final et je ne le comprends pas... f(x)
1
0<x≤e²)
*Expliquer pourquoi f(x)=0 admet une unique solution dont on donnera un encadrement d'amplitude 1.
*Vérifier que pour tout x de [1;limsup] => f(x)=x(2-lnx)+1. (J'ai su le faire  ) .
) .
En déduire lim f(x) en +infini.
*Démontrer que pour tout x de [1;limsup] on a f'(x)= 1-ln(x). (J'ai réussi aussi ^^).
*Résoudre dans [1;limpsup] => 1 - ln(x)0. En déduire le signe de f'(x) sur [1;limsup].
*Etablir le tableau de variation de f.
*Déterminer une équation de la tangente à au point C.
.
.
.
Il reste encore quelques questions et je ne veux pas poster un pavé... Donc si quelqu'un n'est pas trop effrayé à l'idée de devoir m'aider un petit peu (j'essaierai de comprendre au mieux ^^), j'en serai ravie! Et je posterai les dernières questions après avoir fait tout cela ^^.
Merci encore. 
Bonjour !
*Déterminer graphiquement f'(1). (f'(1)=3)?
Non, on ne te demande pas de trouver f(1) mais f'(1) cela correspond à la pente (= coefficient directeur) de la tangente à la courbe au point d'abscisse 1.
Tu vois ? (sur l'image)
Résoudre graphiquement sur [1;11] f(x)
 1.
1.On te demande une résolution graphique. Trace la courbe et regarde pour quelles valeurs de x elle est au dessus de la droite d'équation y = 1
*Expliquer pourquoi f(x)=0 admet une unique solution
Connais tu le théorèmes des valeurs intermédiaires ?
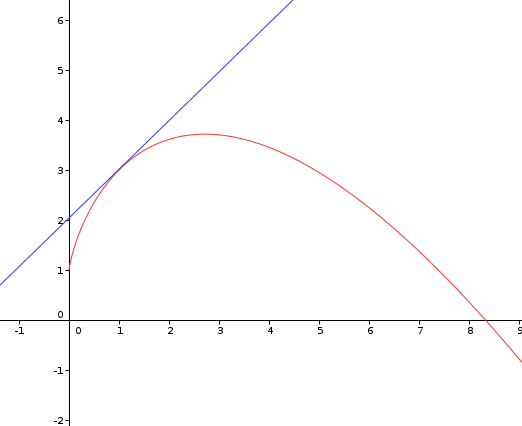
Pardon on a pas la même courbe...
Tu es sûre d'avoir bien recopié ta fonction ? C'est bien f(x)=2x+1-x \times ln(x) ?
Oh non pardon !! Ce n'est pas la fonction qui est fausse mais le graphique, j'ai mis le mauvais en pj.Voici le graphique de l'exercice.
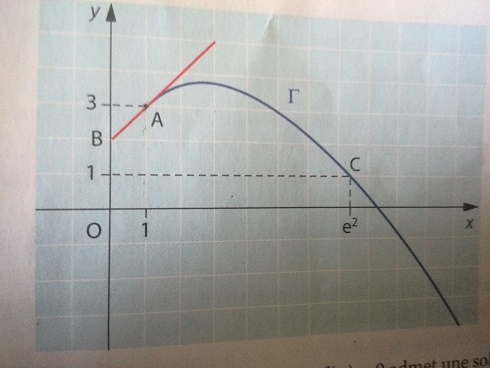
Bien donc on a la même c'est rassurant ! Et ils t'ont même tracé tangente au point d'abscisse 1 et droite d'équation y = 1 ! Tu peux donc répondre aux questions 
Du coup ce n'était pas la bonne courbe mais ma première réponse :
f'(1)=3 est correcte ?
Si je me positionne à x=1 et que je vais jusqu'à la tangente j'ai bien y=3. C'est bien comme ça qu'il faut faire ? f'(1)=3
Pour résoudre f(x)>= 1 graphiquement, je regarde par rapport à la droite d'équation y=1 et à quelles valeurs x ma courbe est au dessus de y=1, je comprends.
Alors, sur mon graphique du coup... les valeurs x vont de 1 à e² c'est bien ça si j'ai bien compris ? Je peux le noter de cette façon ?
Je ne connais pas du tout le théorème des valeurs intermédiaires  .
.
Merci d'avoir répondu aussi vite  !
!
Du coup ce n'était pas la bonne courbe mais ma première réponse :
f'(1)=3 est correcte ?
Si je me positionne à x=1 et que je vais jusqu'à la tangente j'ai bien y=3. C'est bien comme ça qu'il faut faire ? f'(1)=3
Non. Graphiquement tu lis que f(1) = 3 mais nous on veut f'(1) (la dérivée) qui correspond au coefficient directeur (ou la pente) de la tangente qui a été tracée. Comment lire cette pente ?
Alors, sur mon graphique du coup... les valeurs x vont de 1 à e² c'est bien ça si j'ai bien compris ? Je peux le noter de cette façon ?
Oui.
Je ne connais pas du tout le théorème des valeurs intermédiaires .
Je ne sais pas ce qu'ils attendent de toi alors. Peut-être graphiquement encore une fois ?
Non. Graphiquement tu lis que f(1) = 3 mais nous on veut f'(1) (la dérivée) qui correspond au coefficient directeur (ou la pente) de la tangente qui a été tracée. Comment lire cette pente ?
Je suis censé compter non ? ... Par définition f'(1) est le coefficient directeur de la tangente à la courbe
On fait f'(1)= crx comptés en abscisses/ crx comptés en ordonnée pour arriver à la tangente. C'est ça ?

J'ai du mal là ... bêtement ...
Oui c'est ça ! Nombre d'unités verticales sur nombre d'unités horizontales en quelque sorte.
Attention c'est ordonnées sur abscisse pas l'inverse.
Non pas comme ça... Il faut que tu prennes deux points qui appartiennent à la tangente pas deux points au hasard 
Oui par exemple ! Pars de A et va jusqu'à B.
Il faut simplement choisir deux points de la droite. Et c'est plus simple lorsqu'ils ont des coordonnées entières.
D'accord ! Donc simplement, en allant de A vers B, on a x=-1 et y=-1 donc f'(1)=-1/-1 = 1
Donc f'(1) = 1
D'accord !!! Hé bien merci beaucoup, j'ai l'air bête maintenant, quelque chose d'aussi simple ^^'.
Bonne journée 
Oui ^^ La voici :
* Il faut que je détermine une équation de la tangente au point C.
Ici il faut utiliser y=f'(a)(x-a)+f(a) ?
*Il faut remplir un tableau dans lequel les valeurs doivent figurer à 10^-2
| x | 8 | 8,1 | 8,2 | 8,3 | 8,4 | 8,5 |
| f(x) |
*Donner un encadrement d'amplitude 10^-2 de la solution
Calcul d'aire:
*La fonction G est définie sur ]0;+inf[ par G(x) = x²/2 (ln x -1/2). Montrer que G est une primitive de la fonction g par g(x) = x ln x
*Trouver une primitive de F sur f. (Je n'ai pas jamais cherché de primitive avant... elle était toujours donnée pour calculer l'aire...)
*Calculer la valeur exacte en cm² de l'aire de la partie du plan limitée par la courbe, l'axe des abscisses et les deux droites d'équations x=1 et x=e².
*Donner la valeur approchée arrondie à 10^-2 du résultat obtenu précédemment.
Ah je parlais plutôt des questions que tu n'as pas encore faites.
Tu as fait tout ça ?
En déduire lim f(x) en +infini.
*Résoudre dans [1;limpsup] => 1 - ln(x)\geq0. En déduire le signe de f'(x) sur [1;limsup].
*Etablir le tableau de variation de f.
*Déterminer une équation de la tangente à \Gamma au point C.
Alors oui :
*Limite de f(x) = x(2-ln(x))+1
lim f(x) = -inf
x->+inf https://www.ilemaths.net/equation/editor.php?target=corps&phpBB
car : lim x = +inf ; lim 2-ln(x) = -inf ; lim 1 = 1. Donc par opérations sur les limites on a :
+inf * -inf = -inf puis -inf + 1 = -inf.
*1-ln(x)0
-ln(x)
-1
ln(x)
1
e^ln(x)
ln(1)
x
ln(1)
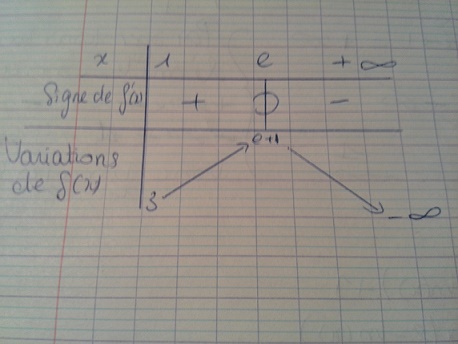
*Tableau de variation de f : en PJ
*Je n'ai pas su déterminer la tangente gamma au point C
Il y a une erreur à la ligne en rouge. Comment passes tu de la ligne précédente à celle-ci ?
Pour la tangente : quelle est l'équation de la tangente à la courbe en un point ? (expression générale, c'est du cours
 )
)d'où ton tableau de variation d'ailleurs. Si ton inéquation était juste ce ne serait pas "e" au milieu mais "ln(1)"
1-ln(x)0
-ln(x)
-1
ln(x)
1
e^ln(x)
e^1
x
e^1
Voilà ! Petite erreur d'inattention ^^
Et pour l'équation d'une tangente on utilise y=f'(a)(x-a)+f(a)
Uhm...l'équation de la tangeante gamma au point C... avec y=f'(a)(x-a)+f(a).. le point d'abscisse A c'est e² non?...
Donc ça serait...y=(e²)*(x-e²)+f(e²) ?
Puis je calcule f'(e²), f(e²), puis je développe dans la formule de la tangente ?
Pas comme moi hein (  j'ai écrit trop vite) : il faut écrire "y =" devant bien sûr sinon ça n'a aucun sens
j'ai écrit trop vite) : il faut écrire "y =" devant bien sûr sinon ça n'a aucun sens
Oui oui bien-sûr j'ai tapé vite moi aussi et j'ai oublié le f ^^.
Alors...
y=f'(e²)(x-e²)+f(e²)
Avec: f'(e²)= 1 - ln(e²) = -1
et f(e²)= e²(2-ln(e²))+1 = 1
Donc on a :
y= -1(x-e²)+1
= -1x * 1e² +1
y=f'(e²)(x-e²)+f(e²)
Avec: f'(e²)= 1 - ln(e²) = -1
et f(e²)= e²(2-ln(e²))+1 = 1
Donc on a :
y= -1(x-e²)+1
Oui
= -1x * 1e² +1
Non :p Attention à ton développement.
Yes!
J'ai pu m'avancer un peu et là j'en suis à la primitive, je dois montrer que
G(x)=x²/2(lnx-1/2) est la primitive de g(x)=xlnx.
Je sais que pour le montrer il faut dériver la primitive, mais je n'arrive pas appliquer mes formules 
Oui il faut bien dériver G et vérifier que sa dérivée est g.
Si tu n'arrives pas à appliquer directement tes formules, décompose.
Pose
et complète :
enfin, trouve la dérivée avec la formule :
Merci ^^
Alors... : u(x)= x²; u'(x)=2x
v(x)=2(ln(x)-1/2); v'(x)= 2x
(v(x)=(-1+2*ln(x))
Enfin... en utilisant (u/v)' j'ai:
=2x * (2(ln(x)-1/2) - x² *(2/x) / (2(ln(x)-1/2)²
=4x * ln(x) -2x -2x / (2(ln(x)-1/2)²
=4x*ln(x) -4x /(2(ln(x)-1/2)²
Heu ... 
Dis moi avant tout :
ce ne serait pas plutôt :
?
Parce que ce n'est pas ce que tu avais écrit (problème de parenthèse) et que ça ça te mènerait au bon résultat.
Mais ce coup ci plutôt avec
et
v(x)=2(ln(x)-1/2) et v'(x)=2(1/x) soit 2*1/x = 2/x
Ben 2*1/x=2x
Mais vu que tu t'es trompée en recopiant ta fonction G, on recommence et on dérive la bonne forme

Ok, on a u(x)=x², u'(x)=2x. v(x)=2(ln(x)-1/2), v'(x)= 2x.
On utilise (u/v)' = u'v - uv'/(v)²
On a alors :
g'(x) = 2x * (2(ln(x)-1/2) - x² * (2x) / (2(ln(x)-1/2)².
Jusqu'ici c'est bon ?
v'(x)= 2x.
c'est 2/x ! Tu vois pourquoi ?
Et puis non recommence avec la bonne fonction (celle de mon message de 15h19) parce que là tu appliques la formule de la dérivée d'un quotient alors qu'on veut la dérivée d'un produit (la bonne formule est écrite dans mon message).
G(x) c'est bien x²/2 * ( ln(x)-1/2)
Désolée je fais encore la même erreur !! >< je commence à fatiguer..
G(x) c'est bien x²/2 * ( ln(x)-1/2)
Non. Là tu as écris :
La bonne fonction s'écrit G(x)=(x²/2) * ( ln(x)-1/2)
c'est à dire
et en dérivant cette fonction tu aboutiras
Bon.. une dernière fois et c'est la bonne ...
Je pars de G(x)=x²/2(ln(x)-1/2),
d'abord j'ai u(x)=x²/2, u'(x)=x. v(x)=ln(x)-1/2, v'(x)=1/x
J'utilise la formule (uv)' = u'v+uv', ce qui me donne:
g'(x) = x * (ln(x)-1/2) + x²/2* (1/x)
= x*ln(x)-x/2 +x/2
= xlnx !!!