Inscription / Connexion Nouveau Sujet
Exercice math géométrie
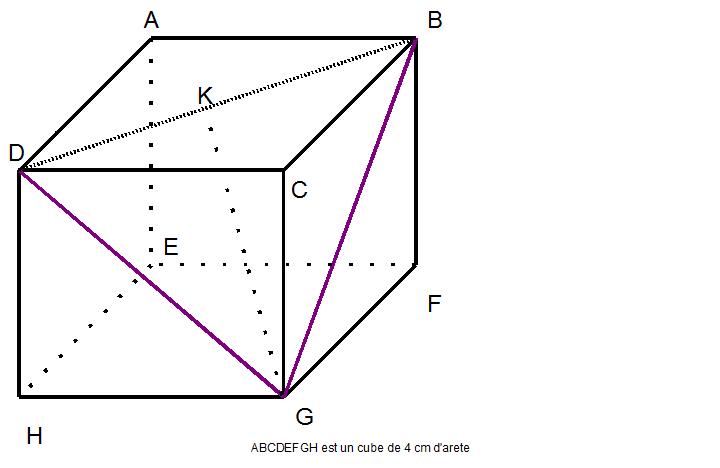
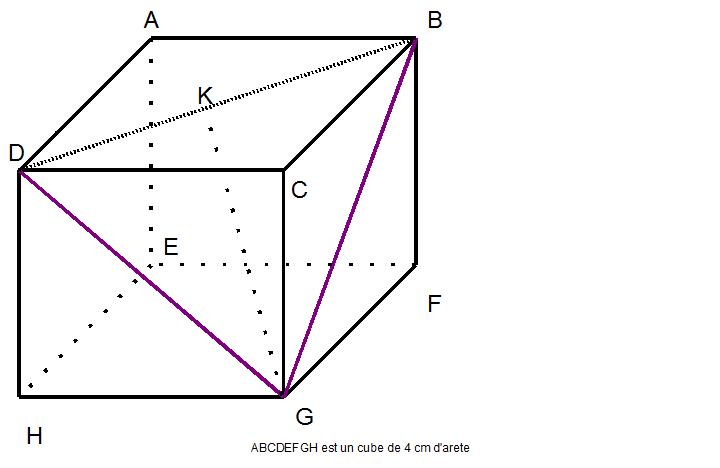
ABCDEFGH est un cube de 4 cm d'arête K est perpendiculaire a (DB)
a. Calcule la valeur exacte de GD et écris le
résultat sous la forme a 2 avec a entier.
b. Quel est le périmètre du triangle BDG ?
Tu donneras la réponse sous la forme a 2.
c. Calcule la valeur exacte de GK.
d. Calcule l'aire du triangle BGD.
Donne la valeur exacte puis une valeur arrondie
au centième.
bonjour,
GD² = DH²+HG²=
GD² = 4²+4² =
GD² = 16+16
GD² =32
GD = 5,65
GD = 4V2
GD est la diagonale du carre ABCD et la diagonale d'un carre= cV2
GD est l'hypoténuse dans le triangle GDC rectangle en C. Or tu sais que CD et GC sont égale à 4 puisque ce sont des arêtes du cube donc tu as : GD²= GC²+DC²
= 4² +4²
= 32
Donc GD =  32 =
32 =  16 x
16 x  2 = 4
2 = 4 2
2
Merçi beaucoup pour cette première réponse .
b) Calculez le perimetre du triange BDG
Je fais comment svp ?
Je ne sais pas comment m'y prendre .
b) DG=DB=GB=4 2 puisque ce sont chacun des diagonales d'un carré.
2 puisque ce sont chacun des diagonales d'un carré.
Le périmètre du triangle DGB est donc égale à 3x4 2 = 12
2 = 12 2
2
Bonjour.
[GK] est l'hypoténuse du triangle rectangle GCK.
GC² = 4² = 16
CK = CA/2 = CD* 2 / 2 = 4*
2 / 2 = 4* 2 / 2 = 2
2 / 2 = 2 2; CK³ = 4*2 = 8
2; CK³ = 4*2 = 8
GK² = GC²+CK² = 16*8 = 24
GK =  24
24
aire du triangle BGD = BD * GK /2
Bonjour ,
BCDEFGH est un cube de 4 cm d'arête K est perpendiculaire a (DB)
a. Calcule la valeur exacte de GD et écris le
résultat sous la forme a 2 avec a entier.
Le cube contient des faces carrés donc ses diagonale sont de même longueur et se coupe en leur milieu et chaques face a 4 angles droits .
Dans le triangle CDG , rectangle en C , d'après le théorème de Pythagore , GD²=DH²+HG²
GD²=4²+4² etc .. GD² = 4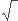 2
2
b. Quel est le périmètre du triangle BDG ?
GD=GB=DB car les diagonales sont de même longeur . Donc GBD est un triangle équilatéral .
Pbdg = 3 X 4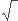 2 = 12
2 = 12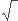 2
2
Tu donneras la réponse sous la forme a 2.
c. Calcule la valeur exacte de GK.
C'est là ou je ne sais pas comment faire .
Je sais juste c'est que GK est une hauteur car elle part d'un sommet et est perpendiculaire a la droite opposé .
Mais je ne sais pas si c'est de cela qu'on peut partir .
d. Calcule l'aire du triangle BGD.
Donne la valeur exacte puis une valeur arrondie
au centième.
*** message déplacé ***
Bonjour ,
BCDEFGH est un cube de 4 cm d'arête K est perpendiculaire a (DB)
a. Calcule la valeur exacte de GD et écris le
résultat sous la forme a 2 avec a entier.
= Le cube contient des faces carrés donc ses diagonale sont de même longueur et se coupe en leur milieu et chaques face a 4 angles droits .
Dans le triangle CDG , rectangle en C , d'après le théorème de Pythagore , GD²=DH²+HG²
GD²=4²+4² etc .. GD² = 4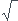 2
2
b. Quel est le périmètre du triangle BDG ?
GD=GB=DB car les diagonales sont de même longeur . Donc GBD est un triangle équilatéral .
Pbdg = 3 X 4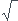 2 = 12
2 = 12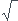 2
2
Tu donneras la réponse sous la forme a 2.
c. Calcule la valeur exacte de GK.
C'est là ou je ne sais pas comment faire .
Je sais juste c'est que GK est une hauteur car elle part d'un sommet et est perpendiculaire a la droite opposé .
Mais je ne sais pas si c'est de cela qu'on peut partir .
d. Calcule l'aire du triangle BGD.
Donne la valeur exacte puis une valeur arrondie
au centième.
*** message déplacé ***
bonjour,
t'as deja posté cet exo le 13/12 et on t'a repondu plumemeteore t'as tout ecrit relis sa reponse sur ton premier post
*** message déplacé ***
Oui mais le GK , j'ai pas compris car je n'arrive pas a prouvé que GCK est rectangle en C .
*** message déplacé ***
fais gaffe tu fais du multi-post ca fait 3 fois que tu postes le meme exo regarde ce que je t'ai repondu
*** message déplacé ***
on peut pas supprime il fallait faire remonter ton premier post en posant une ?
*** message déplacé ***
Bonjour
BGD est un triangle équilatéral dont la longueur d'un côté est 2 2
2
or si tu as un triangle équilatéral de côté a, la longueur de l'une des hauteurs est de a 3/2
3/2
pour le démontrer, tu peux, ou te servir de Pythagore, ou du sinus de l'angle de 60°, et en pensant que le pied d'une hauteur est au milieu du côté opposé
*** message déplacé ***



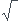 2
2
