Bonjour, un petit effort ! les instructions sont super simples à comprendre, tu n'as pas besoin de savoir programmer pour comprendre ce que fait cet algorithme.

Qu'est-ce que tu proposes ?

Bonjour
[ déja dit par Glapion, rien à rajouter ]

nota : plutot que d'écrire des trucs faux avec un caractère spécial qui n'est pas le bon
pour écrire un exposant il est mieux d'écrire x^3 que x³ ou pire que x² faux

Pour la 1 il faut raccourcir le A et le B ?
Pour la 2 c'est vérifié si il y a égalité entre A et B ?
Pour la 3 on calcul A et B
Et pour la 4 on développe le côté gauche puis on calcul pour faire la conclusion ?

Bonsoir,

En dehors du fait, relevé par mathafou, que l'égalité en question 4 est hors de la syntaxe de Python, il est bon de signaler que ;

x*x*x est évalué en tant qu'entier si x est entier
x^3 (x**3 en syntaxe Python, x³ en notation courante ) est évalué en tant que double même si x est entier
On ne compare qu'avec précaution des entiers avec des doubles, même si Python s'exécute avec un typage dynamique

Cet aparté ne change pas la réponse à donner à la question 4.

Je ne comprends pas vraiment la question 1, voir pas du tout, après pour la 2 et 3 j'ai trouvé il n'y a pas de problème
La 2 il suffit de dire que ce programme montre si il y a une égalité
Et le trois il suffit de tout calculer

ce que je relevais n'a rien à voir avec Python
c'est l'écriture incorrecte en pur texte d'une formule par utilisation d'un caractère spécial illisible et faux

la 1 "Je ne comprends pas vraiment" parce que tu cherches 1000 fois plus compliqué que ce qu'on te demande vraiment : de traduire en langage mathématique sans rien développer, juste de la traduction de syntaxe

par exemple
A = (x-2)*(x+1)*(x+1)*(3-2*x) c'est du langage Python

ça veut dire "en langage mathématique" la formule
A = (x-2)(x+1)(x+1)(3-2x) point final

pareil pour l'autre, que veut dire d'un point de vue mathématique calculer le produit x*x*x ?
etc

la 2 oui c'est ça : le programme dit s'il y a égalité entre ces deux calculs pour cette valeur de x qu'on lui a fournie

la 3 effectivement c'est les calculs, à effectuer tels qu'ils sont "définis", littéralement.
(ou faire tourner le programme sur Python)

la 4 c'est justifier si oui ou non la vérification de l'égalité de ces quelques valeurs prouve ou pas que les deux formules seraient "égales" quel que soit x

On pourrait écrire A = (x-2)(x+1)²(3-2x)

Et B = 2x³+5x²+x-6

voila c'est ça la réponse à la question 1

(et tu remarques que comme par hasard c'est les deux formules de la question 4 ! )

Oui c'est bon j'ai réussi merci bcp !

Bonjour, j'ai attentivement suivi vos échanges.

Malgré ma méconnaissance de Python (mais je me soigne ), j'aurais su répondre aux questions posées .

Cependant, je souhaite faire part de 3 remarques :

1) j'ai trouvé bien décevant (frustrant) que ce bout de code ne débouche pas sur sa mise en oeuvre... exécution !
J'ai donc complété et testé (2 lignes suffisent) : élémentaire (quand on sait !!)

2) J'ai remarqué que le code présenté dans cet exercice, utilise une "fonction" (j'ai cru comprendre que cela est à la mode, sinon très important). Soit. Mais alors, je n'ai pas compris l'intérêt des return qui renvoient dans tous les cas.... la valeur de x que l'on a rentrée !

3) J'ai découvert l'importance des indentations dans Python. Dur dur au début...

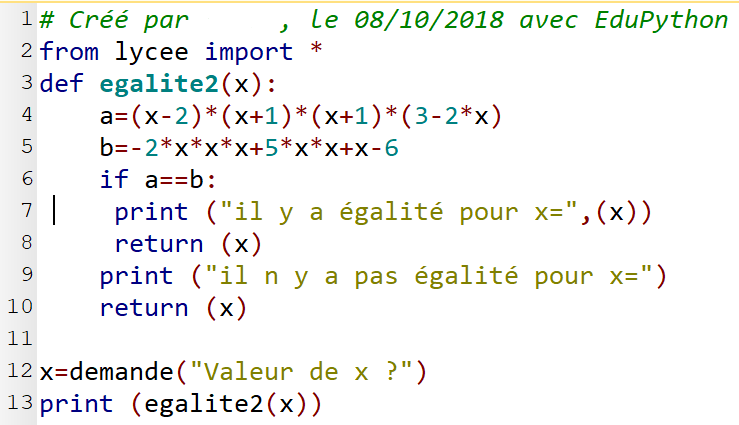
Bonjour ZEDMAT
mettre du texte (c'est du texte !!) en image, c'est pas sympa pour ceux qui voudraient citer des morceaux pour les commenter : ils sont obligés de les retaper !
alors que du texte depuis la fenêtre Python ça se copie en tant que texte et ça se colle ici en tant que texte !

tu as rajouté l'affichage de la valeur de x dans le premier print et pas dans le second
et tu le réimprimes à la fin dans le print(égalité2(x)) puisque le résultat (le return) de la fonction égalité2(x) c'est x dans tous les cas

c'est un peu incohérent et ça conduit à un double affichage de la valeur x dans le cas d'égalité

Petites remarques de détail : le x renvoyé depuis le sous programme ne sert à rien, les print intéressants sont dans le sous programme, on pourrait avoir des return() ça ne changerait rien, le print (egalite2(x)) ne sert pas à grand chose en fait. Et ça affiche deux fois x si on a égalité. on pourrait appeler la fonction en faisant simplement egalite2(x)

une dernière remarque tant qu'à faire :

sans "import" et sans ligne supplémentaires ni aucune modif du programme d'origine :

def egalite2(x):
A=(x-2)*(x+1)*(x+1)*(3-2*x)
B=-2*x*x*x+5*x*x+x-6
if A==B:
print("il y a égalité pour x=")
return(x)
print("il n'y a pas égalité pour x=")
return(x)

ça suffit pour exécuter effectivement tout ça

une fois ce "programme" lancé on a dans la Console Python (en bas de la fenêtre de EduPython) la possibilité de tester et de voir les résultats directement :

*** Console de processus distant Réinitialisée ***
>>>
>>> egalite2(0)
il y a égalité pour x=
0
>>> egalite2(-1)
il y a égalité pour x=
-1
>>> etc

salut,
si l'algo repond à la question: x est-il solution de l'equation alors
le programme devrait à mon sens renvoyer
vrai si x est solution
faux si x ne l'est pas.

Quant à la fonction je serais tente de la nommer est_solution

faut pas réinventer un autre exo

l'algo répond à la question "les deux expressions donnent la même valeur ou pas pour cette valeur de x en entrée"
et c'est cohérent avec les questions
3. .
x=-1 oui
x=3/2 oui
x=0 oui

4. Peut on en conclure que, pour tout réel x, (x-2)(x+1)²(3-2x)=-2x²+5x²+x-6? Justifier.
que deux expressions qui prennent la même valeur pour quelques valeurs de la variable sont équivalentes ou pas ?
c'est ça le fond de l'exo.
pas de résoudre je ne sais quoi.

et le but est raté parce que pour x = -2 ... .bof
faute de frappe dans l'énoncé ? (x = +2)
ou réponse attendue triviale et sans intérêt parce que pour x = -2 il n'y a pas égalité entre les deux valeurs obtenues, et donc les deux expressions ne peuvent pas être équivalentes, justifiée par ce seul test de x = -2 ?

il n'est pas question de "solutions" là dedans...
mais de savoir si oui ou non deux expressions sont égales quel que soit x, si deux expressions sont équivalentes

l'algo répond à la question "les deux expressions donnent la même valeur ou pas pour cette valeur de x en entrée"

je ne vois pas la difference avec "x est solution ou pas de A=B"

parce que considérer A=B comme une équation n'a aucun rapport avec la formulation de la question 4 qui demande si les expressions A et B sont équivalentes (c'est à dire prennent la même valeur quel que soit x)
et le but de l'algorithme, est précisément de répondre à cette question telle qu'elle est posée et pas réinterprétée autrement.

c'est quoi des expressions equivalentes ?
soit mais une fonction qui retourne son argument ce n'est pas banal ...

en fait elle retourne son argument pour que quand on l'appelle à partir de la console ce soit la valeur de x qui s'affiche après l'impression explicite de "nya nya nya x ="

c'est particulièrement maladroit je suis d'accord.

bien plus sain est :
def egalite2(x):
A=(x-2)*(x+1)*(x+1)*(3-2*x)
B=-2*x*x*x+5*x*x+x-6
if A==B:
print("il y a égalité pour x=",x)
return
print("il n'y a pas égalité pour x=",x)
return

return rien du tout, même pas return()
et affichage de la valeur de x là où on affiche tout ce qu'on a à dire
pas en jouant sur des effets de bord de la console Python qui affiche ce que retourne une fonction quand on l'invoque
et qui de plus est franchement moche, de mettre cette valeur de x sur la ligne d'après :

>>> egalite2(-1)
il y a égalité pour x=
-1
>>>

au lieu de
>>> egalite2(-1)
il y a égalité pour x= -1
>>>
avec le x dans le print.

des expressions équivalentes c'est une identité
(a+b)²
est une expression équivalente à a² + 2ab +b²
on peut partout utiliser l'une ou l'autre ce sera pareil.
parce que ça donne la même valeur quels que soient a et b

bien entendu les deux expressions A et B de l'exo ne sont pas équivalentes (y a qu'à regarder les degrés !)
mais c'est bien ce que demande la question 4, de répondre et de justifier si elles le sont ou pas.
au vu (en déduire) des seuls résultats numériques de la question 3.

je ne saisis pas la nuance entre egales et equivalentes pour des expressions.

Quant au programme autant mettre
...
return true
...
return false

pour avoir une fonction et pas seulement une procedure d'affichage

Merci à vous tous et en particulier à Mathafou. J'ai compris quelques pythoneries supplémentaires et je m'endormirai un peu moins bête ignorant ce soir.