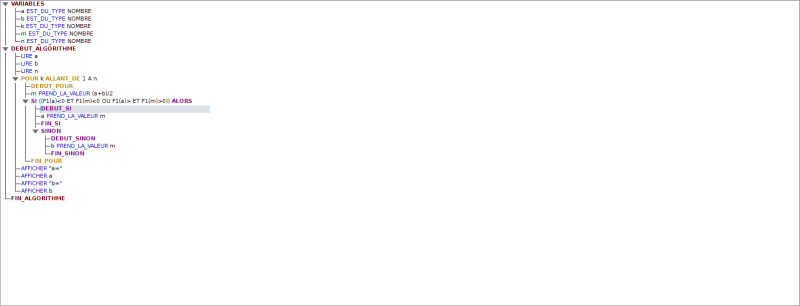Comme indiqué, c'est dû à une erreur de syntaxe.
Si tu nous montres ton code, on te dira ce qui ne va pas.

Voici mon algorithme :

je ne vois pas très bien, mais tes parenthèses dans l'instruction SI ne doivent pas être correctes ; écris bien ( (... ET ....) OU (.... ET ....) )

Ceci dit tu aurais plus vite fait de tester F1(a)*F1(m)
si c'est négatif c'est que la solution de F1(x)=0 est entre a et m et sinon c'est qu'elle est entre m et b.

Je viens de régler le problème il était causé par le Si, merci

j'aurai juste voulu savoir a quoi servait cette algorithme ?

svp

c'est un algorithme de dichotomies successives qui cherche à trouver la valeur de x qui annule la fonction F1(x).

On repère un intervalle [a;b] dans lequel on sait que la solution se trouve parce que la fonction change de signe. On teste le point milieu m=(a+b)/2, on teste si la fonction continue à changer de signe entre a et m si oui on garde l'intervalle [a;m] et sinon on prend l'intervalle [b;m]. Au final on a divisé par 2 l'intervalle. On réessaye le processus n fois et du coup on cerne la racine de beaucoup plus près.