Inscription / Connexion Nouveau Sujet
Exercice sur Géométrie dans l'éspace
Bonjour, à toute et à tous, je suis bloqué sur un exercice je suis sur tout bête mais j'y ai passé déjà plusieurs heures en m'aidant de gégogébra également.
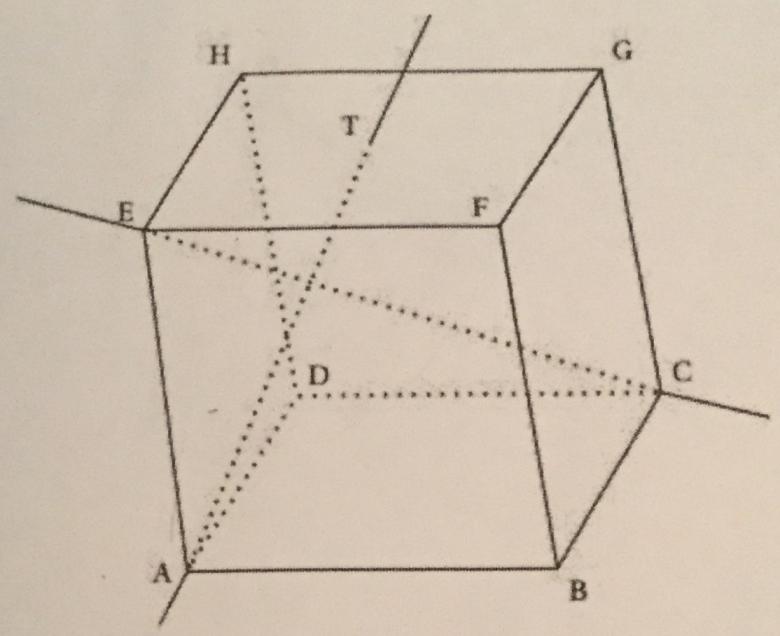
ABCDEFGH est un cube où le point T est le milieu du segment [HF].
1) Démontrer que les droites (EC) et (AH) sont orthogonales.
On admet que la droite (EC) est orthogonale au plan (AHF).
2) Démontrer que les droites (EC) est orthogonale au plan (AHF).
Pour la seconde question il n'ya a pas de soucis car comme (EC) est orthogonal au plan (AHF) j'ai prouver qu'elle était orthogonal à (AT).
Mais pour la première, j'ai die que comme (EC) est orthogonal au plan (AHF) elle était orthogonal a (AH) sauf que mon prof m'a dit que c'était valable pour la seconde question. Donc je suis un peu embrouillé.
Voilà la figure :
Merci d'avance !
Léandre
Bonjour merci de votre réponse !
J'avais pensé à ce plan mais pour prouver qu'une droite est orthogonal à un plan, elle doit être orthogonal à deux droites de ce plan. Et la je sais pas lesquelles prendre. J'ai observé ca sur géogébra et je ne savais pas comment le démontrer.
Dans le plan (ECD) la droite (ED) perpendiculaire à AH est incluse dans le plan (ECD) mais je ne suis pas sur que ca suffise.
Voyons:
(les diagonales d'un carré).
et est perpendiculaire au plan
donc orthogonale à toute droite de ce plan, en particulier
Du coup, est orthogonale à deux droites sécantes
et
du plan
donc perpendiculaire à ce plan.

Merci beaucoup ! Je n'avais pas vue les chose dans cette angle là. J'ai vraiment du mal avec la géométrie dans l'espace. Je préfère tellement l'algèbre…
Bonne journée !
Bonjour,
moi je trouve gonflé de donner un énoncé
1) Démontrer que les droites (EC) et (AH) sont orthogonales.
On admet que la droite (EC) est orthogonale au plan (AHF).
et de refuser une solution qui utiliserait le "on admet que" donné dans l'énoncé !
il n'y aurait pas eu de problème si ce "on admet" loufoque n'avait pas été dans l'énoncé du tout ...
en fait avec ce "on admet" c'est tout l'exo qui est forcé de tourner en rond vu que pour le prouver logiquement question 2, tel qu'est l'énoncé, on est amené à partir du fait qu'on commence par admettre le résultat qu'on veut prouver
donc jeter ce "on admet" aux orties (voire pire, le prof ayant concocté cet énoncé) et faire comme dit parlake est effectivement une saine méthode.

 .
.

