Inscription / Connexion Nouveau Sujet
Exercice sur la dérivée
Bonsoir à tous,
J'ai un exercice de Mathématiques à faire pour Lundi 20 Janvier 2014.
Cependant, j'ai été effrayée par le sujet, de ce fait, je n'arrive pas à le faire ... 
Voici l'énoncé:
"On considère les fonctions fet g définies sur [-1 ; +[ par :
f(x) = et g(x) = 1 +
-
1. Calculer f(0) et g(0)
2. Démontrer que pour les courbes représentatives de ces deux fonctions admettent la même tangente au point A d'abscisse 0.
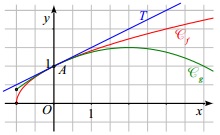
3. On a représenté graphiquement, ci-contre, les fonctions f et g (notée respectivement Cf et Cg), dans un repère orthonormé, ainsi que leur tangente commune T au point A.
On pose, pour tout réel x -1 : d(x) = f(x)-g(x)
-1 : d(x) = f(x)-g(x)
a) Montrer que, pour tout x>-1 :
d'(x) =
b) Etudier, sur l'intervalle ]-1;+[, les variations de la fonction h : x
 2 + (x-2)
2 + (x-2)
c) En déduire que, pour tout réel x>-1, d'(x) 0
0
4.a) Calculer la limite en + de la fonction d
b) Dresser le tableau de variation de la fonction d.
5. Déduire des questions précédentes, les positions relatives des courbes représentatives Cf et Cg."
Pour la question 1. j'ai trouvé f(0) = 1 et g(0) = 1
Pour la question 2. j'ai dit que les deux fonctions vues dans la question 1. possédées toutes les deux le point 1 d'abscisse 0
Pour la question 3.a) je n'arrive pas à trouver d(x) ... Du coup, ça me bloque pour les autres questions ... Dès que j'aurais d(x) je pourrais donc prouver d'(x) et ensuite faire la suite de l'exercice 
Merci aux personnes qui m'aideront! 
Bonjour
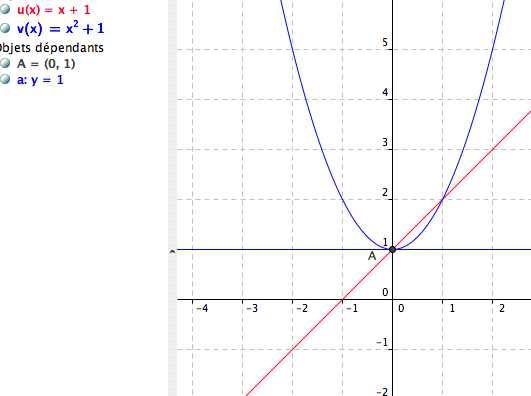
si u(x) = x+1 et v(x) = x² + 1 ,
On a bien u(0) = v(0) = 1 et pourtant les courbes représentant les fonctions u et v ne possèdent pas la même tangente au point d'abscisse 0 .....
TA DEMONSTRATION NE DEMONTRE RIEN !
Quelle démarche mathématiques faut-il faire quand on parle de tangente à la courbe représentant une fonction ?
Exemple fort mal choisi .....
une èquation de la tangente en A à courbe représentant u est y = 1
une èquation de la tangente en A à courbe représentant v est y = 1
....
un autre exemple mieux choisi
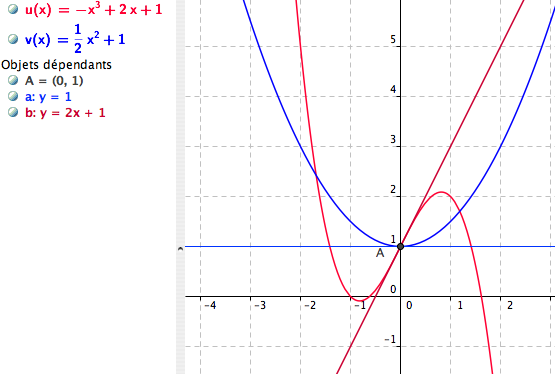
Pour la tangente, est-ce que l'on peut appeler ça "asymptote"? C'est la seule chose que je vois dans mon cours qui pourrait me servir 
Dois-je calculer la dérivée de chaque fonction? Afin de trouver le point commun des deux fonctions? 
la notion d'asymptote ... cela se voit dans le chapitre limite ...
la notion de tangente ... cela se voit dans le chapitre dérivée en 1ère ...
Alors entre les 2 tu choisis quoi ? On joue au poker ou on fait des maths ?
Bonjour,
1) Je trouve g(0)=1 et f(0)=1
2) J'ai fait les dérivées de f et g et je trouve f'(x)=1/(2 x+1) et g'(x)=(1/2)-(1x/4)
x+1) et g'(x)=(1/2)-(1x/4)
Ensuite je me suis servi de l'équation de la tangente : y=f'(a)(x-a)+f(a) et pour les deux courbes je trouve Ta:y=(1x/2)+1
Merci nonofurious de ton aide, cependant, ne doit-on pas enlever le " +1 " pour f'(x) = ?
Je suis perdue... 
enlever un 1 en maths ! cela se saurait
du genre  (1 + 3) =
(1 + 3) =  4 = 2
4 = 2
Et smb]racine[/smb](3) est différent de 2 ou 1 ... En maths on n'a pas le droit au blanco ;
on passe d'une ligne à l'autre avec un calcul possible !
* multiplier les 2 termes d'une égalité par un même nombre
* additionner aux 2 termes d'une égalité le un même nombre
Oui, mais là, c'est par rapport à la dérivée, quand on a f(x)= xa + b, la dérivée de cette fonction est : f'(x)= a, non? 
Et donc, je ne comprends pas pourquoi on garde le " +1 " qui correspond à " b " dans la dérivée de f(x)=
Parce que là f(x) n'est pas de la forme ax + b mais de la forme
f(x) =
Et en France on voit sa dérivée en Terminale !
...
Tu habites quel pays ?
Que dit ton cours ?
Si f =  u alors f' = ....
u alors f' = ....
Ici u(x) = .... et 4'(x) = ....
Avec ce si t4 devrais comprendre !
Je n'ai pas vraiment de cours sur la dérivée, juste un formulaire présentant toutes les dérivées de f possibles.
Si j'ai bien compris:
f(x)= , on a f'(x)=
Ici, u(x) = , donc u'(x) =
Sauf que si f(x) =  (x+1) =
(x+1) =  u(x) ... que vaut u(x) et '(x)
u(x) ... que vaut u(x) et '(x)
donc
Relire son cours cela sert parfois beaucoup !
Bon, j'ai compris maintenant la réponse de nonofurious! 
Merci @jeveuxbientaider! 
Par contre, pour g'(x), je suis à nouveau perdue, car je n'ai jamais vu avec un entier comme dénominateur ...