Bonsoir, je viens par la présente, solliciter votre aide pour la résolution de cet exercice.Bonne reception, merci d'avance.

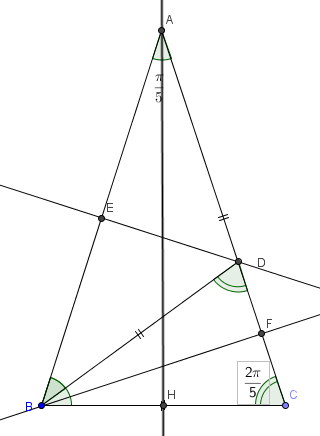
Soit ABC un triangle isocèle de sommet A tel que BC= a et (vec{BA} , vec{BC})=2π/5. La bissectrice de hat{ABC coupe le côté du segment AC en D. Faire une figure
1- Démontrer que AD=BD=a
2- Démontrer que AB= 2a cos π/5 et CD= 2a cos 2π/5
en déduire que cos π/5 - cos 2π/5=1/2
3- On appel H le projeté orthogonal de A sur le segment BC. Calculer BH en fonction de a de deux manières différentes et en déduire que cos π/5 * cos 2π/5= 1/4
4- En remarquant que (x+y)²=(x-y)²+4xy et des réponses précédentes, déduire le système suivant:

cos π/5+ cos 2π/5= (√5)/2
cos π/5- cos 2π/5= 1/2

et calculer cos π/5 et cos 2π/5

5- calculer sin π/5 et sin 2π/5