Bonsoir,
si tu appelles la longueur AB, tu peux exprimer l'aire totale de la pyramide en fonction de .

Bonsoir,
Oui mais l'aire totale est déjà donnée c'est 50m2.

Justement, essaie de prouver que l'aire totale est égale à , ensuite tu devras résoudre l'équation

Je pense que tu as dût trouver cette formule en faisant la question 11. Je suppose que tu dois utiliser le tableur.

Oui sauf dans les premieres questions se sont des mesures au hasard que j'ai mis car on ne me donne pas de mesure precise s mais l'aire totale est donner dans la question ;
Sinon je pensais faire 50:5=10
Or l'aire d'un carre est cxc donc 10:2=5

Ai-ce vrai?

l'aire d'un carré est bien , et ici le côté est AB.
L'aire d'un triangle est , ici la base est AB mais il faut trouver la hauteur en utilisant le théorème de Pythagore.
Dans la cellule B3 tu dois entrer une formule comme =(...)*B1
avec ce qu'il faut à la place des points de suspension. Dans cette formule B1 désigne la longueur AB.

je suis bien d'accord que bxh/2 est l'aire d'un triangle mais je n'ai pas de longueur du triangle pour cacluler la hauteur et B1 designe la longueur de AB avec les mesure que j'ai mise au hasard vue qu'on ne me donne aucune mesure

Et ici la base  est ABCD qui est un carre.
Et pour la premiere formule que vous m'avez donne je ne la comprends pas.

Bonjour,

de toute façon dans cet exo il n'y a pas grand chose à calculer !
ni même de "x" ni de racines carrées de quoi que ce soit ni de Pythagore "en valeurs"

c'est exclusivement "jouer avec Geogebra" pour se familiariser avec ce logiciel et rigoureusement rien d'autre

la "mesure" d'un segment .... on ne la calcule pas !! et elle n'est pas non plus "donnée" (inutile de l'attendre en geignant "je n'ai pas de mesures")
c'est Geogebra qui la mesure pour vous !
dans les "formules" de Geogebra attendues, ce qu'il faut taper c'est des noms d'éléments de la figure

si un segment s'appelle "a" (par exemple le côté du carré)
la formule pour en calculer l'aire, à taper au besoin dans une case du tableur c'est a*a ou a² ou a^2 selon ce qu'on préfère écrire, et écrit textuellement comme ça
on le fait juste précéder d'un "=" pour dire à Géogébra : "calculez moi la valeur de ça" : =a*a


la seule difficulté est la question 4 dans laquelle il faut identifier "sur le patron" et la construction de ce patron, quel élément peut bien être la hauteur de la pyramide !!

sinon quand on demande "pour quelle valeur", eh bien on déplace à la souris les éléments de la figure dynamique qu'on a construite et on regarde dans les cases du tableur, jusqu'à obtenir ce qu'on voulait comme résultat.
c'est tout.

Merci à mathafou, je n'avais pas compris qu'on utilisait geogebra pour en tirer les mesures.

Merci pour toutes ces explications mais les questions sont presentes comme ceci:

1-Determiner une valeur aprochees de la longueur AB (c'est dans une pyramide réguliere) pour laquelle l'aire totale de la pyramide est environ egale a 50m2
........................................................................................................................

2-Dans ce cas, quelle est aproximativement la mesure de la diagonale [bd] de la base de la pyramide?
...........................................................................................................................

3-On note O le centre du carre ABCD.Donner,dans le cas de le question 12, une valeur appprochee de la longueur OD.
..........................................................................................................................

4-En deduire une valeur approchee de la hauteur SO de la pyramide une fois celle ci construite avec S, le sommet de la pyramide.
.........................................................................................................................

5-En deduire alors une valeur approchee du volume de la pyramide SABCD.
..............................................................................................................................

Et les premiers questions a faire sur geogebra moi je l'ai fait avec des mesure au hasard mon carre.

En le deplacant j'obtient environ 4 mais pour la question 4 je ne vois pas trop comment je peux le trouver.
Pourriez vous m'expliquer pour la 4 s'il vous plait ?

oui, mais Geogebra à l'avantage énorme que ces mesures "au hasard" peuvent être modifiées dynamiquement simplement en déplaçant un point à la souris !!!

donc dans la partie tableur il faut mettre ce que doit calculer Geogebra à partir des mesures actuelles des segments réellement tracés par Geogebra
et pas des calculs que TU ferais.

et en mettant dans les cases du tableur une formule et non pas une valeur, quand on modifie la figure à la souris, la valeur affichée dans la case du tableur va se modifier automatiquement comme résultat du calcul effectué en permanence par Geogebra.

(par exemple comme j'ai dit si on voulait l'aire du carré)

ensuite la question "Déterminer une valeur approchée" consiste à déplacer à la souris le point qui "pilote" les dimensions du carré et de regarder dans la case où Geogebra calcule de façon dynamique et en permanence l'aire totale.

et de déplacer ce point jusqu'à ce qu'on lise dans la case "aire totale" la valeur 50
les m² étant remplacés par des cm² pour cause d'échelle : ta figure ne va pas faire une taille de plusieurs mètres, dans la figure les mètres sont remplacés par des cm (ou plus exactement par des "unités Geogebra") et de même les m² par des cm² les m³ par des cm³ etc


évidemment pour que tout ça marche il faut bien entendu :
- avoir construit correctement la figure qui doit donc être dynamique (on peut en modifier la taille en déplaçant juste un coin du carré et tout le reste "suit" automatiquement)
c'est réellement ça qui est demandé dans la 1ère partie

- avoir répondu correctement aux questions 10 et 11 de la première partie de sorte que Geogebra fasse ces calculs en permanence et de façon dynamique au fur et à mesure qu'on modifie la taille de la figure à la souris.

posts croisés, je répondais à la question de 22:22, pas celle de 22:31
là il faut que je fasse réellement l'exo ... pour vérifier les valeurs.
one moment please.

Juste pour être sûr, la question 1. se fait suivant les étapes suivantes :
1. on construit la figure avec un côté AB quelconque (et modifiable)
2. on remplit le tableau avec "=a" dans la cellule A2
3. on complète la cellule C2 avec ="poly1+poly2+poly3+poly4"
4. on déplace le point B pour obtenir une valeur proche de 50 dans C3
5. on lit la valeur correspondante de AB dans C1

C'est bien 5 mais pas parce que 50:5=10 et 10:2=5, ces calculs ne veulent rien dire.

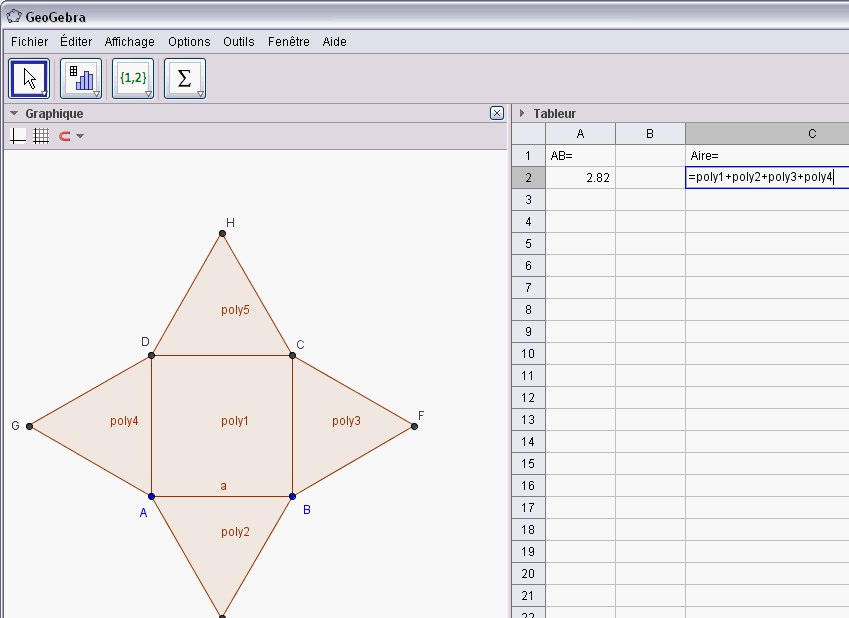
Je me suis un peu emmêlé dans les cases,
on déplace B jusqu'à obtenir une valeur proche de 50 dans C2 puis on lit la valeur correspondante dans A2

pour la question 1 de la deuxième partie j'obtiens ça :



alors on va dire 4 comme valeur approchée n'est pas entièrement faux, mais peut mieux faire !!
(beaucoup mieux, même sans atteindre ce que j'ai obtenu qui a nécessité de jouer un peu avec le zoom)

question 3 "dans le cas de le question 12," y a pas de "question 12" on va dire que la "question 12" est la question 1 de la deuxième partie...


question 4 il s'agit de montrer que la hauteur SO de la pyramide est aussi égale à OD !!

ça ne semble pas évident du tout et c'est effectivement la vraie difficulté (au sens mathématique) de l'exo.
en fait il faut, une fois repliée la pyramide, prouver que le triangle ASC est un triangle rectangle en S !!

une preuve "intuitive" est que le triangle ASC est totalement identique (mêmes mesures de côtés, le justifier) au triangle ADC
et donc il a lui aussi un angle droit en S, et surtout la hauteur SO est identique à DO

on peut aussi prouver tout ça avec des Pythagore et réciproques "en lettres"

bref, maintenant qu'on connait ce qu'est sur la figure la hauteur de la pyramide, il suffit de rajouter quelques cases dans le tableur pour avoir les réponses aux questions 4 et 5

l'aire totale de la pyramide n'est pas l'aire latérale
l'aire totale, c'est base comprise. (la somme des 5 polygones)

Bonjour merci beaucoup pour toutes ces explications mais il ne mets jamais demander de justifier  et sur ma feuille il n'y qu'une ligne pour y repondre pour chaque questions donc je pense qu'il faut juste donner le resutat mais apres quand il dise une fois celle ci construite avec S , dois-je la construire car je ne sais pas utiliser le 3D.

on n'utilise pas la 3D (de Geogebra)
on réfléchit dans sa tête comment se replie le patron d'une pyramide et on en déduit ce que j'ai dit.
au besoin on fait sur papier un dessin à main levée "de principe" de la pyramide en perspective,
juste en codant les côtés (parce qu'il y a des côtés à "coder" ne serait-ce déja que les côtés du carrés sont tous les 4 égaux)
et ce codage là c'est le "(mêmes mesures de côtés, le justifier)" de mon post précédent

pour illustrer ça par un dessin 3D (sur papier, ici certes grâce à Geogebra mais indépendamment de la figure précédente)

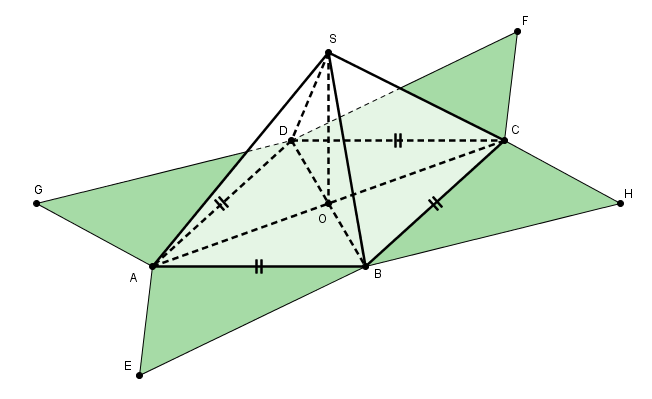
(j'ai aussi fait figurer le patron "vu en perspective" en vert)

il te reste à coder les côtés "à justifier" pour comprendre pourquoi OS = OD (relire mon post précédent)

A mathafou, j'avais oublié un triangle dans l'aire totale.
A lili33, pour le sommet S, je ne pense pas qu'on demande une figure 3D, fais une figure à main levée en perspective. Tu verras que le triangle SOD est rectangle, que son côté OS est la hauteur de la pyramide, que ses côtés OD et SD sont connus. On peut l'identifier à un triangle rectangle faisant partie du patron.

PS :

D'accord  donc je mets deux trait sur AS, SD,SB et SC mais apres comment prouver que SO=OD?

Fait apparaître, avec les points de la figure, un triangle rectangle dont l'hypoténuse est égale à AB et dont un autre côté est égale à OD.

avant tout ça il faut justifier pourquoi non seulement SA = SB = SC = SD mais aussi pourquoi, ils sont égaux à AB = BC = CD = AD !!
que toutes les arêtes de cette pyramide (les 8 arêtes) sont toutes égales !!
c'est là la clé de l'affaire

ensuite on fait comme on veut :
des Pythgaore (ou simplement imaginer que si on calculait effectivement, sans le faire ...)
ou des triangles superposables (identiques) et donc égalités de etc ...

oui d'accord mais comment prouver les 8 aretes sont tous egaux? je n'ai pas vue de propriete qui le dis.

a si j'ai une remarque dans mon cours qui dis que les aretes d'une pyramide reguliere sont de meme dimension

de quelle nature est le triangle SAB ? (= EAB)
(comment a-t-il été construit ?)

Et apres on faisant le theoreme de Pythagore dans le triangle SOD je retombe sur OD qui est environ egale 2,82.

Et apres pour le volume 1/3xV8x16 qui fait environ 15.08.

SAB est triangle equilaterale.

bein oui, donc SA = AB etc

tiens ce message était passé inaperçu (posts croisés)

D'accord mais juste pour le premier message des deux derniers dans la méthode pour calculer le volume par geogebra on ne peut pas calculer avec geogebra vue que ce ne sont pas des mesure exacte donc il faudrait plutôt calculer par écrit que l'on a trouver et quand vous dite que la mesure de OD et donnee grace a geogebra  on a pas 4 tout pile dans la mesure AB donc la aussi il serait mieux de le faire a l'écrit.

Pour la première:

La valeur approchée est 4.

Pour la deuxième:

Le triangle ABD est rectangle en A
D'apres le theoreme de Pythagore
on a, BD2=AB2+AD2
      BD2=42+42
      BD2=16+16
      BD2=32
      BD=V32
      BD= environ 5.65

Donc BD mesure environ 5.65

Pour la troisieme:

V32/2=environ 2.82
Donc OD mesure environ 2.82


Pour la quatrième:

Comme OD=SO

Alors SO=OD= environ 2.82

Pour la cinquième:

aire de la base= cxc=4x4=16

hauteur=V32/2

V=16xV32/2/3
V= environ 15.08

Ai-ce juste ?

la valeur approchée n'est pas 4 du tout .. point final (voir ma capture d'écran)


et si, cet exo consiste exclusivement à maitriser Geogebra pour lui faire mesurer, afficher et calculer des trucs
et rien d'autre.

maintenant si tu veux faire vraiment des calculs, ce n'est pas du tout ce que tu fais mais comme j'ai dit :
trouver la valeur exacte du côté qui donne l'aire totale = 50
par l'intermédiaire d'une équation (résultat suggéré par COTLOD le 28-12-14 à 20:09)
et ensuite etc (et ensuite arrondir les "valeurs exactes" pour obtenir des valeurs approchées)

mais ceci est un autre exo.

après tu en fais à ta tête, c'est toi qui vois. après tout c'est ton exo et c'est toi qui rendras ta copie hein ...

(ou le prof devait être plus clair dans la façon de poser ses questions, s'il voulait des calculs, par exemple une partie 2 de calculs théorique se terminant par "comparer avec les résultats obtenus partie 1 par Geogebra")

oui mais si la valeur aprochee n'est pas quatre c'est quoi?

Et en utiisant geogebra,
ca me donne
1- le valeur approchee est 4

2- la valeur est 6

3- la valeur do OD est 3

4- SO mesure aussi environ 3

5- le volume est 19


Mais par contre quelle est l'unite de mesure?

A non la valeur aprochee est 5 pas 4
pardon

tu n'as pas regardé ma copie d'écran ?

et tu peux toi même le faire : déplacer à la souris le point qui définit la taille du carré jusqu'à ce que la valeur affichée dans la case où on a fait calculer l'aire totale soit le plus près possible de 50

et tu verras bien...

évidemment si tu as défini ce côté bêtement par un curseur (raison pour laquelle je hais les curseurs) avec un pas de 1 ça ne le fera jamais ...

la meilleure façon de construire la figure est de fixer A (par exemple sur l'origine des coordonnées) et de placer un point B variable sur l'axe des x
puis construire tout le reste à partir de ces deux points A et B
B étant déplaçable aussi finement que l'on veut à la souris (zoomer au besoin) et pas par un pas quelconque trop imprécis
le "pas" c'est un pixel au zoom maximum c'est à dire de l'ordre de 10^-12 !!
on peut obtenir ainsi une valeur "approchée" extrêmement précise en demandant à Géogébra d'afficher ses 15 chiffres après la virgule,
mais on n'en demande pas tant, obtenir des valeurs "qui vont bien" avec deux chiffres exacts après la virgule est suffisant pour voir que ça ne fait pas 4.

ok merci mais sinon tout le reste est juste du message de 14h28? et je l'ai fais deplacee avec la souris mais je ne savais as que quand il y a deux chiffres apres le virgule on prend le chiffre d'au dessus.
Mais par contre je pense que tout doit se faire sur geogebra et don aussi la pyramide construite mais je ne sais pas comment faire.

A non ba du coup c'est
2-7
3-4
4-4
5-19

on ne te demande pas de la construire effectivement

dans l'exo on a juste le patron et rien d'autre

et "si on repliait ce patron on obtiendrait une pyramide"
c'est une action de pensée, pas un truc à faire avec ses mains (Geogebra ou pas)
dessiner effectivement une vue en perspective de la pyramide "montée" sur du papier ou tracer sur du carton le patron (en cm pas en m ) pour le découper, si ça te chante et pour aider à penser et voir comment est cette pyramide, c'est comme chacun le sent.

* et si le 3ème chiffre est 5 on arrondit le 2ème au chiffre supérieur (pas ">0")

Donc du coup ca fait:

1-La valeur est 4.28
2-La valeur est 6.06
3-La valeur est 3.03
4-La valeur est 3.03
5-La valeur est 18.6

Apres je n'est pas réussie a aller jusqu'à pile 50 donc ca ne tombera peu être pas pile sur vos résultat ce sera surement proche.

les résultats de Geogebra sont des valeurs approchées
d'abord avec la précision de placement du point, qui donne une aire seulement "à peu près 50"
ensuite parce que de toute façon ce sont des valeurs approchées (comme avec n'importe quelle calculette)
et c'est bien ces valeurs là, lues directement sur Geogebra et pas re-arrondies ni re-calculées qu'on te demande juste de recopier.

d'accord avec tes valeurs à un pouillème près
(côté = 4.28 veut réellement dire 4.275 coté < 4.285
alors "ton" 4.28, je n'ai aucune chance de le reproduire moi

en positionnant ce "4.28" à une valeur la plus proche que je peux de 4.285, j'obtiens bien tes valeurs
si on arrondit volume = 18.5445447449815 de Geogebra en 18.6 alors que ce serait plutôt 18.5 !!
tu as donc très certainement fait ton calcul de volume toi-même à partir de valeurs de côté et de hauteur déja arrondies plutôt que de faire faire ce calcul par Geogebra
(en mettant une case du tableur avec "=poly1*h/3" comme je le proposais, et qui me donne ma valeur ci-dessus)

D'accord merci mais juste une question pour être sur, d'après vous quand il dise dans la question 4 une fois celle ci reproduit avec S, Est-ce qu'il faut le reproduire par geogebra ou sur feuille car les questions sont en fait toutes a la suite et font aussi parti de dans un logiciel de géométrie dynamique.

Or si c'est sur geogebra je ne vois pas du tout comment on fait car je commence tout juste a découvrir le logiciel et je ne sais pas complètement m'en servir.

Cette question est sûrement mal exprimée. Il faut juste comprendre qu'on appelle S le sommet de la pyramide, il n'est pas question de faire de la 3D avec geogebra.

D'accord merci beaucoup pour toutes vos explication.