Inscription / Connexion Nouveau Sujet
Exercice sur triangles semblables/orthocentre
bonsoir à tous
j'ai un problème sur cet exercice, il fait partie d'une dm portant sur les triangles semblables
l'image de la figure
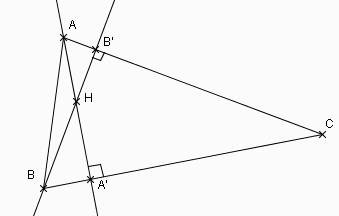
et l'énoncé
Le point H est l'orthocentre du triangle ABC
1/ Démontrer que les triangles HA'B et HB'A sont semblables.
En déduire que HA X HA' = HB X HB'
2/Quel est l'orthocentre du triangle ABC ?
En déduire que AH X AA' = AB' X AC.
merci d'avance pour votre aide, car je bloque depuis un bout de temps la
Edit Coll : image placée sur le serveur de l' 
Merci d'en faire autant la prochaine fois ! 
[lien]
Bonjour,
Pour la 1,
deux triangles sont semblables si on peut démontrer qu'ils ont deux angles égaux, ici,
les deux angles droits sont égaux HA'B et HB'A
et,HBA' et AHB' sont opposés par le sommet (donc égaux)
...
NB: faudrait mieur formuler
1 On sait que HA'B=HB'A=90°
AHB'=A'HB car opposé par le sommet
donc comme ils ont 2 angles égaux, ils sont semblables
2 Comme ils sont semblable on peut ecrire AH/HB=B'H/HA'
d'ou AH X HA'= HB X HB' (produit en croix)
Pour le reste je c pas dsl
voila
Theool
ok, merci beaucoup pour votre réponse, j'ai rédigé.
auriez vous une idée pour les suivantes ? je suppose que celle qui suit à un lien avec la première, non ??
zut, j'avais pas vu ton message theool ^^
il faut pas faire un tableau là ??
je pense faire :
On sait que les triangles sont semblables, donc leurs côtés opposés aux angles égaux sont proportionnels
cela nous donne :
HA'B HA HB' AB'
HB'A HB HA' A'B
donc, par produit en croix, on obtient HA x HA' = HB x HB'
vous en pensez quoi ?
Annuler
connectez vous