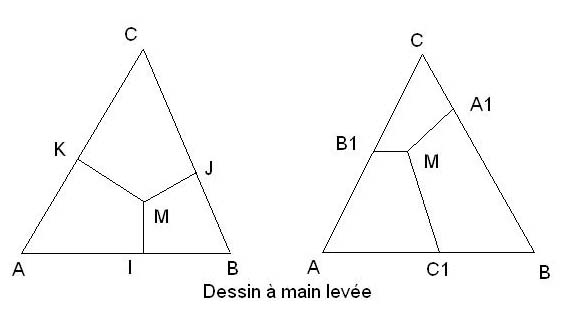
comment sont définis A1, B1 et C1 ?

Philoux

A2 ou B1 ?

Philoux

sa je ne sait pas non plus pour le montrer il est necéssaire de le savoir ?

Quelqu'un saurai résoudre cet exercice ??? svp

autrement dit

est-ce que, tout simplement :

A1M est ortho à BC

B1M est ortho à AC

C1M est ortho à AB

?

Philoux

Ca reviendrait alors à etre le même problème que le A)

Mais c'est vrai que j'ai aussi du mal à capter la question B)

je n'arrive toujour pas a montrer ces deux questions

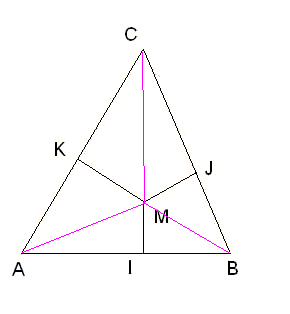
Aire(AMC) = (1/2).AC*MK
Aire(AMB) = (1/2).AB*MI
Aire(CMB) = (1/2).BC*MJ

Aire(ABC) = Aire(AMC) + Aire(AMB) + Aire(CMB)
Aire(ABC) = (1/2).(AC*MK + AB*MI + BC*MJ)

Or AC = AB + BC puisque le triangle ABC est équilatéral.
-->

Aire(ABC) = (1/2).AB.(MK + MI + MJ)

Or on a aussi Aire (ABC) = (1/2).AB.h avec h la hauteur issue de C du triangle ABC.

--> (1/2).AB.(MK + MI + MJ) = (1/2).AB.h

MK + MI + MJ = h

Et comme h est une constante pour un triangle donné, on a: MK + MI + MJ = constante.
-----

Mercii beaucoup de ton aide et de votre aidee a touss

sur cette opération comm les autres : (1/2).AB.(MK + MI + MJ) = (1/2).AB.h
Les points ( . ) remplacent koi ???

ça ne peut être que multiplié

Philoux

je doutai puisqu'a des moment il y a des *

et pour le deuxieme triangle commen fo t-il faire ?? je n'y arrive pas

Normal puisque tu n'as pas précisé ce que sont les points A1, B1 et C1 comme philoux te l'a déjà dit.

il le son sur la figure ossi ??

Jai tenter ceci , mais je suis vraiement pas sure que sa soit bon , pouriez vou maider apres ceci ? :

Aire(AMC) = (1/2).AC*MB1
Aire(AMB) = (1/2).AB*MC1
Aire(CMB) = (1/2).BC*MA1

Aire(ABC) = Aire(AMC) + Aire(AMB) + Aire(CMB)
Aire(ABC) = (1/2).(AC*MB1 + AB*MC1 + BC*MA1)


Aire(ABC) = (1/2).AB.(MB1 + MC1 + MA1)


Aire (ABC) = (1/2).AB.h avec h la hauteur issue de C du triangle ABC.

--> (1/2).AB.(MB1 + MC1 + MA1) = (1/2).AB.h

MB1 + MC1 + MA1 = h

MB1 + MC1 + MA1 = constante



Est ce bon en remplacant les donné ?

On ne peut pas t'aider, mais juste te répéter que sans savoir comment les points A1, B1 et C1 ont été placés on ne peut rien faire.

Peut-être a-t-on MC1 parallèle à BC, MB1 parallèle à AB et MA1 parallèle à AC ou bien autre chose, mais IL FAUT le savoir.

ah daccord je comprend que vou ne poiver pas maider , jvou remercie de toute votre aide en tout cas

Il faudrait surtout que tu nous DISES comment sont placés les points A1, B1 et C1, ça nous aiderait, mais toi aussi, car t'as pas l'air au courant

je ne peut pas vous dire puisque je n'ai pas plus dinformation que sa :s:s dsl

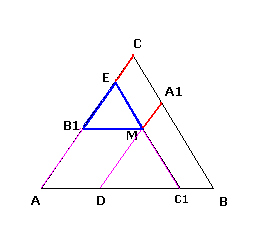
Normalement sur ma figure , tout les cote semblent etre paralelle

c'est a dire :

AC // MA1
BC // MC1
AB // MB1

Donc maintenan , est ce que ceci peut vous aider ??

Ahhhhhhhhhhhhh

mais je ne vois pas

Philoux

Si

AC // MA1
BC // MC1
AB // MB1

Alors:

MC1 = MD = AB1 (car triangle DMC1 est équilatéral)
MB1 = B1E (car triangle B1ME est équilatéral)
MA1 = EC

--> en faisant la somme membres à membres des égalités ci-dessus.

MC1 + MB1 + MA1 = AB1 + B1E + EC

MC1 + MB1 + MA1 = AC = constante (coté du triangle)
-----
Sauf distraction.