Avec une petite figure, c'est plus facile :

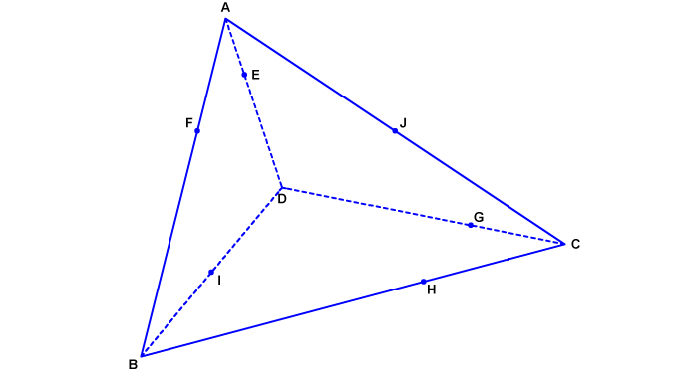
Tu peux essayer de démontrer que EFHG est un parallélogramme, pour commencer ...

Bonjour

ça c'est facile (avec des Thalès de collège, ou la même chose exprimée autrement)
la suite est plus dure (de faire ensuite intervenir IJ là dedans)

mes idées, à voir :
par exemple déja de prouver que EIHJ sont coplanaires ...



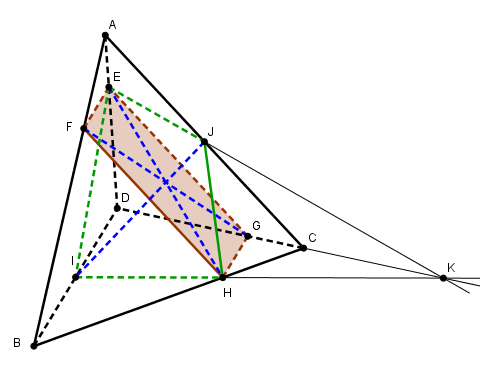
avec utilisation des barycentres tout ça devrait se faire d'un coup tout seul, ou presque, mais les barycentres sont ils vus ?
sinon ça reviendra à redémontrer des propriétés des barycentres , mais sans les barycentres (que des relations vectorielles)
(ou aussi redémontrer Ménelaüs, prouvant que CD, HI, EJ concourantes ?).

Maiss pour prouver que EFHG est un parallélogramme faut-il utiliser des égalités de vecteur?(en exprimant selon a) parcque dans cette exercice ont ne peut pas utiliser le théorème des milieux.

les milieux pour EFHG c'est rapé : il n'y a aucun milieu là dedans !!
et pour EIHJ non plus car les points E et H n'ont rien de milieux

donc de toute façon ce sera par des décompositions de vecteurs
ou choisir un repère
ou les barycentres
c'est juste une question de rédaction car c'est équivalent

C' Bon j'ai réussi en utilisant un repère en passant par les coordonnées puis les vecteurs pour trouver chacun une équation paramétrique,puis j'ai résolu un système où j'obtenais une même solution puis j'ai trouver les coordonnées du point d'intersection de ces droites qui sont donc concourants.

Bonjour,

Par exemple :
BJ coupe FH en son milieu et DJ coupe EG en son milieu.
Puis considérer le plan BDJ
Ou idem avec le plan ACI

oui, bien vu.

ce n'est vrai que une fois que l'on a démontré au préalable que FH est parallèle à AC
et exploitable uniquement après que l'on a démontré même que EFHG est un parallélogramme
donc juste pour achever la démonstration
(par des moyens élémentaires sans vecteurs ni repère)

Bonjour mathafou,

J'ai supposé la démonstration faite que  EFHG est un parallélogramme...(FH et EG parallèles à AC,
EF et GH parallèles à BD)

je m' en doute bien.
c'était pour mettre les points sur les i à destination de nicoboll77