Inscription / Connexion Nouveau Sujet
exo simple: equation plan et representation paramètrique droite
Bonjour,
Je bloque deux exercices simples, mais j'ai des difficultés
Exercice 1:
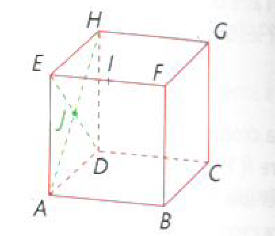
On considère le cube ABCDEFGH (voir image du cube)où I est milieu de [EF] et J le centre de la face ADHE.
On rapporte l'espace au repère (A;;
;
)
Dire si les affirmations sont vraies ou fausses:
1/L'ensemble des points M(x;y;z) tel que y=-x+41 est le plan (DBH)
2/ Le plan (AIG) est l'emble des points M (x;y;z) tels que: 2x-y-z=0
3/La droite (BJ) est orthogonale au plan (AIG).
Voici ce que j'ai fait:
j'ai trouver les coordonnées à partir du cube:
A(0;0;0)
B(1;0;0)
C(1;1;0)
D(0;1;0)
E(0;0;1)
F(1;0;1)
G(1;1;1)
H(0;1;1)
La question 1 je n'ai pas trouver
la question2, je ne suis pas sûr:
Je connais la formule de l'équation plan:
.;
=0
ax+by+cz+d=0
J'ai calculer les vecteurs AG; AI, IG, AM:
AG(1;1;1)
AI(1/2;0;1/2)
IG(1/2;1;1/2)
AM(x;y;z)
Là je ne sais plus quoi faire.
Exercice 2:
On considère la droite d intersection des deux plans d'équations cartésiennnes:
x+z=2 et x+y+z=0
Dire si les affirmations sont vraies ou fausses en justifiant votre réponses:
(A) La droite d passe par le point (o;1;2).
(B) la droite d a pour système paramètrique:
x=k+1
y=-2k, k appartient à R
z=-k+1
(C) Le vecteur (1;-2;-1) est un vecteur directeur de la droite d.
(D) La droite d est orthogonale au plan d'équation cartésienne x+y-z=2
J'ai essayé mais je n'arrive pas, pouvez-vous me donner quelques indications?
Merci de votre aide
Léa 2000
petit correction pour l'exo 1 question 1:L'ensemble des points M(x;y;z) tel que y=-x+1 est le plan (DBH)
Bonjour.
Exercice 1.
1°) Tu as deux méthodes.
a) : tu regardes si les points D, B, H vérifient y = -x + 1. Si c'est vrai alors, y = -x + 1 est bien une équation du plan (DBH).
b) Tu écris que le plan (DBH) a une équation du type ax + by + cz + d = 0. Ensuite tu remplaces successivement x, y, z par les coordonnées de D, B, H. Cela te donne un système :
a + d = 0
b + d = 0
b + c + d = 0
Tu en tires : a = -d et b = -d et c = 0.
Donc : -dx - dy + d = 0. En simplifiant par -d, on trouve effectivement y = -x + 1
2°) Tu peux procéder exactement comme pour 1°). On trouve dans les deux cas : 2x - y - z = 0.
3°) Cette dernière équation te donne un vecteur normal au plan (AIG) :
Ensuite, tu as J(1/2, 0, 1/2) et B(1, 0, 0). Cherche les coordonnées de . Si tu trouves un vecteur colinéaire à
, alors la droite (BJ) est orthogonale au plan (AIG). Sinon, c'est faux.
Je te laisse prendre contact avec tout cela. A plus RR.
J'ai essayé:
1/vecteurs:
DB(1;-1;0)
DH(0;0;1)
M (x;y;z) point quelconque.
vecteurs:
DM=aDB+bDH, a et b appartient à R
x=a*1+b*0
y=a*(-1)+b*0
z=a*0+b*1
x=a
y-1=-a
z=b
x=a
y-1=-1*x
z=b
x=a
y=-x+1
z=b
Donc vrai
2/vecteurs:
AI(1/2;0;1/2)
AG(1;1;1)
M (x;y;z) point quelconque.
vecteurs:
D
AM=aAI+bAG, a et b appartient à R
x=a*(1/2)+b*1
y=a*(0)+b*1
z=a*(1/2)+b*1
x=1/2a+b
y=b
z=1/2a+b
x=1/2a+y
y=b
z=1/2a+y
Là je bloque.
vecteurs:
AI(1/2;0;1/2)
AG(1;1;1)
M (x;y;z) point quelconque.
vecteurs:
D
AM=aAI+bAG, a et b appartient à R
x=a*(1/2)+b*1
y=a*(0)+b*1
z=a*(1)+b*1
x=1/2a+b
y=b
z=1a+b
x=1/2a+y
y=b
z=1a+y
Là je bloque pour trouver une équation plan, comment faire?
merci
Dans mon premier message, j'ai fait une erreur de frappe : c'est plutôt J(0,1/2,1/2).
Alors vecteur(BJ) : (-1,1/2,1/2) est bien colinéaire au vecteur normal au plan (AIG) : (2,-1,-1).
Donc, c'est vrai (BJ) est perpendiculaire au plan (AIG).
A plus RR.

 1/2 , 0 , 1)
1/2 , 0 , 1)

