Inscription / Connexion Nouveau Sujet
Exo triangles iso.
Bonjour, j'ai déjà posté un exo de mon D-M croyant que ca serait le seul qui me poserai problème mais en voilà un autre. Et oui, je vous demande de m'aider une fois de plus(lol)
Voila l'énoncé :
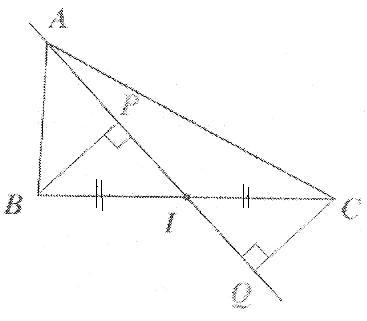
ABC est un triangle, I est le milieu de [BC], P et Q sont les pieds des perpendiculaires à (AI) issues respectivement de B et C.
Démontrer que BP = CQ en prouvant que les triangles BIP et CIQ sont isométriques.
Voila mes pistes :
-I milieu de [BC], donc BC = IC
-angles ^P et ^Q droits
Je pense qu'il faut utiliser le théorème de la droite des milieux mais je suis pas sûr, PLEASE HELP ME 
Merci d'avance
bonjour,
que dire des deux angles et
? en n'oubliant pas de justifier.
cela permet de dire que les deux triangles BIP et CIQ sont isométriques, sauf erreur.
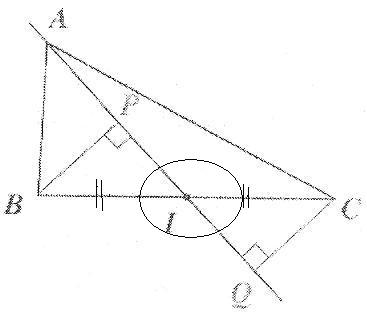
Bonjour, j'aimerais juste savoir si les angles BÎP et CÎQ sont alternes-internes ?
et si oui, comment le démontrer ?
SVP aidez-moi, c'est pour un D-M à rendre demain.
Merci d'avance
*** message déplacé ***
Bonjour,
Des angles alternes-internes sont déterminés par deux parallèles et une séquente, ce n'est pas le cas ici. En revanche, ils sont tout de même égaux car déterminés par l'intersction des droites BIC et AIQ
*** message déplacé ***
non, les angle sont opposés par le sommet (même sommet et portés par les mêmes côtés). Ce qui compte c'est que ces angles sont égaux.
Pour conclure : les triangles sont isométriques.





