Inscription / Connexion Nouveau Sujet
Figure: Equation
Bonjour, j'ai un exercice de maths que je ne comprends pas...
Pouvez-vous m'aider s'il vous plait? 
Voilà une image de la figure et de son énoncé...
Merci, Chaimathematique 
Bonsoir.
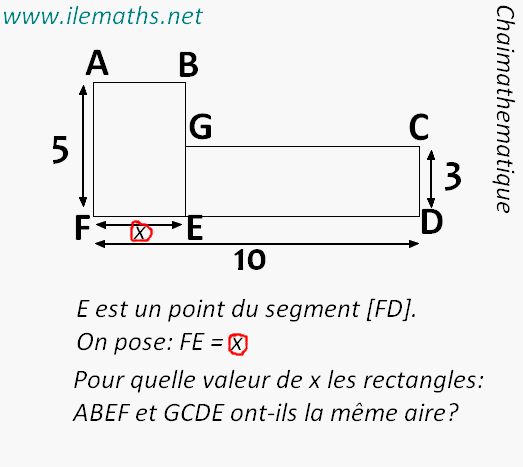
L'aire de ABEF est : 5*x = 5x
L'aire de GCDE est : 3*(10-x) = 30 - 3x
Il suffit donc de résoudre l'équation suivante :
5x = 30 - 3x
C'est dans tes cordes, je pense.
bonsoir
tu connais la formule permettant de calculer l'aire d'un rectangle ?
écris l'aire du rectangle AFEB et celle de GCDE, puis l'égalité de ces deux aires
Pouvez-vous me corriger si j'ai des fautes...
5x = 30 - 3x
5x + 3x = 30
8x = 30
Ensuite j'ai un trou... Je ne sais pas si je dois faire:
8x/8 et on obtiens x=30 Mais la longueur du segment [FD] est égale à 10
J'ai donc fait une erreur dans une étape de la résolution de l'équation :s
bonsoir
tu connais la formule permettant de calculer l'aire d'un rectangle ?
écris l'aire du rectangle AFEB et celle de GCDE, puis l'égalité de ces deux aires
Oui c'est Longueur*largeur, L*l..
L'aire de ABEF est 5*x = 5x
L'aire de GCDE est 3*(10-x) = 30 - 3x
...
L'égalité: 5x = 30 - 3x
et oui c'est bien ça, Dommage que Erainel t'aie donné directement la réponse sans te laisser chercher un peu 
Il faut diviser les 2 côtés par 8:
8x/8=30/8
J'obtiens donc: x = 3,75
10-3,75 = 6,25
Aire du rectangle ABEF: 5*3,75 = 18,75
Aire du rectangle GCDE: 3*6,25 = 18,75
Phrase de conclusion: Il faut que la valeur de x soit 3,75 pour que les rectangles ABEF et GCDE aient la même aire.
Merci pour tout! Bonne soirée

Chaimathematique
et oui c'est bien ça, Dommage que Erainel t'aie donné directement la réponse sans te laisser chercher un peu
J'ai fait la vérification haha :p



