Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Limites de fonctionsTopics traitant de Limites de fonctions [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Fonction,asymptotes et suite

Posté par
Kylinn 06-10-08 à 01:21

Bonjour j'ai un exercice à remettre pour mardi 7et je n'ai pas compris comment faire pour répondre à certaines questions.

f est la fonction définie sur R-{-1;0} par: f(x)=2x²+2x-1/x²+x
C est sa courbe représentative dans un repère orthonormal (unité:2cm)

1.vérifier que,pour tout réel x différent de 0 et de -1:
f(x)=2-(1/x)+(1/x+1)
voici ma réponse:
f(x)=2-(1/x)+(1/x+1)=(2x(x+1)-(x+1)+x)/x(x+1)=2x²+2x-1/x²+x

2.Etudier les limites de f en moins l'infini,plus l'infini,-1 et 0
3.en déduire les équations des asymptotes à C
je sais pas comment répondre à ces deux questions

4. D est la droite d'équation y=2.Etudier la position de C par rapport à D.
Voici ma réponse:
(2x²+2x-1)/(x²+x) - (2/1)
=[(2x²+2x-1)-(2x²+2x]/(x²+x)
=(2x²+2x-1-2x²-2x)/(x²+x)
=-1/(x²+x)
= -1 / x(x+1)
_Quand x est grand (+ l'infini) x(x+1) est positif et -1 / x(x+1) est négatif,donc f(x) - 2 < 0 <=> f(x) < 2
Conclusion:la courbe C est en dessous de la droite D
_quand x est  petit(- l'infini), x(x+1) est positif, et -1 / x(x+1) est négatif,donc f(x) - 2 < 0 <=> f(x) < 2
Conclusion:la courbe C est en dessous de la droite D

5.calculer f'(x);en déduire le sens de variation de f.Dresser le tableau de variation de f.
Voici ma réponse:
f(x)=2x²+2x-1/x²+x
f'(x)=(2*2x+2-0)/(2x+1)=4x+2/2x+1
Donc f'(x) est supérieur à zéro pour tout x appartenant à R.
J'sais pas comment faire le tableau de variation,quels valeurs j'dois mettre?

6. x est un réel distinct de -1/2 et 1/2;
A)vérifier que -1/2-x et -1/2+x sont différents de 0 et 1.
b)A et B sont 2 points de C,d'abscisses respectives -1/2-x et -1/2+x
Comparer leurs coordonnées.Interpréter graphiquement ce résultat.

7.a)Calculer les coordonnées des points d'intersection de C avec l'axe des abscisses.
b)Tracer la courbe C et ses asymptotes.

8.u est la suite définie pour tout entier nsupérieur ou égal à 1 par
u n=2-f(n)
a)représenter sur le graphique u1,u2 et u3 après avoir donné une interprétation graphique de ces réels
b)Calculer S n=u1+u2+...+u n en utilisant la question 1
c)Calculer lim S n
            n-) + l'infini
e la question 6 à 8 j'ai rien compris j'aimerais une aide s'il vous plaît merci d'avance.

Posté par
Kylinn Exercice Fonction,asymptotes et suite 06-10-08 à 01:49

Quelqu'un peut m'aider s'il vous plaît

*** message déplacé ***

Posté par
cailloux Correcteurre : Fonction,asymptotes et suite 06-10-08 à 14:38

Bonjour,

2)3) \lim_{x\to \pm\infty}f(x)=\lim_{x\to\pm\infty}\frac{2x^2}{x^2}=2

et la droite horizontale d' équation y=2 est asymptote à C en -\infty et +\infty

\lim_{x\to -1}(2x^2+2x-1)=-1

\lim_{\stackrel{<}{x\to -1}}x^2+x=0^+ donc \lim_{\stackrel{<}{x\to -1}}f(x)=-\infty

\lim_{\stackrel{>}{x\to -1}}x^2+x=0^- donc \lim_{\stackrel{<}{x\to -1}}f(x)=+\infty

La droite verticale d' équation x=-1 est asymptote à C

\lim_{x\to 0}(2x^2+2x-1)=-1

\lim_{\stackrel{<}{x\to 0}}x^2+x=0^- donc \lim_{\stackrel{<}{x\to 0}}f(x)=+\infty

\lim_{\stackrel{>}{x\to 0}}x^2+x=0^+ donc \lim_{\stackrel{<}{x\to 0}}f(x)=-\infty

La droite verticale d' équation x=0 est asymptote à C

4) f(x)-2=-\frac{1}{x}+\frac{1}{x+1}=-\frac{1}{x(x+1)}

Sur ]-\infty,-1[\cup]0,+\infty[, f(x)-2<0 et C est au dessous de d d' équation y=2

Sur ]-1,0[, f(x)-2>0 et C est au dessus de d d' équation y=2

5) f'(x)=\frac{1}{x^2}-\frac{1}{(x+1)^2}=\frac{2x+1}{x^2(x+1)^2}

f'(x)=0 pour x=-\frac{1}{2}

Sur ]-\infty,-1[\cup ]-1,-\frac{1}{2}[, f'(x)\leq 0 et f est décroissante.

Sur [-\frac{1}{2},0[\cup ]0,+\infty[, tex]f'(x)\geq 0[/tex] et f est croissante.

6)a) Si x\not=-\frac{1}{2}, -\frac{1}{2}-x\not=0 et -\frac{1}{2}+x\not=-1

Si x\not=\frac{1}{2}, -\frac{1}{2}-x\not=-1 et -\frac{1}{2}+x\not=0

b) f\left(-\frac{1}{2}-x\right)=\frac{2(-\frac{1}{2}-x)^2+2(-\frac{1}{2}-x)-1}{2(-\frac{1}{2}-x)^2+2(-\frac{1}{2}-x)}=\frac{4x^2-3}{4x^2-1}

On trouve de même f\left(-\frac{1}{2}+x\right)=\frac{4x^2-3}{4x^2-1}

On a donc f\left(-\frac{1}{2}-x\right)=f\left(-\frac{1}{2}+x\right)

La droite verticale d' équation x=-\frac{1}{2} est axe de symétrie de C

7)a) f(x)=0\Longleftrightarrow 2x^2+2x-1=0

x_1=\frac{-1-\sqrt{3}}{2} et x_2=\frac{-1+\sqrt{3}}{2}

sont les abscisses des points d' intersection de C avec x'Ox

b)
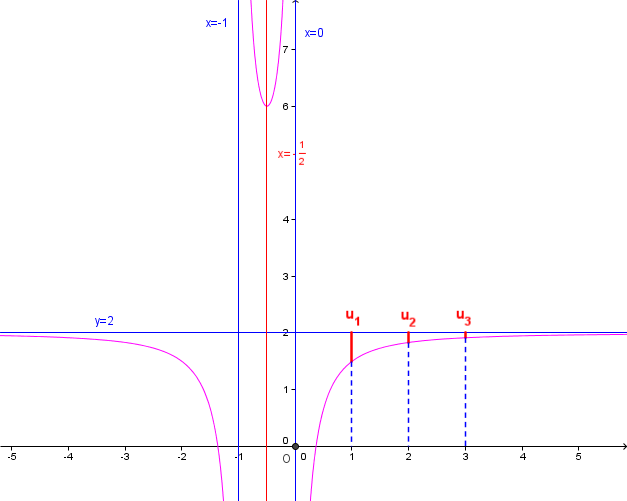
Fonction,asymptotes et suite

8)a) (voir graphique)

b) S_n=u_1+u_2+\cdots+u_n=(2-f(1))+(2-f(2))+\cdots+(2-f(n))

S_n=\left(\frac{1}{1}-\frac{1}{2}\right)+\left(\frac{1}{2}-\frac{1}{3}\right)+\cdots+\left(\frac{1}{n}-\frac{1}{n+1}\right)

S_n=1-\frac{1}{n+1}=\frac{n}{n+1}

c) \lim_{n\to +\infty}S_n=1

Posté par
Kylinnre : Fonction,asymptotes et suite 06-10-08 à 18:43

Bonsoir
Merci beaucoup
bye.

Posté par
Muffinsre : Fonction,asymptotes et suite 06-04-11 à 16:38

Bonjour! J'ai le même exercice a faire pour demain!

J'aimerai avoir quelques explications car il y a des réponses que je ne comprend pas.

La question 6 :

x est un réel distinct de -1/2 et 1/2;
A)vérifier que -1/2-x et -1/2+x sont différents de 0 et 1.
b)A et B sont 2 points de C,d'abscisses respectives -1/2-x et -1/2+x
Comparer leurs coordonnées.Interpréter graphiquement ce résultat.

a) J'aimerai que vous m'expliquiez votre réponse car je ne comprend pas ce qui permet de dire ça ? Enfin comment on le sait!
b) J'aimerai savoir pourquoi vous multipliez le dénominateur par 2 ? ( à la base le dénominateur vaut x²+x et d'après ce que je comprend de votre réponse il vaut 2x²+2x )

En espérant que vous pourrez m'éclaircir  !

Merci d'avance !

Posté par
nsophiere : Fonction,asymptotes et suite 26-10-11 à 01:21

Bonjour, j'ai également un problème sur cette exercice..
Mais je bloque sur les questions depuis la question 5

Je pose les questions qui me bloque, en espèrent que vous pourriez m'aidez..

5.Calculer f '(x);en déduire le sens de variation de f. Dresser le tableau de variation de f.
( j'ai regarder les réponses qui sont au dessus, mais je ne comprend pas comment on peut arriver à ce résultat, je ne trouve pas les mêmes résultats )

6. x est un réel distinct de -1/2 et 1/2;
a) Vérifier que -1/2-x et -1/2+x sont différents de 0 et 1.
b) Comparez les images de f (-1/2 -x) et f (-1/2 +x)

7.a) Calculer les coordonnées des points d'intersection de C avec l'axe des abscisses.
b)Tracer la courbe C et ses asymptotes.

S'il vous plait ! se serait vraiment gentil de votre part de m'aidez..

Posté par
nsophiere : Fonction,asymptotes et suite 26-10-11 à 14:32

Personne pour m'aider ?

Posté par
cailloux Correcteurre : Fonction,asymptotes et suite 27-10-11 à 19:04

Bonjour,

Mais cette partie de l' exercice a aussi été résolue à 14h38

Posté par
nsophiere : Fonction,asymptotes et suite 30-10-11 à 10:17

Oui je l'ai bien vu, mais lorsque je ne comprend pas comment on arrive au résultat posé.. je bloque.
cailloux, comment vous êtes arrivé à trouver f'(x)={1}/{x^2}-{1}/{(x+1)^2}={2x+1}/{x^2(x+1)^2}, pour la question 5 ?

Posté par
nsophiere : Fonction,asymptotes et suite 30-10-11 à 12:21

pour la question 5

Citation :
5.Calculer f '(x);en déduire le sens de variation de f. Dresser le tableau de variation de f.

Je ne trouve pas la même choses..
f(x)=2x²+2x-1/x²+x
f'(x) = 4x + 2 / 2x + 1

donc f'(x) > 0 pour tout x appartenant à R

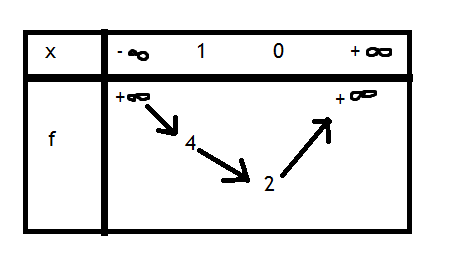
Fonction,asymptotes et suite

Posté par
cailloux Correcteurre : Fonction,asymptotes et suite 30-10-11 à 14:39

5) f(x)=2-\dfrac{1}{x}+\dfrac{1}{x+1} (voir question 1))

Donc f'(x)=\dfrac{1}{x^2}-\dfrac{1}{(x+1)^2}

f'(x)=\dfrac{(x+1)^2-x^2}{x^2(x+1)^2}

f'(x)=\dfrac{2x+1}{x^2(x+1)^2}

Bref, ta dérivée est fausse...

Posté par
nsophiere : Fonction,asymptotes et suite 30-10-11 à 18:38

AH D'accord..
c'est bizzar, je n'ai jamais cela en cour..
mais pourquoi les x devient x² ?
quand elle se dérive ne devrait elle pas se transformer et obtenir : 1 ?

Posté par
nsophiere : Fonction,asymptotes et suite 30-10-11 à 18:39

Je n'ai jamais vu cela en cour *

Posté par
cailloux Correcteurre : Fonction,asymptotes et suite 31-10-11 à 00:40

Eh bien, c' est une lacune...à combler bien sûr...

Posté par
nsophiere : Fonction,asymptotes et suite 31-10-11 à 20:46

Mais comment passe ton de
f(x)=2-(1/x)+(1/x+1) a
f'(x) = 1/x² - 1/(x+1)² ?

Posté par
cailloux Correcteurre : Fonction,asymptotes et suite 31-10-11 à 22:11

La dérivée de la fonction x\mapsto \dfrac{1}{x} est la fonction x\mapsto -\dfrac{1}{x^2}

La dérivée de la fonction x\mapsto \dfrac{1}{u(x)} est la fonction x\mapsto -\dfrac{u'(x)}{[u(x)]^2}

Tout ceci figure dans le cours de 1 ère.

Posté par
nsophiere : Fonction,asymptotes et suite 31-10-11 à 22:42

ah oui je comprend !

Mais sur ce que vous avez écrit précédemment :


Citation :
Sur ]- , -1 [ U ] -1 ; -1/2[ f'(x) 0 et f est décroissante.

Sur [-1/2 ; 0[ U ] 0 ; +[ f'(x)0 et f est croissante.


Lorsque je le met en tableau, je relève un problème..
Les chiffres trouver ne correspondent pas au signe..
Est ce un problème venant de vous ou bien de mes calcules ( résultat mise en rouge) ? :s

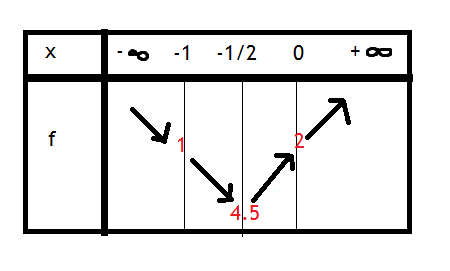
Fonction,asymptotes et suite

Posté par
cailloux Correcteurre : Fonction,asymptotes et suite 31-10-11 à 22:54

Mais en -1 et en 0, la fonction n' est pas définie (le dénominateur s' annulle) et tu dois avoir des double barres dans ton tableau de variation avec les limites calculées aux bornes de l' ensemble de définition...

De plus f\left(-\dfrac{1}{2}\right)=6 et non pas 4.5

Posté par
nsophiere : Fonction,asymptotes et suite 31-10-11 à 23:13

mais le sens des flèches est juste ? car j'ai l'impression que non...
sa ne devrait pas être l'inverse ?
Je pris en compte ce que vous m'avez dit, et donc je trouve cela comme tableau de variation de f.

est ce juste ?

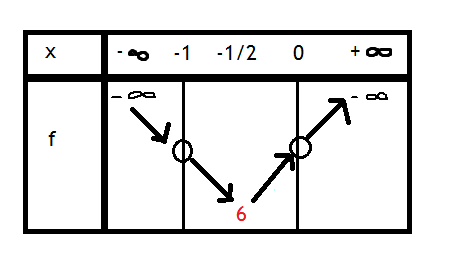
Fonction,asymptotes et suite

Posté par
nsophiere : Fonction,asymptotes et suite 31-10-11 à 23:17

Comment trouvez vous f ( -1/2) = 6 ?
Car je refait le calcule :
f(x)=2-(1/x)+(1/x+1)
comme -1.2 = -0.5 on va se facilité a prendre se chiffre
f(-0.5)=2-(1/-0.5)+(1/-0.5+1) = 4.5 :s

Posté par
cailloux Correcteurre : Fonction,asymptotes et suite 31-10-11 à 23:29

Citation :
f(-0.5)=2-1/(-0.5)+1/(-0.5+1)


oui

Citation :
= 4.5


non, ça fait 6...

Posté par
nsophiere : Fonction,asymptotes et suite 31-10-11 à 23:34

ah oui c'est vrais.. j'ai du mal taper dans ma calculatrice..
Pourriez vous voir mon post à 23h13 ?

Posté par
cailloux Correcteurre : Fonction,asymptotes et suite 31-10-11 à 23:46

Ca ne va pas:

En -1 et 0, f n' est pas définie

Posté par
nsophiere : Fonction,asymptotes et suite 01-11-11 à 08:33

f n'est pas définie.. Oui car c'est une valeur interdite non ?
mais donc que dois je mettre ?
Alors l'intervalle dans le tableau as ce que j'ai compris, est -1 et 0
et nous avons aussi -1/5 qui se pose au milieu des deux. Ce n'est pas ça ?

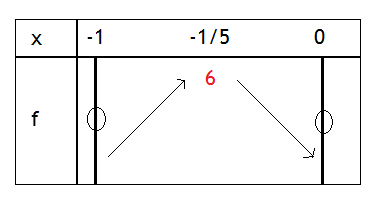
Fonction,asymptotes et suite

Posté par
cailloux Correcteurre : Fonction,asymptotes et suite 01-11-11 à 11:57

Non, toujours pas.

De toute manière les variations de f et le graphe de cette fonction sont donnés au dessus à 14h38: il suffit de lire; le tableau de variation en découle.

Posté par
nsophiere : Fonction,asymptotes et suite 01-11-11 à 13:17

Oui j'ai bien lu :

Citation :

Sur ]- , -1 [ U ] -1 ; -1/2[ f'(x) 0 et f est décroissante.

Sur [-1/2 ; 0[ U ] 0 ; +[ f'(x)0 et f est croissante.


C'est bien cela n'est ce pas ?

mais lorsque je le reporte en tableau de variation, (je vais me répétrt) je relève un problème
voir poste à 22h42  

Posté par
cailloux Correcteurre : Fonction,asymptotes et suite 01-11-11 à 20:20

Oui, c' est bien cela et il n' y a aucun problème:

Sur ]-\infty,-1[, f est décroissante de 2 à -\infty.

Sur ]-1,-\frac{1}{2}], f est décroissante de +\infty à 6.

Sur [-\frac{1}{2},0[, f est croissante de 6 à +\infty.

Sur ]0,+\infty[, f est croissante de -\infty à 2.

Posté par
nsophiere : Fonction,asymptotes et suite 01-11-11 à 20:41

ah oui je vois mieux ! merci beaucoup !

Posté par
cailloux Correcteurre : Fonction,asymptotes et suite 01-11-11 à 20:58

De rien nsophie


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1750 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !