Inscription / Connexion Nouveau Sujet
fonction cosinus,sinus et tangente,un probleme a resoudre
bonjour,je suis embeté sur un exercice,y aurai t il quelqu un qui pourrait voler a mon secours,merci d avance a celui ou celle qui pourra me repondre.
les angles utilises sont non orientes mais leur mesure etant comprise entre 0 et pi,on pourra les considerer comme des angles orientes de sens positif.on considere un triangleABC avec l angle A aigu,on note a=BC,b=AC et c=AB
1)en utilisant le projete orthogonal de C sur le cote AB montrer que l aire du triangle ABC est S=1/2bc sin A
2°)on suppose que l angle A est cette fois ci obtus,montrer que la formule trouvee en 1 reste encore valable
3)sans faire de calculs donner deux autres formules analogues pour S.
je vous remercie.
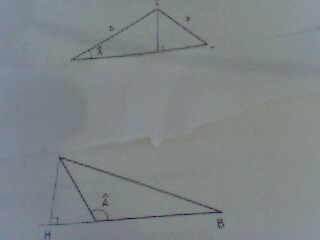
Dans le 1er cas (figure 1): S=(1/2)*Base*Hauteur=(1/2)*AB*CH
or comme AHC est un triangle rectangle en H alors sin(A)=CH/AC donc CH=AC*sin(A)
d'où S=(1/2)AC*AB*sin(A)=(1/2)bc*sin(A)
Pour la deuxième figure c'est la même chose il faut juste remarquer que: sin(x)=sin( -x)
-x)
Bonjour,
1) soit H le projet orthogonal de C sur (AB), d'après la formule de l'aire d'un triangle,
S = 1/2 * base * hauteur = 1/2 * AB * CH.
Or AB = c et (en utilisant les formules de trigonométrie dans le triangle rectangle AHC, on a sin(A) = CH/b
Donc CH = b * sin(A)
Conclusion : S= 1/2 * c * b * sin(A) = 1/2 bc sin A
2) on a toujours S = 1/2 * base * hauteur = 1/2 * AB * CH.
Or AB = c et (en utilisant les formules de trigonométrie dans le triangle rectangle AHC, on a cos(Pi-A) = CH/b.
Or on sait que cos(Pi-A)=sin(A)
On obtient alors la meme formule
3) par analogie, on a S=1/2 bc sin A = 1/2 ab sin C = 1/2 ac sin B
ManueReva
Or on sait que cos(A) = co
Pardon oui, c'est sin(Pi-A)=sin(A) et pas cos(Pi-A)=sin(A)
Mea culpa
(désolée aussi pour la fin de mon message, mauvais copié collé)
j'vais me recoucher ...


