Inscription / Connexion Nouveau Sujet
Fonction expo et suites
Bonjour,
Je rencontre quelques difficultés sur l'exercice suivant, dont voici l'énoncé:
Soit la fonction: f(x) = e(x)- x définie sur R+.
1. Etudier les variations de f.
2. Soit n un entier naturel non nul. Monter que f(x)=n admet une solution unique notée an.
3.a. Donner la valeur exacte de a1.
3.B. EN DETAILLANT, Donner une valeur approchée de a2 et a3 à 10-2 près.
4. Monter que la suite an est croissante.
5.a. La suite an peut-elle être majorée?
5.b. En déduire la limite de la suite an?
6. Déterminer la limite de e(an)/n2 quand n tend vers +
?
Voici mes réponses partielles:
1. La fonction est croissante sur [0; +[.
Sa limite en + est +
Elle croit de 1 à +
Sa dérivée est e(x)-1
Bref pas de soucis sur cette question.
2.J'ai montré que f est continue et strictement monotone sur R+.
Donc d'après le corolaire du TVI, l'équation admet 1 solution unique sur l'intervalle.
3.a. D'après le tableau de variations, on trouve a1 = 0.
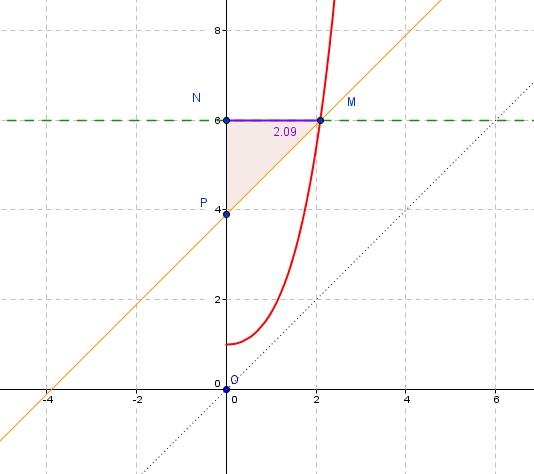
3.b. Graphiquement je trouve: 1,14 < a2 < 1.16 et 1.50 < a3 < 1.52
Là je ne sais pas si je peux faire mieux qu'une solution graphique compte-tenu qu'il est demandé de détaillé.
4. f est croissante sur R+.
donc f(1)<f(2)<...<f(n)
donc a1<a2<...<an
donc an est croissante.
Je ne suis pas certain de cette réponse.
Pour le reste, je suis bloqué.
Merci d'avance pour votre aide.
Bonjour,
3.a. D'après le tableau de variations, on trouve a1 = 0
Ce ne peut être cela, regarde bien.
Exact.
Je trouve donc a2 = 1,15 et a3 = 1,51.
Mais quelle est la méthode? C'est bien graphique? Y a t-il un autre moyen?
Et pour l'instant moi non plus 
J'ai quelques idées en tête, mais pour l'instant je n'y suis pas totalement.
Grrrrrrrr ...............
Nom de nom, je tourne autour mais je ne trouve pas la solution théorique.
Je pensais, mais non, ça ne colle pas !
Bonjour,
J'essaie en vain d'avoir de l'aide pour un post que je remonte régulièrement.
Quelqu'un m'a répondu au début pour s'avouer finalement vaincu.
Depuis je n'obtiens pas d'aide.
Voici mon post:
Fonction expo et suites
Je ne cherche pas à faire du double post mais le fait qu'il y ait déjà eu plusieurs échanges sur mon post, personne de s'y intéresse plus.
Merci de votre compréhension
J'ai été demandé de l'aide à quelqu'un, il te reste à patienter un peu.
Sache que j'ai continué de chercher de mon côté, et je ne pense pas que la solution théorique relève du niveau Terminale (mais je ne suis pas non plus à l'abri d'une faiblesse qui me fait passer à côté du "truc")
Désolé, mais je pensais que tu avais abandonné.
C'est vrai que plus personne ne s'intéresse aux posts en cours avec déjà des réponses.
Il n'y a pas de soucis, je patiente. 
Encore merci.
on ne peut pas trouver la solution exacte de ea2-a2 = 2 oui bien ea3-a3 = 3
on ne peut trouver que des valeurs approchées (c'est ce que l'énoncé demande d'ailleurs).
Pour trouver une solution approchée, on peut pas exemple procéder par dichotomies successives (en repérant d'abord un intervalle où se situe la solution, en testant le point milieu et en retenant les deux bornes pour lesquelles la fonction continue à changer de signe puis en recommençant, etc.. jusqu'à que la précision soit bonne)
a2 ~ 1.14919
a3 ~ 1.50524
Bonjour Glapion,
Merci pour ton intervention.
Donc ma réponse est bonne pour cette question.
Peux-tu m'aider pour la suite ?
suite croissante ?
tu as montré que la fonction f(x) = ex-x était croissante
l'intersection de cette courbe avec la droite horizontale y = n aura donc forcement une abscisse croissante avec n.
Ensuite on a ean-an = n
le membre de droite tend vers l'infini avec n donc le membre de gauche aussi. le seul moyen qu'il tende vers l'infini est que ean tende vers l'infini et le seul moyen qu'une exponentielle a de tendre vers l'infini est que an tende vers l'infini.
Glapion, Merci d'être venu me donner un coup de main 
(Peut-être est-il temps que l'année se termine pour moi ...)
Dans ce cas je ne vois pas à quoi sert la dernière question de mon problème et je ne vois d'ailleurs pas comment la résoudre.
Je tombe sur une forme indéterminée /
il faut prendre des initiatives et chercher un peu.
on sait que ean-an = n, ça donne furieusement envie de diviser par n² puisque l'on nous demande ce que devient ean/n² à l'infini.
ean/n²-an/n² = 1/n
Là on se dit, on va poser L = la limite de ean/n² et regarder un peu ce que devient cette égalité quand n devient grand.
quand n est assez grand L ~ ean/n² ean ~ Ln² an ~ ln L + 2 ln n et donc an/n² tend vers 0
donc si on passe ean/n²-an/n² = 1/n à la limite, tous les termes tendent vers 0 et donc L = 0
C'est le principe. il faut peut-être y mettre un peu plus de rigueur car faire des opérations sur des équivalents n'est pas toujours autorisé mais au moins on a trouvé la limite.
Merci
Pas si évident que cela pour moi de mener ce raisonnement.
Mais j'ai compris ce que tu m'as fait.
Merci beaucoup.
Merci à tous les deux.
Au passage, je connais la fonction ln mais nous ne l'avons pas encore vu en classe.
D'où mon agacement.
Je sais que j'ai un prof qui pousse parfois...
Bonne journée et bon réveillon!!!
Annuler
connectez vous