On trace la courbe, et on voit que c'est 4. Tu peux appeler ça une conjecture si tu veux...

Bonjour !

Effectivement, la correction est un peu trop rapide pour le coup ^^'

Y a-t-il un dessin avec ?

Sinon, il faut le résoudre analytiquement :

F(x) est une fonction polynôme de troisième degré, elle possède donc au moins un point de symétrie.
La fonction n'étant pas une fonction constante, elle ne possède qu'un seul point de symétrie.

Il existe donc un point M(a,b) de f(x) tel que pour tout x réel :

f(x+a)-b=-(f(-x+a)-b)

En effet, f(x+a)-b permet de « déplacer » notre origine au point M, et une fonction polynôme g(x) de troisième degré centré au point (0,0) est telle que g(x)=-g(-x).

f(x+a)-b=(x+a)^3-12.(x+a)²+7-b
f(x+a)-b =x^3+3.x².a+3.x.a²+a^3-12.(x²+a²+2.a.x)+7-b
f(x+a)-b =x^3+(3.a-12).x²+(3.a²-24.a).x+a^3-12.a²+7-b

f(-x+a)-b=(-x+a)^3-12.(-x+a)²+7-b
f(-x-a)-b =-x^3+3.x².a-3.x.a²+a^3-12.(x²+a²-2.a.x)+7-b
f(-x-a)-b =-x^3-(12-3.a).x²-(3.a²-24.a).x+a^3-12.a²+7-b
f(-x-a)-b=-(x^3+(12-3.a).x²+(3.a²-24.a).x-a^3+12.a²-7+b)

Dire que, pour tout x réel, f(x+a)-b=-(f(-x+a)-b) revient à dire que, d'après la règle de l'égalité des polynômes (Je me souviens plus du nom ^^'):

x^3= x^3
3.a-12= 12-3.a
3.a²-24.a=3.a²-24.a
a^3-12.a²+7-b=- a^3+12.a²-7+b


D'où:
3a=12
2.a^3-24.a²+14= 2.b

a=4
b=a^3-12.a²+7

a=4
b=64-12*16+7=-121

Les coordonnées de son centre de symmetries sont: M(4,-121)


Voilou

Salut salut !

Soit un dessin est fourni sur lequel est indiqué que 4 est l'abscisse du centre de symétrie, soit il faut le résoudre analytiquement.

Croire ce que l'on voit sur sa calculatrice peut être une grande source d'erreur.

Si l'abscisse du centre de symétrie était 4.01, par exemple, la calculatrice semblera t'indiquer que 4 est solution, bref en faisant soi-même le dessin on sera poussé à l'erreur.

De plus, marquer sur ta copie : « D'après ma calculatrice, 4 semble être solution » sera sans doute peu apprécié par un professeur de mathématique ^^'

La calculatrice nous aide à trouver une approximation du résultat, mais pour en être certain, la lecture graphique ne suffit pas.

Si c'était 4.01, le calcul du premier message ne fonctionnerait pas, car le résultat dépendrait alors de h.

P.S. : La correction a éta mal recopiée, c'est évidemment (f(4+h)+f(4-h))/2 = -121.

Merci à tous pour votre aide

Oui il y avait un graphique mais utiliser la conjecture pour résoudre l'exercice m'a surpris.

"En effet, f(x+a)-b permet de « déplacer » notre origine au point M, et une fonction polynôme g(x) de troisième degré centré au point (0,0) est telle que g(x)=-g(-x). "

On fait donc un changement de repère ?
Pourquoi c'est -b et non +b ?


x^3= x^3 
3.a-12= 12-3.a
3.a²-24.a=3.a²-24.a
a^3-12.a²+7-b=- a^3+12.a²-7+b 
D'où:
 3a=12 
2.a^3-24.a²+14= 2.b

Je ne comprends pas ce que vous avez fait ici

Je viens de comprendre ton raisonnement.

Effectivement si la question est comment voir que la réponse est 4, alors oui, graphiquement cela peut parfaitement confirmer le résultat.

J'ai juste compris la question différemment : « Ce que je ne comprends c'est comment on trouve le "4", on part d'une conjecture ? »

Pour moi ino cherchait à trouver ce résultat, dans le sens avoir la démarche pour arriver à ce résultat… (D'une part parce que la question de conjecture était posée et d'autre part parce que je pensais que la correction était annexe, qu'ino ne sachant pas comment résoudre ce problème ai regardé la solution et ne la comprenant pas l'ai posé).

Enfin bon, quoi qu'ai voulu savoir ino : la démonstration ou la vérification, j'imagine que l'on a pu y répondre, enfin j'espère ^^'...

Donc on utilise la lecture graphique ?

Et imaginons comme vous l'avez dit plus haut que la réponse soit 4.01 ?

Salut à tous,

Si la question est : "comment trouver ce 4", il suffit de chercher le point d'inflexion de la courbe, ie le point où la dérivée seconde s'annule.

Si f(x)=x³-12x²+7, alors f'(x)=3x²-24x et f''(x)=6x-24

Donc f''(x)=0 6x-24=0 x=4

et f(4)=-121

D'où les coordonnées du centre de symétrie.

Quelle est cette règle ?
J'en ai jamais entendu parler

Ah, je viens de voir que tu avais reposté.

Alors effectivement j'ai été un peu trop flou à ce moment-là.

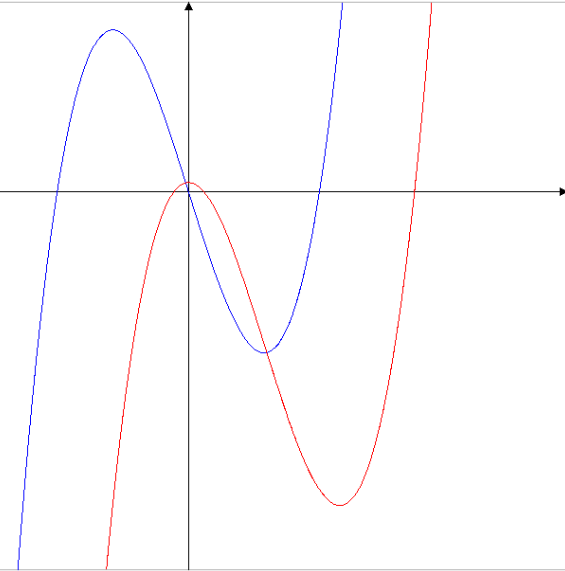
Le but de ce passage est de « déplacer » la fonction de façon à positionner son centre au point  (0,0), avec un dessin ce sera plus explicite :

"Voir l'image liée"

La courbe rouge est la courbe représentative de la fonction f(x) et la courbe bleue est celle une fois « déplacée ».

Dans quel but :

Cela se voit facilement graphiquement : la fonction est asymétrique :
g(x)=-g(-x)

Comment faire :
Pour déplacer une courbe vers la gauche, on rajoute un réel a : f(x+a)
Pour déplacer une courbe vers le haut, on enlève un réel b : f(x)-b

Dans notre cas de figure, les coordonnées de notre centre de symétrie sont les valeurs a et b, du coup pour pouvoir déplacer ce centre à l'origine il faut donc rajouter le a et le b, g(x)=f(x+a)-b

Et on sait que g(x)=-g(-x), d'où la formule f(x+a)-b=-(f(-x+a)-b) et ce qui en découle

Et on a bien après : pour tour h

(ou bien si tu préfères )

bonjour

si I(a;b) est un centre de symétrie de Cf et si f est deux fois dérivable alors Cf change de concavité en a. donc f"(a)=0  cad la dérivée seconde s'annule en a.

dans le cas de f(x)=x^3-12x²+7
f est un polynome de 3ieme degrée donc dérivable au moins deux fois et tu as
f'(x)=3x²-24x
f"(x)=6x-24=6(x-4)
donc f"(x)=0 ssi x=4

cela ne veux pas dire pour autant que I(4;f(4)) est centre de symétrie de Cf.

mais dans le cas des polynome de 3ième degré le point d'inflexion est centre de symétrie.

donc pour f(x)=x¨3-12x²+7 le point I(4;f(4)) est centre de symétrie de Cf.

et tu as f(4)=4^3-12*16+7=65-192=-121

Et cette règle utilisant les dérivés ne correspond qu'aux polynômes ?

Si cette formule n'est pas sûre je ne préfère pas l'utiliser

f(x)=x³-12x²+7

Le point P(a ; f(a)) est centre de symétrie si on a : f(a-x) + f(a+x) = 2.f(a)
-----
f(a-x) = (a-x)³ - 12(a-x)² + 7
f(a+x) = (a+x)³ - 12(a+x)² + 7

f(a-x) + f(a+x) = (a-x)³ - 12(a-x)² + 7 + (a+x)³ - 12(a+x)² + 7

f(a-x) + f(a+x) = a³ - 3a²x + 3ax² - x³ - 12(a²-2ax + x²) + 7 + a³ + 3a²x + 3ax² + x³ - 12(a²+2ax+x²) + 7
f(a-x) + f(a+x) = 2a³ + 6ax²  - 24a² - 24 x² + 14
f(a-x) + f(a+x) = 2(a³ + (3a-12)x² - 12a² + 7)

---> il faut que a³ + (3a-12)x² - 12a² + 7 = f(a)

a³ + (3a-12)x² - 12a² + 7 = a³-12a²+7

---> (3a-12)x² = 0 Et ceci doit être vrai pour tout x de R

Et donc, on doit avoir 3a-12 = 0, soit a = 4

f(a) = f(4) = 4³ - 12*4² + 7 = -121

---> le Point P(4 ; -121) est centre de symétrie de la courbe représantant f(x) = x³-12x²+7
-----
Sauf distraction.  

Zut pour mon orthographe.

Merci

Le centre de symétrie ne se trouve pas toujours sur la courbe (je pense aux fonctions rationnelles) comment on fait dans ce cas, car l'égalité  f(a-x) + f(a+x) = 2.f(a) n'est pas valable

Concernant les fonctions rationnelles, tu as eu plusieurs réponses concernant les fonctions homographiques ici : fonction homographique
Visiblement ça marche.

dans le cas général
(a,b) est centre de symétrie de Cf courbe de f si f vérifie deux conditions:
la première: son domaine de définition doit être centré sur a. Cette condition est souvent oubliée;
la deuxième: M(x;f(x)) et M(x';f(x')) deux point quelconques sont symétriques par rapport à (a,b).

dans ce cas; on doit avoir
a milieu de x et x': donc a=(x+x')/2 donc x'=2a-x
b milieu de f(x) et f(x'): donc b=(f(x)+f(x'))/2 donc f(x')=2b-f(x)
donc f(2a-x)+f(x)=2b
ici b n'est pas forcément égal à f(a) cad (a,b) n'appartient pas forcément à Cf.

Bonjour

Par simple souci d'équité, je signale aux participants de ce topic, qu'on critique ici certaines interventions!

Et bien moi, je ne suis pas d'accord avec ces critiques.

Il ne s'agissait pas ici de traiter tous les cas qui peuvent se présenter (comme par ex le cas où P n'est pas un point de la courbe représentant f(x)), mais bien de montrer comment dans le cas particulier de l'exercice, les coordonnées du centre de symétrie avaient été trouvées.

Et c'est ce que j'ai fait.

Libre à qui le veut de traiter le cas général quand ce n'est pas utile pour le problème posé, mais cela n'a évidemment rien d'obligatoire.

Je complète mon message précédent :

Première remarque sur l'énoncé : ce n'est pas la fonction qui a un centre de symétrie mais bien la courbe représentée par la fonction.

La fonction donnée dans l'énoncé est continue sur R et c'est donc dans ce cas particulier que ma réponse a été donnée.

Si on veut "généraliser" on peut le faire, mais alors, pourquoi s'arrêter aux courbes représentées par des fonctions dont le domaine d'existence n'est pas connexe ?

La notion de centre de symétrie de courbes ne s'arrète pas aux courbes représentées par des fonctions, elle peut s'étendre par exemple à des paraboles à axe oblique par rapport aux axes du repère ou à des ellipses ou a plein d'autres choses...

Et pourquoi s'arrêter à des courbes planes ?

Bref, on peut répondre en se limitant dans le domaine de l'énoncé posé (ce que j'ai fait en limitant a des courbes représentatives de fonctions continues dans R comme le permettait l'énoncé), c'est la méthode la plus facile à comprendre pour le "novice".

Ou bien, on peut répondre de manière plus globale (mais où limiter cette globalisation ? ), et évidemment plus on pousse loin la globalisation, plus la complexité augmente.