Inscription / Connexion Nouveau Sujet
Fonction ln
Bonsoir
Partie A:Étude d'une fonction auxiliaire
Soit g la fonction définie sur]0;+
par g(x)=((lnx)/(x))+e
On note Cg la courbe qui représente la fonction g dans le plan muni d'un repère orthonormal.
1)Déterminer lim g(x) quand x
0- et lim g(x) quand x+.
Que peut-on en déduire pour Cg?
2)Déterminer a l'aide de la fonction dérivée g', le sens de variation de g.Dresser le tableau de variation de g
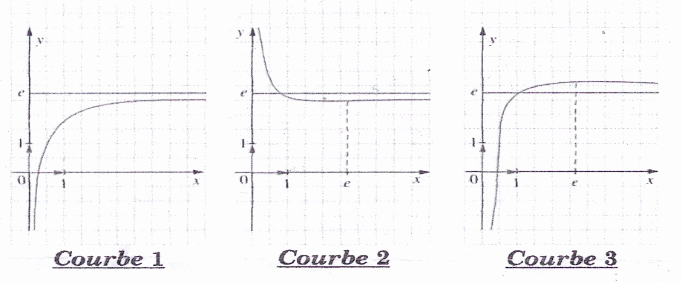
3)L'une des trois courbes ci-contre est la courbe Cg.Indiquer en justifiant votre choix celle qui représente la
fonction g
4)Calculer g(1/e).En déduire pour tout x appartenant a ]0;+ le signe de g(x)
Partie B:Étude d'une fonction et tracé de sa courbe représentative
Soit f la fonction définie sur]0;+ par f(x)=1/2*(lnx)²+ex-e
On note Gf la courbe qui représente la fonction f dans le plan rapporté a un repère orthogonal (0;
;
)(unités graphiques:4 cm en abscisse et 2 cm en ordonnées)
1)Vérifier que pour tout x de ]0;+ , f'(x)=g(x)
2)Déterminer lim f(x) quand x0+ et lim f(x) quand x+
3)dresse le tableau de variation de f
4)Déterminer une équation de la tangente T a Cf au point d'abscisse 1.Préciser la position de T par rapport a Cf
Partie C:
1)Soit H la fonction définie sur ]0;+ par H(x)=x(lnx)²-2lnx+2x
Soit h la fonction définie sur ]0;+ par h(x)=(lnx)²
Vérifier que H est une primitives de h sur ]0;+
2)En déduire une primitive F de f sur ]0;+
Pouvez-vous m'aider
S.V.P
Hello,
il y a un exercice qui ressemble au tien ici : 
Logarithme neperien
Une équation de la tangente au point d'abscisse a s'écrit ( voir cours ) :
y=f'(a)(x-a)+f(a)
mais vérifie quand même.
Si H(x) est une primitive de h(x), en dérivant H(x) tu dois retrouver h(x). Donc dérives H(x) et dis moi ce que tu trouves.
Ah non non 
dans ton énoncé il n'y a pas de facteur x avec ln x.....et si on dérive H(x) de ton énoncé on ne trouve pas h(x). Tandis qu'avec MON H(x) ça fonctionne. Donc revérifies l'énoncé STP.
excuse moi
dans le message précèdent je voulai dire que tu avait raison j'avais oublier le facteur x
tu trouve une primitive de chaque terme c'est tout.
Une pour 1/2 (ln x)2 en utilisant la question précédente.
Une pour ex...facile.
Une pour e....très facile.
Tu ajoutes tout ça et une constante et c'est bon.
d'après la question 1) C une primitive de (ln x)2 c'est :
x(ln x)2-2x ln x+2
rappelle toi...une primitive de h(x) c'est H(x).
Annuler
connectez vous