Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Fonction LogarithmeTopics traitant de Fonction Logarithme [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Fonction ln

Posté par
Ayato 31-12-15 à 13:06

Hello,

J'aimerai bien qu'on me corrige sur un exercice assez long sur la fonction logarithme népérien merci ^^.

Partie 1
U une fonction dérivable sur ; où U2=U.U
a)Démontrer que si U à comme dérivée U' , alors (U2)' =2U'.U

b) En déduire que si g est définie par g(x)= (lnx)2 ; alors g'(x)=2 lnx/x

Mes réponses :

a) On sait que (U2)'= (uxv)'= u'v+uv'      
Or, U2=UxU
Donc par identification v=U  
Ainsi (uu)'=(uv')

Or (uxv)'=u'v+uv' (uu)'=u'v+uv'
                                                                                                  =u'u+uu'
                                                                                         (uu)'=2u'u
Cqfd
Je ne sais pas trop si c'est bon car en faite j'ai considéré que U=u et v=U
or par exemple si : uv=U.U=100
u=50 v=2  et U=10
Donc c'est un peu faux ?
Ah moins que comme c'est le produit qu'on prend ? Je ne sais pas trop

b)On a montré que (U2)'=2U'U

g(x)=(lnx)2 g'(x) = 2(lnx)'lnx

Or (lnx)'=1/x   g'(x)= 2(1/x)lnx
                                                                                g'(x)= 2lnx/x

Cqfd

Partie B

Soit f la fonction définie sur R+* par : f(x)= ((1+2lnx)/(x))-2  où -2+(1+2lnx)/(x) pour être plus lisible ^^
c) Démontrer que f tend vers l'infini au voisinage de 0

d) Quelle est la limite de f au voisinage de + ? Justifier

e) Quelle interprétation graphique faites -vous des deux précédents résultats?

f) Démontrer que f est dérivable susr ]0;+[ de dérivée f'(x)=(1-2lnx)/(x2)

g) En déduire les variations de f ; puis résumer vos résultats dans un tableau de variations.

h) Calculer l'abscisse du pint d'intersection de la courbe de f avec la droite d'équation y=-2

i) En vous aidant de votre calculatrice, tracer l'allure de la courbe de f avec ses asymptotes, si elle en possède

j) Que peut-on dire du signe de la fonction f? Justifier

Mes réponses :

c) f(x)=((1+2lnx)/x ) -2
  
  lim ((1+2lnx)/x ) -2                            (1+2lnx)/x ) -2
x0                              
                                                                     (x((1/x)+2ln)/(x(1))-2

                                                         ((1/x)+2ln)/1)-2

Or, lim 1/x =
        x0
         lim 2ln=2ln                    
         x0

lim ((1/x)+2ln)/1)-2 = -2=
x0

Cqfd
Donc Cf admet une asymptot d'équation y=

d) lim ((1+2lnx)/x)-2
    x+

On remarque que  ((1+2lnx)/x)-2= (2lnx/x)+(1/x)-2 x0
Or, lim lnx/x =0                par produit lim 2lnx/x=0
       x+                        x+


0+0-2=-2

Donc lim f(x)=lim ((1+2lnx)/x)-2 =-2
             x+
Donc Cf admet une asymptot d'équation y=-2
e) Je ne sais pas vraiment sur la calculatrice on dirait une partie de fonction inverse négative.

f) f(x)=((1+2lnx)/x)-2

On remarque que f=u/v avec pour tout x appartenant à R+*

(u/v)=((u'v-uv')/v2)  avec u=1+2lnx  ; u'=2/x ; v=x ; v'=1

f'(x)= ((2/x)x-(1+2lnx)(1))/x2
         = (2-1-2lnx)/x2
f'(x) = (1-2lnx)/x2

Cqfd

g) On obtient les variations de f grâce à sa dérivée :
f'(x) = (1-2lnx)/x2      x>0

f(0) =-2 Enfin je sais pas trop comment faire la je bloque..

f) Non plus

i) J'ai pas compris ce qu'il demande là ? Faut refaire le graphique sur ma feuille ?

j) ...

Merci pour votre aide et Bonne fête de fin d'année

Posté par
Ayatore : Fonction ln 31-12-15 à 14:36

Partie 3

Soit F la fonction définie sur R+* par F(x)=lnx+(lnx)2-2x
Le but est de résoudre l'équation (E) : lnx+(lnx)2-2x=0

k) Démontrer que F est dérivable et que x>0 F'(x)=f(x)

l) En déduire les variations de F puis dresser une tableau de variation de F sans besoin de préciser ses limites au bornes de son ensemble de déf

m) Calculer F(1) et F(e-2) où e est le nombre définie par ln(e)=1

n) Montrer que l'équation (E) admet une solution unique notée x0 dans l'intervalle [e-2;1]

o) En vous aidant de votre calculette, déterminer une valeur approché de x0
à 0.001 près. Justifier explicitement.

k) x>0
F(x)=lnx+(lnx)2-2x

On remarque que F= (u+v)' =u'+v'

Avec u=lnx+(lnx)2 u' =(1/x)+(lnx)2'

Or, avec la formule de la partie 1 où (U2)'=2U'.U
On a : u'=(1/x)+(2/x)lnx= (1+2lnx/x)

et v= -2x v'=-2

Qui donne F'(x)=((1+2lnx)/x)-2
Cqfd

l)On obtient les variations de F grâce à sa dérivée x>0
(1+2lnx)/x)-2=0
(1+2lnx)/x)    =2
2lnx +1 = 2x
2lnx = 2x-1
2 = e2x-1

J'arrive pas à faire mon tableau...

m)  F(1)= ln1+2ln1-2
         F(1)= 0 + 0 -2 =-2

F(e-2)= ln(e)+2ln(e)-2e
                                      = 1+2-2e
F(e  -2)=3-2e

n) J'y réfléchis encore

o) Pareil

Posté par
Ayatore : Fonction ln 31-12-15 à 15:12

Up s'il vous plaît !

Posté par
Ayatore : Fonction ln 31-12-15 à 15:36

Up

Posté par
Ayatore : Fonction ln 31-12-15 à 16:29

Up

Posté par
Labore : Fonction ln 31-12-15 à 16:33

Bonjour,

Citation :
Je ne sais pas trop si c'est bon car en faite j'ai considéré que U=u et v=U
or par exemple si : uv=U.U=100
u=50 v=2  et U=10
Donc c'est un peu faux ?
Ah moins que comme c'est le produit qu'on prend ? Je ne sais pas trop


Tu n'as pas pris des fonctions mais des réels ...

partie  B

(x((1/x)+2ln)/(x(1))-2   ????


                                                        

Posté par
Ayatore : Fonction ln 31-12-15 à 16:46

Ah oui merci !

Pour la partie B je reconnais que ce n'est pas très lisible j'ai factorisé dénominateur et numérateur pour faire partir les x afins  d'enlever l'indétermination

Posté par
Labore : Fonction ln 31-12-15 à 16:55

partie B

f(x)=\dfrac{1+2ln(x)}{x}-2

f(x)=\dfrac{1+ln(x)}{x}+\dfrac{ln(x)}{x}-2

\lim_{x\to 0}\dfrac{1+ln(x)}{x}=1

\lim_{x\to 0}\dfrac{ln(x)}{x}=-\infty

\lim_{x\to 0}f(x)=-\infty

Posté par
Ayatore : Fonction ln 31-12-15 à 17:06

Merci mais je ne comprend pas pourquoi c'est - à l'avant dernière ligne car ça pourrait aussi être + non ?

Sinon vu que c'est pas très lisible j'ai recopié tout le sujet sur paint

Posté par
Ayatore : Fonction ln 31-12-15 à 17:12

Etant donné que je n'arrive pas à atacher voici l'énoncé en plus clair :
***lien supprimé***** image supprimée ** [/url]

Posté par
Labore : Fonction ln 31-12-15 à 17:12

Ok pour la limite en +∞

Citation :
e) Quelle interprétation graphique faites -vous des deux précédents résultats?

   c'est là que tu parles des deux asymptotes l'axe des y et la droite y=-2
dérivée Ok
signe de la dérivée
f'(x) = (1-2lnx)/x2  
signe de 1-2ln(x) ,x>0
1-2ln(x)>0
ln(x)<0,5
eln(x)<e0,5
x<e0,5
je viens de voir ton message ;
quand x tend vers 0 alors  ln(x) tend vers -∞
je regarde la auite

Posté par
Ayatore : Fonction ln 31-12-15 à 17:13

http://www.noelshack.com/2015-53-1451578338-nouvelle-image-bitmap-10.png

Posté par
Labore : Fonction ln 31-12-15 à 17:16

non pas de scan d l'énoncé ... ni http ce n'est pas autorisé sur ce site ,
j'arrive à lire ce que tu as tapé ..

Posté par
Labore : Fonction ln 31-12-15 à 17:17

Citation :
g) En déduire les variations de f ; puis résumer vos résultats dans un tableau de variations.

je pense que   ça doit  être OK  puisque tuas le signe de f' et les limite de f

Posté par
Ayatore : Fonction ln 31-12-15 à 17:19

Merci je fais le tableau de variation.

Ok désolé.

Posté par
Labore : Fonction ln 31-12-15 à 17:23

Citation :
h) Calculer l'abscisse du point d'intersection de la courbe de f avec la droite d'équation y=-2

il faut résoudre
f(x)-2=0
puis  souviens-toi que
eln(x)=x
le point d'intersection  est    situé lorsque f est croissante ...
Citation :
i) En vous aidant de votre calculatrice, tracer l'allure de la courbe de f avec ses asymptotes, si elle en possède

ou avec geogebra ( logiciel gratuit )
Citation :
j) Que peut-on dire du signe de la fonction f?

   justifie que la courbe admet un maximum    et précise son signe .

Posté par
Labore : Fonction ln 31-12-15 à 17:33

partie 3)
tu as dû remarquer que la dérivée  de F est la fonction f  , dont tu viens de déterminer le signe...( négatif )
( mais comme tu  n'avais pas  répondu à la dernière question de la partie 2...)
je pense que ça doit être Ok pour toi

m)  Ok pour F(1)=-2
  F(e^{-2})=ln(e^{-2})+(ln(e^{-2}))^2-2e^{-2}
refais le calcul

Posté par
Ayatore : Fonction ln 31-12-15 à 17:36

Merci
h) f(x)-2=0
-2-2+(1+2lnx)/x2 =0
-4+(1+2lnx)/x2=0
(1+2lnx)= 4x2
ln x = 2x2-0.5
elnx=e2x²-0.5
x= e2x²-0.5

On peut le faire partir le e encore ? Ou c'est bon comme ça ?

i) Certes j'ai compris ça mais je vois pas ce qu'il faut que je mette comme réponse

j) J'y réfléchis

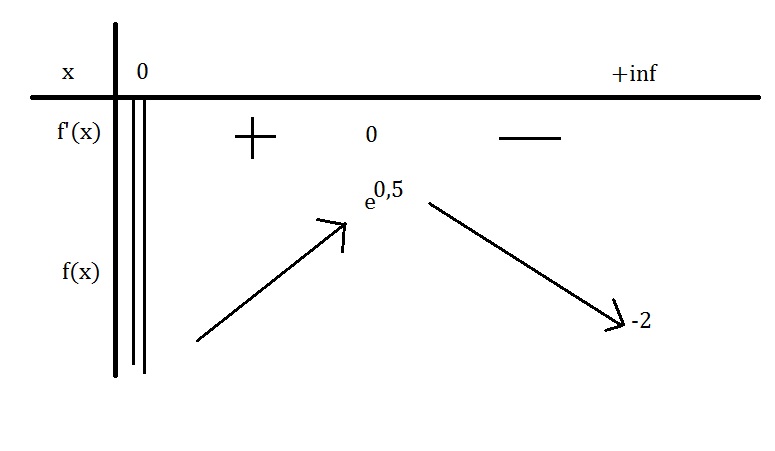
Fonction ln

Posté par
Ayatore : Fonction ln 31-12-15 à 17:44

J'arrive pas à répondre à la h je crois que mon tableau est faux..

D'ailleurs j'ai oublié la borne en 0 qui est -

Posté par
Ayatore : Fonction ln 31-12-15 à 17:54

F(e^{-2})=ln(e^{-2})+(ln(e^{-2}))^2-2e^{-2}
F(e^{-2})=-2 -2*-2-2e^{-2}            
F(e^{-2})=2-2e^{-2}

Je sais pas trop comment faire partir l'exposant là

Posté par
Labore : Fonction ln 31-12-15 à 17:56

oups  j'avais fait une erreur de signe
il faut que f(x)=-2  avec  x>0
d'où f(x)+2=0
\dfrac{1+2ln(x)}{x}-2+2=0

\dfrac{1+2ln(x)}{x}=0

1+2ln(x)=0 \\ \\ 2ln(x)=-1 \\ \\ ln(x)=-0,5 \\ \\ e^{ln(x)}=e^{-0,5} \\ \\ x=e^{-0,5} \\ \\

Posté par
Labore : Fonction ln 31-12-15 à 18:00

F(e-2 )=2-2e-2 = OK
puis pour justifier  que c'est un nombre positif
2(1-\dfrac{1}{e^2})=2(1-(\frac{1}{e})^2)>0

Posté par
Ayatore : Fonction ln 31-12-15 à 18:11

J'essaye la n :

f est continue
f est décroissante
D'après le théorème des valeurs intermédiaires appliqué au cas des fonctions strictement monotones, l'équation (E)=0 admet une unique solution (notée α ) sur [e-2 ; 1]
De plus f coupe x en -2 cette solution se situe donc entre 3 et 1

et la o j'y réfléchis

Je me demandais c'esst normal qu'à aucun moment on a jamais calculé f(0) où f(de quoi que ce soit) ?

Posté par
Labore : Fonction ln 31-12-15 à 18:15

Fest continue
Fest décroissante
F(e-2>0 et F(1)<0
D'après le théorème des valeurs intermédiaires appliqué au cas des fonctions strictement monotones, l'équation (E)=0 admet une unique solution (notée α ) sur [e-2 ; 1]

Citation :
De plus f coupe x en -2 cette solution se situe donc entre 3 et 1

je ne comprends ce que tu veux dire

Posté par
Ayatore : Fonction ln 31-12-15 à 18:24

Ah oui j'avais oublié F(e-2) et F(1) Merci

Non rien j'ai juste dû fantasmer..

Pour la o je peux utiliser le graphique de la calculatrice mais ce sera pas à 0.001 près je peux faire autrement ?
Et, est- ce que tu peux me guider sur la i et la j merci.

Posté par
Ayatore : Fonction ln 31-12-15 à 18:26

Plus je fais le tableau de variation de la l

Posté par
Ayatore : Fonction ln 31-12-15 à 18:31

.

Fonction ln

Posté par
Labore : Fonction ln 31-12-15 à 18:34

Citation :
Je me demandais c'esst normal qu'à aucun moment on a jamais calculé f(0) ou f(de quoi que ce soit) ?


on a jamais calculé f(0)   heureusement car ln(0)

f(de quoi que ce soit) ? tu aurais dû calculer f(e0,5)
pour montrer que f <0 pour tout x
d'ailleurs sur ton tableau corrige f' s'annule pour e0,5 ( et non 0)
  pour f le maximum f(e0,5)=(2-2*e0,5)/e0,5-0,79 et non e0,5
n'oublie pas  le -∞ et le -2

Posté par
Ayatore : Fonction ln 31-12-15 à 18:47

Je crois que mon tableau est bon là normalement.


tu aurais dû calculer f(e0,5)
pour montrer que f <0 pour tout x
  pour f le maximum f(e0,5)=(2-2*e0,5)/e0,5-0,79 et non e0,5
[/quote






Mais je ne comprends faire ça dans quel but ?

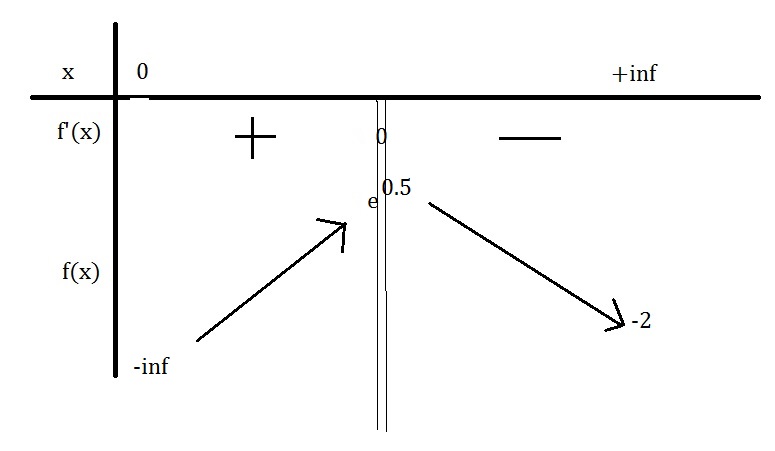
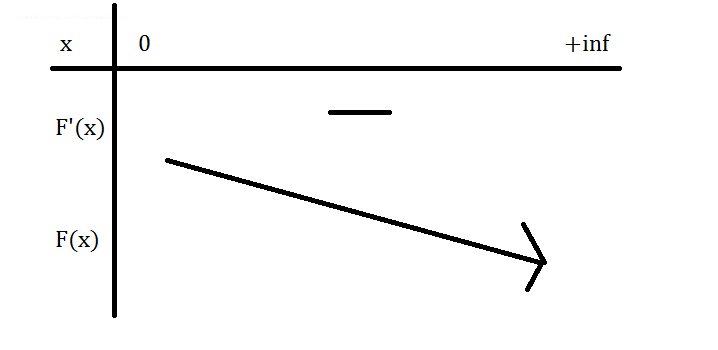
Fonction ln

Posté par
Labore : Fonction ln 31-12-15 à 18:59

corrige ton tableau de variations
  le maximum pour f  n'est pas e0,5 ,  e0,5 , c'est la valeur de x pour laquelle f' s'annule
les doubles barres sont au début  et non quand f'(x)=0

sur 1ere la ligne  x   0 ( n'oublie pas les doubles barres  0 valeur interdite) e0,5    puis +∞

  ensuite signe def' +       0 ( sous le e0,5 )     puis-
   puis variation de f  (-∞)croissante         f(e0,5)     0,79  puis décroissante      -2      

Posté par
Ayatore : Fonction ln 31-12-15 à 19:06

Ah merci beaucoup pour ton aide je ferai la dernière sur geogebra bonne fête de fin d'année

Posté par
Labore : Fonction ln 31-12-15 à 19:10

Je suis obligée de m'absenter  jusqu'à samedi  .
  le tableau de variation de F
tu as oublié les double barres pour le 0

A samedi si nécessaire

Posté par
Ayatore : Fonction ln 31-12-15 à 19:12

Ah oui, oh ok merci encore.


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1760 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !