Inscription / Connexion Nouveau Sujet
fonction ln (sujet 1 ex 4 B)
Bonjour,
Voici l'exercice B du sujet 1 (exercice 4 au choix entre A et B)
On considère la fonction f définie sur l'intervalle ]0;+ [ par :
[ par :
f(x)= x+4-4ln(x)-3/x
où ln désigne la fonction logarithme népérien
On note C la représentation graphique de F dans un repère orthonormé
1) déterminer la limite de la fonction f en + 
2) on admet que la fonction f est dérivable sur ]0;+ [ et on note f ' sa fonction dérivée
[ et on note f ' sa fonction dérivée
Démontrer que, pour tout nombre réel x>0 on a :
f '(x)=(x²-4x+3)/x²
3 a) Donner le tableau de variation de la fonction f sur l'intervalle ]0;+ [
[
On y fera figurer les valeurs exactes des extremums et les limites de f en O et en + 
On admettra que lim f(x)=- 
x 0
0
b) par simple lecture du tableau de variations, préciser le nombre de solutions de l'équation f(x)=5/3
4) Etudier la convexité de la fonction f c'est-à-dire préciser les parties de l'intervalle ]0;+ [ sur lesquelles f est convexe et celles sur lesquelles f est concave
[ sur lesquelles f est convexe et celles sur lesquelles f est concave
On justifiera que la courbe C admet un unique point d'inflexion dont on précisera les coordonnées
Voilà ce que j'ai essayé de faire
1)
lim ln(x)= + 
x +
+
lim x+4= + 
x +
+
je ne sais pas quoi faire pour le reste
lim f(x) = + 
x +
+
2) f est dérivale sur ]0;+ [
[
x dérivée 1
4ln(x)dérivée 4/x
3/x dérivée -3/x²
donc f '(x)= 1-4/x-(-3/x²) = (x²-4x+3)/x²
3a)
x 0 1 +
f '(x) + 0 -
f(x) - flèche montante 2 flèche descendante +
flèche montante 2 flèche descendante +
3b)
je ne sais pas trop comment faire
pour moi je pense qu'il n'y a qu'une solution de l'équation f(x)=5/3
4)
la fonction f est convexe sur ]0; 2,5] et concave sur [2,5 ; +  [
[
la courbe C admet un unique point d'inflexion dont les coordonnées sont (1 ; 2)
MERCI
Puisque la parenthèse tend vers 1 lorsque x tend vers
2
Remarque la dérivée étant aussi simple on gagne du temps en l'écrivant directement
3) après factorisation () et la suite)
Signe de
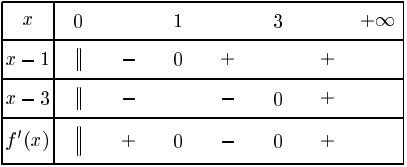
tableau de variations
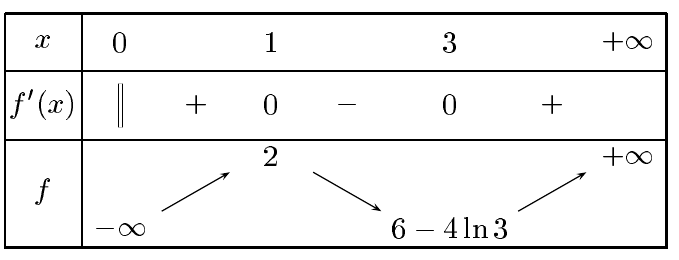
b) En lisant le tableau de variations l'équation admet 3 solutions
Remarque : une fonction ne peut décroître vers C'est un moyen de contrôle. Il y a donc une erreur quelque part
4 Dérivons
La dérivée seconde s'annule en
Si par conséquent la fonction est convexe sur
Elle est donc concave sur
la courbe représentative de admet donc en
un unique point d'inflexion
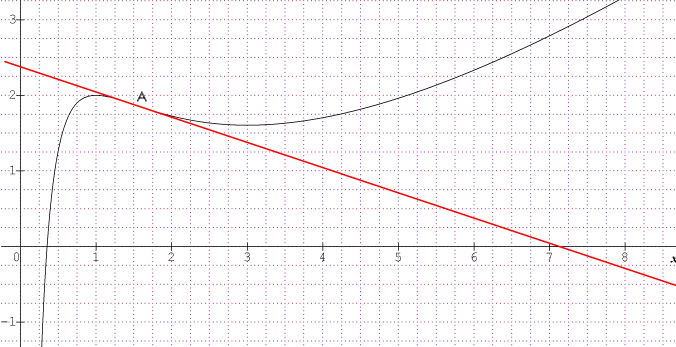
En rouge la tangente au point d'inflexion
tu vois hekla que j'ai beaucoup de mal
pour la question 3 je n'aurai pas pensé de factoriser. Comment faire pour savoir qu'il faut factoriser ?
pour 3 b ) comment vois-tu qu'il y a 3 solutions ?
pour le 4)
il faut toujours calculer la dérivée seconde pour savoir si la courbe est concave ou convexe ?
le point d'inflexion et donc 3/2
quels sont les coordonnées ? (moi je pense à 3/2;1,9 ?)
MERCI
On veut les valeurs qui annulent comme on n'a pas du premier degré la seule issue est la factorisation
une solution sur chacun des intervalles j'avais mis une valeur approchée pour bien le montrer
Toujours le bon vieux TVI en allant de à 2 on passe bien par
sur le second intervalle on descend de 2 à environ 1,60 donc là aussi on passe bien par 5/3 et sur le dernier on va de 1,60 à donc on passe bien aussi par 5/3
donc 3 solutions
Oui, c'est la définition une fonction est convexe sur I si pour tout
Point d'inflexion en valeur exacte


