Inscription / Connexion Nouveau Sujet
fonction logarithmique
Bonjour,
j'ai la fonction f(x)=-x + ln (2x+2) - ln (x+2)
Je dois justifier que f(x) n'existe que pour x appartenant à ]-1;+∞[
Je ne sais pas comment faire
Merci d'avance de votre aide
vous avez bien dû étudier la fonction et apprendre qu'elle n'est définie que pour les réels strictement positifs
ou on ne ne peut prendre le logarithme d'un nombre que si celui-ci est strictement positif
vous avez donc à résoudre
votre profil indique seconde dans ce cas vous ne devez pas avoir entendu parler de logarithme
sinon il serait bien de modifier votre profil
oui, et qu'avait écrit hekla aussi :
vous avez donc deux inéquations à résoudre et intersection des ensembles solutions
donc tu dois maintenant prendre tous les x qui vérifient en même temps tes deux inéqutions
je vous l'ai dit prendre l'intersection des deux ensembles
que vaut ?
et vous aurez répondu à votre question
Bonjour,
J'ai une fonction f(x)=-x + ln (2x+2) - ln (x+2)
a) je dois déterminer la limite de cette fonction en -1
J'ai trouvé la limite en -2,75.
Est ce bien ça ?
b)f(x) est aussi égal à -x + ln2 + ln(x+1/x+2) et g(x) = -x + ln2
Je n'arrive pas à montre que f(x)-g(x)=0 quand x tend vers +inf
Merci de votre aide
*** message déplacé ***toutes les questions d'un même exercice doivent être posées dans le même sujet
J'ai trouvé la limite en -2,75.
qu'est-ce que cela veut dire ?
que vaut la limite de la fonction
La limite de la fonction ln quand x tend vers 0 vaut -inf
J'avais trouvé que lim f(x)=2,75 quand x tend vers -1
Ma limite lorsque x tend vers -1 est donc de -inf
Pour la question b, je trouve une FI mais je n'arrive pas à factoriser après
Merci de votre aide
que vaut
certes forme indéterminée mais vous pouvez alors mettre en facteur au numérateur et au dénominateur et simplifier
\displaystyle \lim_{x\to +\infty}\dfrac{x+1}{x+2} je ne comprends pas comment on peut faire la factorisation avec x car le ln me pose problème
je n'avais pas parlé du logarithme mais uniquement de la fraction
on en fait autant avec
on simplifie la fraction par
on cherche alors qu'obtenez-vous comme réponse ?
après seulement on va considérer le logarithme
x+2 = x(2+2/x)
x(1+1/x) = +inf
x tend vers +inf
x(2+2/x)= +inf
x tend vers +inf
lim (x+1)/(x+2)=FI
x tend vers +inf
Désolé j'avais oublié de simplifier la fraction par x.
1/0 tend vers +inf et ln 1= 0
donc lim -x + ln2 +ln (x+1/x+2)+x -ln 2 tend vers 0
x tend vers +inf
Est ce bien ça ?
Ce que je voulais dire c'est ce que vous venez d'expliquer qui est bien plus clair que ce que j'avais écrit.
Comment resoud t-on l'inéquation:
ln((x+1) / (x+2)) ≥ 0 sur ]-1;+inf[
On prend l'exponentielle des deux membres
ce qui revient à résoudre
remarque : le dé sert à coudre on résout simplement
ce n'était pas la réponse attendue
l'ensemble des solutions de l'inéquation est
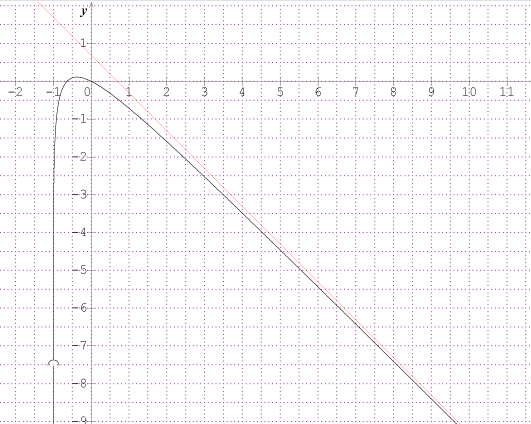
par conséquent la courbe représentative de est située en dessous de la droite représentative de
de rien
il doit vous rester les représentations graphiques mais cela ne devrait pas poser de problème
Merci
Il me reste encore deux parties dans cet exercice
Je reviendrais vers ou si j'ai un problème 
Merci de toute votre aide qui m'a bien aidé
Juste une dernière question:
lorsqu'on me dit de représenter la droite T qui fait -0,5x ; les asymptotes et C dans le repère d'unité 4 cm en abscisse et 8 cm en ordonnée, je dois représenter quoi exactement ?
Je dois representer f(x), f'(x), g(x) ou pas ?
C doit être définie dans le texte cela devrait être la courbe représentative de
les asymptotes sont et
quant à T ce n'est pas une équation de droite que vous donnez, à quoi correspond-elle ?
Je me suis trompé désolé
Comment dois-je procéder pour passer de:
((x+1)*ln(2x+2)-(x+2)*ln(x+2)) à ln(2*(x+1))-ln(x+2)
Merci
Oui la question est :
justifier le deuxième résultat donné par le logiciel de calcul formel.
Ils ont mit ça dans le logiciel: ((x+1)*ln(2x+2)-(x+2)*ln(x+2))
et le logiciel a donné ça en réponse: ln(2*(x+1))-ln(x+2)
C'est possible que ce soit une dérivée ou une primitive car apres il me demande de résoudre un intégral donc je pense que ça doit être la primitive mais je ne suis pas sur
si vous ne donnez pas le texte il est difficile d'y répondre
le premier terme était la fonction et le second sa dérivée
par conséquent dérivez
La dérivée de x+1 est 1
la dérivée de ln(2x+2) est 2/2x+2
La dérivée de x+2 est 1
La dérivée de ln(x+2) est 1/2x+2
Je n'arrive pas à trouver la dérivée complète
Merci beaucoup j'ai trouvé
Pour la questiond'après, il me demande d'en déduire la valeur exacte de l'intégrale f(x)dx
Je dois calculer la primitive mais je ne sais pas du tout comment faire
À quoi sert la question précédente ?
vous venez de montrer que la dérivée de
était
par conséquent est une primitive de
vous savez calculer une primitive de et qu'une primitive de
est
où
et
sont des primitives de
et
Bonjour,
Voici les questions:
3 a) En déduire la valeur éxacte de
F(x)=ln(2*(x+1))-ln(x+2)
J'ai trouvé en réponse: ln8-ln5-ln4+ln3
Est ce bien ça ?
J'aimerais de l'aide pour la question 3 b svp
3 b )En déduire la valeur exacte en cm carré, de l'aire comprise en tre la courbe f(x), l'axe des abscisses, les droites d'équations x=1 et x=2
F(x)=ln(2*(x+1))-ln(x+2)
Merci de votre aide
*** message déplacé ***


