- Arithmétique dans Z - supérieur
- Exercice : le petit théorème de Fermat
- Ensemble et application Partie II
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Un best-of d'exos de probabilités (après le bac)
Inscription / Connexion Nouveau Sujet
Fonction partie entière par excès
Bonjour à tous,
Je suis actuellement en L1 MIASHS et bloque à la fin de mon projet maths.
Pourriez vous m'aider à démontrer la relation suivante.
Merci d'avance.
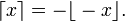
Soit x un nombre réel
La partie entière de -x est le nombre n relatif tel que n -x
-x n+1 .
n+1 .
En multipliant les inégalités par -1, on obtient que -n x
x -n-1 . En posant k=-n, il vient que k
-n-1 . En posant k=-n, il vient que k x
x k-1.
k-1.
A toi de conclure!!
Trop d'inégalités larges !
La partie entière d'un nombre est l'entier
caractérisé par
( et pas
pour la deuxième inégalité !).
La partie entière par excès d'un nombre est l'entier
caractérisé par
On sait que : ⌊x⌋ ≤ x ≤ ⌊x⌋ +1
→ -⌊x⌋ -1 < -x < -⌊x⌋
et que ⌈x⌉ -1 < y < ⌈x⌉
→ ⌈-x⌉ -1 < -y < ⌈-x⌉
On a donc par transitivité des inégalités : - ⌊x⌋ = ⌈-x⌉
→ ⌊x⌋ = - ⌈-x⌉
Ceci est-il bon ?
Merci pour vos réponses !
Je me suis trompé dans les inégalités :
On sait que : ⌊x⌋ ≤ x < ⌊x⌋ +1
→ -⌊x⌋ -1 < -x ≤ -⌊x⌋
et que ⌈x⌉ -1 < x ≤ ⌈x⌉
→ ⌈-x⌉ -1 < -x ≤ ⌈-x⌉
On a donc par transitivité des inégalités : - ⌊x⌋ = ⌈-x⌉
→ ⌊x⌋ = - ⌈-x⌉

 8
8
 arithmétique en post-bac
arithmétique en post-bac