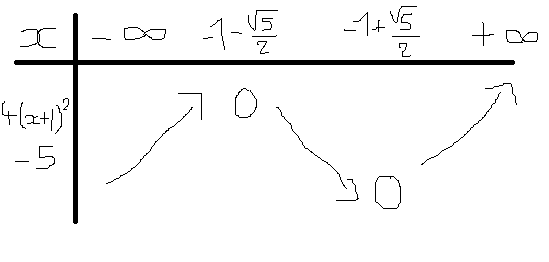Inscription / Connexion Nouveau Sujet
Fonction polynôme de degré 2
Salut, voilà mon exo a faire pour lundi, si quelqu'un peut m'aider :
On considère la fonction polynôme de degré 2, f définie sur R par f (x )= 4x²+8x-1.
1/ Vérifier que pour tout réel x, on a f(x) = 4(x+1)²-5.
2/a/ A l'aide des variations de la fonction carré, étudier les variations sur R de la fonction v : x -> (x+1)².
b/ En déduire les variations sur R de la fonction f.
3/a/ Déterminer les antécédents de 0 par f.
b/ En déduire le tableau des signes de f.
4/a/ Soit h un réel, comparer f (-1-h) et f (-1+h).
b/ Que peut-on en déduire pour la courbe représentative de la fonction f.
5/ Tracer la courbe de la fonction f sur l'intervalle [-4 ; 3].
J'ai seulement réussi a faire le 1/, pouvez-vous m'aider pour la suite ?
merci
salut!
tu as dû étudier en cours comment trouver les variations d'une fonction trinôme du second degré non?
pour les variations c'est ça.
la fonction dont on cherche les variations est très proche de la fonction carré non?
si on posait X=x+1, alors on connaît les variations de X^{2} :
décroissant jusqu'à X=0 puis croissant.
sauf que X=0 si et seulement si x+1=0 ssi x=-1
tu as donc les variations de ta fonction
non!
dans ton tableau de variations il faut juste mettre la ligne de (x+1)2
mais avant, tu dois expliquer comment tu les trouves les variations...
qu'est-ce que tu n'as pas compris?
donc il n'y a qu'une seule ligne, et c'est donc décroissant de - l'infini jusqu'à 0 et croissant de 0 jusqu'à + l'infini ?
oui il n'y a qu'une seule ligne
mais c'est pas en 0 que ça change de variations!
Relis la démonstration que je t'ai faite et dis-moi ce que tu n'as pas compris
et le -1 se met bien entre les flèches de variations ? car ça fait longtemps que je n'en est pas fait ^^
oui! sauf que la valeur en -1 change!
est-ce que tu saurais justifier pourquoi c'est le même tableau?
là tu n'as rien prouvé!
il faut juste dire que tu connais les variations de la fonction donc comme 4 est strictement positif, les variations de
sont les mêmes
bah vu que c'est les mêmes variations, elles changent pour x=-1
mais la valeur f(-1) n'est pas la même que sur l'autre tableau!
pourquoi tu veux rajouter des lignes!!
c'est pas un tableau de signe! un tableau de variations ça n'a qu'une seule ligne!
beh dans le passé, j'avais appris qu'il y avait plusieurs lignes dans le tableau c'est pour sa !
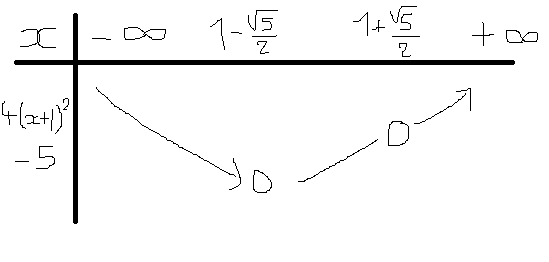
Pour la 3/a/, j'ai trouvé comme antécédents -1-V5 et -1+V5, est-ce bon ?
tu connais les variations de f,
tu sais où f s'annule
donc tu connais le signe de f!
essaye de trouver tout seul ça c'est pas compliqué
bah pas exactement!
là ce que tu as dit c'est que la fonction change de variation en 1-v(5)/2
d'ailleurs j'ai fait une erreur!!! c'est -1 v(5)/2 les solutions
v(5)/2 les solutions
donc tu en as une avant -1 et une après -1
donc ta fonction est positive, puis négative à partir de -1-v(5)/2 puis redevient positive à partir de -1+v(5)/2
la 4a est évidente! il suffit de faire le calcul!
la b. je te rappelle que si alors la courbe a un axe de symétrie qui est l'axe des ordonnées.
ici c'est pas tout à fait ça mais presque..
oula! pas du tout!!
tu dois calculer la valeur de la fonction en un point!
par exemple: f(0)=4(0+1)2-5
...
donc calcules f(-1+h) et f(-1-h) et tu vas remarquer quelque chose
pour ( -1-h ), j'ai trouvé h= - V5/2 et h= V5/2
pour ( -1+h ), j'ai trouvé h= V5/2 et h= - V5/2
c'est bon ?
pour ( -1-h )
je dois bien faire 4*(-1-h+1)²-5 ?
Donc ce qui ferait -4-4h+4-5
qui est égal à -4h-5 ?