Inscription / Connexion Nouveau Sujet
fonction t -> a sin(wt+phi)
Bonjour, je n'ai rien compris a ce qu'il faut faire.
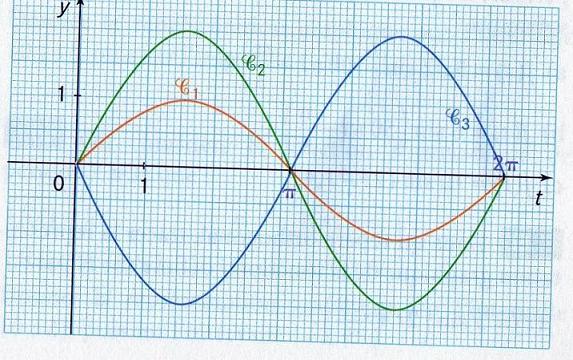
Dans un repère orthonormal, la courbe C1 est la représentation graphique sur [0;2
] de la fonction f telle que f(t)=sin t.
1. La courbe C2 est la représnetation graphique sur [0;2] d'une fonction f2 du type t
a sin (
t).
Donner l'expression de f2(t).
Je ne vois pas trop c'est quoi l'expression f(t)=a sin (t).
Mais c'est exactement ce qu'il y a dans le texte.
2. Les courbes C2 et C3 sont symétriques par rapport à l'axe des abscisses.
De quelle fonction f3 est-elle la courbe représentative?
Pour moi c'est l'inverse de f2 donc f3(-t)=a sin (-t).
Ecrire f3(t) sous la forme a sin (t+
).
Je suis encore plus plonger.
Merci de bien vouloir m'aiguiller.
Au revoir.
Salut,
pour la 1, il faut sans doute déterminer a. Tu peux par exemple remarquer que f1(3/2) = 1 et f2(3/2) = 2. Pour la 2, cherche tel que sin(t+) = -sin(t).
il faut que tu te serve des propriétés de la fonction sin :
f2()=0 
{a=0 ou w=k, avec k
}
or si a=0 alors f2(t)=0 sur [0,2] donc...
il ne faut surtout pas déterminer a en premier, ca serait un non sens, car si w
1 je vous souhaite bien du courage pour trouver 2 même a pour 2 points de [0,2] différents !
Merci pour les réponses mais je ne capte pas grand chose.
a est la valeur maximum.
c'est quoi exactement
pareil.
on le trouve comment.
t est a l'instant ou je veux le prendre.
Mais après ca me pose un petit problème pour trouver la bonne expression.
pour ma part
la verte est périodique de période 2pi, donc sa pulsation est la même que la rouge => w=1
son amplitude vaut 2 car verte=2rouge : y2=2sin(t)
bleue=-verte
y3=-2sin(t) = 2sin(t+pi) donc phi=pi (2pi près)
Rudy
Pour la Période 2 je suis sur.
1. Donc pour l'expression, je devais me reperer par rapport à la 1ère courbe.
f2(t)=2sin(t)
2. y3=-2sin(t) = 2sin(t+pi) donc phi=pi (2pi près)
Ta remplacer a par -2 pour la bleu et 2 ainsi que pour la vert.
Et aussi je voulais rajouter pour la fon c'est a sin (t+) avec a>0.
w c'est ce qui va te faire accélérer (ou décélérer) les pulsations de la fonction sinus :
sin(2t) est périodique de période ( elle va s'annuler en 0,/2,)
sin(t) est périodique de période 2( elle va s'annuler en 0,,2)
je crois qu'on l'appelle pulsation, nan?
a c'est l'amplitude, c'est-à-dire que sinus varie entre -1 et 1
mais a.sin(t) varie entre -a et a
donc tes oscillations vont être plus ou moins hautes avec ca
et phi c'est le déphasage, c'est-à-dire, que sin(t) vaut 0 en 0
mais sin(t-/4) vaudra 0 en /4 en fait ici pour avoir le graphe de cette fonction, il faudra décaler le graphe de sinus(t) par rapport aux abscisses de /4
Pour info :
tu as -sin(t)=sin(-t)
donc si a pouvait être négatif, ca te changerait les valeurs possibles de ton w !
tu aurais en effet a.sin(wt)=-a.sin(-wt)
et alors (a,w) et (-a,-w) seraient tous les deux solution
Le déphasage j'avais compris mais moi j'en vois pas de déphasage la ou sinon c'est de qui est déphasé.
Sinon avec les infos que tu me donne la réponse pour la 1. je pense que c'est
f2(t)=2sin(t) donc la avec le 2 on a 2 fois la 1ere courbe.
C'est bon ou pas?
De quelle fonction f3 est-elle la courbe représentative?
La fonction est f3(t)=-f2(t)=-2sin(t). C'est ca ou pas.
Ecrire f3(t) sous la forme a sin (t+) avec a > 0.
Si a peut être que possitif et que l'on ne peut pas changer a sin (t+),on peut faire comment?
Le déphasage j'avais compris mais moi j'en vois pas de déphasage la ou sinon c'est de qui est déphasé.
>>>s'il n'y en a pas elles atteignent leurs max en même temps... ce qui n'est pas le cas, f2 atteint son max en/2 et f3 en 3/2
(avec les zéros, c'est plus facilement exploitable) et tu remarques bien que si tu décales la courbe de f3 deou - tu retombe sur celle de f2
Sinon avec les infos que tu me donne la réponse pour la 1. je pense que c'est
f2(t)=2sin(t) donc la avec le 2 on a 2 fois la 1ere courbe.
C'est bon ou pas?
>>>>ca a l'air d'être ca, un graphe n'étant jamais hyper précis ^^
De quelle fonction f3 est-elle la courbe représentative?
La fonction est f3(t)=-f2(t)=-2sin(t). C'est ca ou pas.
oui ! sauf que je suppose qu'on va te demander la forme avec a>0
et donc un déphasage
Ecrire f3(t) sous la forme a sin (t+phi) avec a > 0.
Si a peut être que positif et que l'on ne peut pas changer a sin (wt+phi),on peut faire comment?
le déphasage, tu as f3(t+)=f2(t)
ou alors f3(t)=f2(t-)
donc f3(t)=2sin(t-)
Si a>0 alors ça doit donner :
f3(t)=-f2(t)=-2sin(t)=2sin(t+)
C'est bien ça?
Donc la sinon si c'est ca j'aurai fini.
merci déjà pour vos aides.
Annuler
connectez vous