Inscription / Connexion Nouveau Sujet
Fonction trigonométrie
Bonjour à tous,
Je coince sur mon dernier exercice d'un dm de math il s agit des fonction trigonométrie et je ne sais pas par où commencée 😥,
Voici l énoncer on considère la fonction sur R par: g(x) =cos ⁴(x)+2cos³ (x) +1
1) montrer que l on pet réduire le domaine de l étude de f(x) à l'intervalle [0;pie]
2) calculer la dérivée et donner le tableau de variation de la fonction sur l intervalle [0;pie]
Voici ce que j'ai commencer à faire mais je ne suis pas vraiment convaincu:
Pour la première question je me suis dit que c'est la fonction cos donc elle est périodique sur 2 pie et donc ça réduit le domaine de definition.
Pour la seconde j'ai trouver comme dérivée
-4sin³(x) - 6 sin² (x)
Mais pour le tableau de signe je sais plus du tout comment faire
J'ai chercher pour qu'elle x la fonction s annulé et j'ai trouver -1 mais je ne suis pas du tout convaincu...
Si quelqu'un aurait une méthode à me Proposer s'il voit plaît
Merci de m avoir lu et merci pour votre aide ! 🙂
Bonjour
1) 2pi est période, oui, mais montre aussi que ta fonction est paire
cela permettra de répondre à la question 1
modifie ton profil, tu n'es plus en terminale
Je ne faisais que passer et je laisse volontiers la main à qui peut aider. Merci. 
Mais le signe est étudier en fonction de la fonction de base et la dérivation en fonction de la dérivée ?
Je ne comprend pas pourquoi on factoriserai la dériver 😅
et je vien de me rendre compte de ma bêtise 😩 la fonction ne peut pas s'annuler en -1 puisque le tableau de signe et de 0 à pie..
Pour la dérivé je suis partie sur la formule
f^n = nf'f^n-1 donc
4 x -sin x cos⁴ + 6 x - sin x cos ²
= -4sin cos⁴ -6sin cos
Et donc il y a juste les cos qui manqués ?
Pour la dérivé je suis partie sur la formule
f^n = nf'f^n-1 donc
4 x -sin x cos⁴ + 6 x - sin x cos ²
= -4sin cos⁴ -6sin cos²
Et donc il y a juste les cos qui manqués ?
D'accord donc on factorisant par -2 cos²(x)
J'ai
(-2 cos²(x)) (2sin(x) cos(x) + 3 sin(x)
J'ai cos²x =2 ou 2sin (x) cos(x) =-3 sin (x)
Donc cos (x) = racine 2 ou - racine 2
Ou -2/3 cos =1 soit cos = 1+2/3
donc cos (x) = 5/3
Mais comment résoudre ces equation sachant que sur le cercle on ne peut pas avoir de cos(x) = racine 2 ou 5/3
Oui donc
(-2sin (x) cos²(x) )(2 cos(x) +3 )
Soit cos (x) =-3÷2
Ou
Sin(x)cos²(x)= 2
Toujours ce problème de résolutions 😓
Oui donc
(-2sin (x) cos²(x) )(2 cos(x) +3 )
Soit cos (x) =-3÷2
Ou
2Sin(x)cos²(x)= 0
Toujours ce problème de résolutions 😓
La première ligne est juste.
Dresse maintenant le tableau de signe de cette dérivée pour x variant de 0 à  .
.
X 0 pie
-2sin(x) cos²(x) -
2 cos(x) +3 +
G(x) -
Mais elle est sensé varier elle monte et après redescend ?
la dernière ligne ce n'est pas le signe de G, mais de la dérivée g'(x)
oui c'est juste
apprends à te vérifier avec geogebra ou autre logiciel
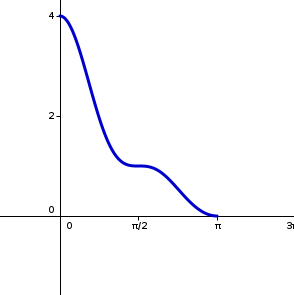
Donc G' est décroissante sur 0;pie
Donc ceci ne sert à rien de résoudre d equation
Mais pour admettre le sommet on peut le démontrer par calcul ?
Car pour finir le tableau de variation il faut les limites il me semble ?
g' est négative donc g est décroissante (programme lycée)
oui tu complètes avec valeur en 0 et valeur en pi bien sûr
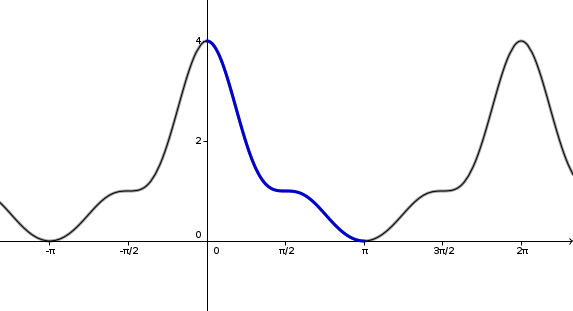
J'ai démontrer sur la question 1 que la fonction à un domaine de definition [0;pie ] en montrant qu'elle était périodique et symétrique
La courbe doit être tracer entre -pie et pie donc j'ai fait une courbe d'un courbe d un côté et l autre j'ai fait sa symétrique et après sa se répète mais ce n'est pas la consigne


 trigonométrie en post-bac
trigonométrie en post-bac