Inscription / Connexion Nouveau Sujet
fonctions
Bonjour, pouvez vous m'aider à faire cette exercice de maths svp ? pour la 1. je dois calculer f(-1) ? et ensuite ?
merci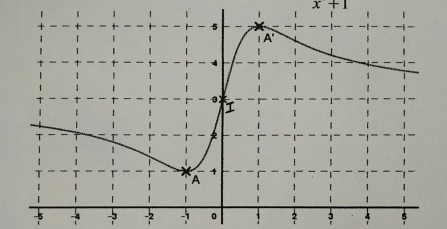
* malou > Image recadrée, sur la figure uniquement ! Si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum  *
*
bonjour, soit f la fonction définie sur R par : f(x)=ax^2+bx+c/x^2+1 représentée par (C) dans le repère
1) Déterminer les réels a,b et c (justifier par le calcul)
2) montrer que (C) admet une asymptote horizontale
POur la 1) comment puis je faire ?
merci
Sur ton graphique, il y a trois points marqués (A ; I et A').
Avec A, ça donne :
Cf passe par A(-1;1) donc f(-1) = 1 donc (a*(-1)²+b*(-1)+c)/((-1)²+1) = 1,
c'est à dire : (a-b+c)/2 = 1 donc a-b+c = 2.
fais pareil avec I et A'.
Avec I, ça donne :
Cf passe par I(0;3) donc f(0) = 3 donc (a*(0)²+b*(0)+c)/((0)²+1) = 1,
c'est à dire : (a-b+c)/1 = 3 donc a+b+c = 1.
Avec A', ça donne :
Cf passe par A(1;5) donc f(1) = 5 donc (a*(1)²+b*(1)+c)/((1)²+1) = 5,
c'est à dire : (a-b+c)/2 = 5 donc a+b+c = 2.
Ah non, là y'a pas besoin d'avoir eu cours dessus !!!
a*(0)²+b*(0)+c ça fait quoi ?
Et pour (a-b+c)/2 = 5 : si x/2 = 5 , alors x = ?
Oui
et
oui.
Donc, on reprend :
Avec A, on a trouvé : a+b+c = 2.
Avec I, on trouve : ....... ?
et avec A', on trouve : ........ ?
j'ai essayé autrement :
C=3 car f(0)=3
POur A : f(-1)=a-b+3/2=1 donc ca donne a-b+3=2
pour A' ; f(1)=a+b+3/2=5 donc a+b+3=10
a-b=-1 et a+b=7 ce qui donne a=b-1
donc b-1+b=7 qui donne 2b=8 et b=4 donc a = 3
Ce n'est pas "autrement" ça, c'est exactement ce qu'on a fait...
Comment expliques-tu ceci par exemple :
C=3 car f(0)=3



