Bonjour,
dans l'expression que tu trouves pour la dérivée, mets 3x en facteur  et pour étudier le signe de la dérivée c'est plus facile à faire à partir de sa forme factorisée.

comment sa 3x en facteur ? c'est sa que je ne comprend pas du tout !

tu trouves comme dérivée 6x-3x² on remarque que c'est aussi 3x*2-3x*x donc si tu mets 3x en facteur tu auras 3x*(2-x)=3x(2-x) c'est ce qu'il fallait trouver ...

d'accord j'ai compris merci , désolé j'

jai pas tro le sens de la logique .. et si je veux calculer le signe de la deriver je depend de quoi alors ? de 6x .. ou de  3x(2-x) .. ??

le plus facile pour le signe de la dérivée c'est de prendre la forme factorisée : f'(x) = 3x(2-x) et tu fais un tableau de signe.

disons que mon intervalle est [ -1 ; 3]
je pensais que pour trouver où elle s'annule il fallait faire: 3x (2-x)
3x= -2-x
x= 3/ -2-x = -1.5 - x
mais je ne croit pas que cest sa je n'arrive pas trop ..
et pour trouver le signe on doit bien remplacer -1 et 3 dans
3x (2-x) ?
pasque j'ai esayer de faire sa mais je trouve -9 a chaque fois sa peut pas etre tout le temps négatif il faut bien un positif ..

tu te trouves en situation d'un produit de deux termes, pour étudier le signe du produit tu étudies le signe de chaque terme puis tu fais le "produit des signes".
Donc :
première étape le signe de 3x
deuxième étape le signe de 2-x
finalement le signe de 3x * (2-x)

donc pour trouver le signe de 3x je fait si mon intervale est de -1;3
je fait 3 * -1 = -3

cest sa ? ou je fait autrement ? parce que si je fait sa et si je prend 3 pour 2-x je trouve aussi un nombre négatif ..

par exemple pour le signe de 3x tu commences par chercher 3x=0
3x = 0 ===> x=0 puis ensuite si x<0 de quel signe est 3x ? négatif
si x>0 de quel signe est 3x ? positif
ensuite dans ton tableau tu auras

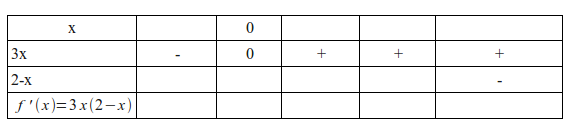
tu fais la même chose pour x-2 tu commences par x-2=0 ===> x= ?....

Mais pourquoi je remplace par 0 ? si je remplace toujours par 0 se sera toujours négatif ..

tu remplaces pas par 0 tu regardes de quel signe est 3x si x est inférieur à 0 ensuite de quel signe est 3x si x est supérieur à 0.

Tu fais la même chose pour 2-x tu cherches x tel que 2-x = 0 tu trouves 2 ensuite tu regardes de quel signe est 2-x pour des valeurs de x inférieures à 2, puis le signe de 2-x pour x supérieur à 2
Ainsi tu as déterminé le signe des deux termes de ton expression et tu peux conclure quant au signe de ton expression (en déterminant le signe du produit des deux)

olalala je comprend pas trop trop là :S
comment tu sais que je trouve 2 pour 2-x=0 ? et si je trouve 2 sa veut dire que cest positif?
et pour 3x je fait 3*0 = 0 cest sa ? donc sa ve dire que cest positif aussi ? mais cest pas possible que les deux soit possitif ..  désolé de t'embeter :s

tu comprends pas que je résous 2-x=0 ? et que je trouve x=2 puis si tu prends une valeur inférieure à 2, 1 par exemple l'expression est positive ? dans 2-x je remplace x par et j'obtiens 2-1=1 ce qui est positif ...
Tu es vraiment en terminale ?

je te mets le tableau de signes, essaye de voir comment on l'obtient, je reviens demain donc en cas de besoin n'hésites pas ...

oui je suis en terminal bac pro esthetique meme lool mais ma prof est merdique .. du cou voila , si j'ai bien compris que les deux sont positif seulment cest possible ? jpenser que il fallait un positif et un négatif

je comprends pas ta question

voilà pour illustrer le tableau de signes :

Enfete je comprend pas comment tu procède car dans mon exercice il me donne l'intervalle -1;3

donc je doit utiliser sa pour trouver le signe de la dérivée ? car à chaque fois j'utilise l'intervalle pour trouver le signe de la dérivée. et il faut que je trouve aussi où la dérivée s'annule .

l'intervalle n'apparaît pas dans ton premier message ...
ben dans ce que je t'ai noté, il faut que tu remplaces - par -1 et + par 3, cela ne change pas les résultats. Quant à ma manière de procéder je te l'ai indiquée hier dans mon message de 20:43 :
tu prends une valeur inférieure à 0 (-1 par exemple), tu regardes que quel signe est ton expression, puis tu prends une valeur comprise entre 0 et 2 (1 par exemple), tu regardes de quel signe est f(x) et finalement une valeur supérieure à 2 (3 par exemple)et tu regardes de quel signe et f(x). Si tu le fais correctement tu obtiendras les signes qu'il y a dans la dernière ligne de mon tableau.

Bon ba je vais essayer de faire sa a tete reposer et surtout de comprendre .. merci !

bon ba merci de ton aide mais j'ai toujours rien compris jcomprend pas pourquoi on prend zéro et tout .. bref tempis .. merci quand même !

montre moi alors comment tu étudies le signe de 2-x sur l'intervalle [-1;3]

avant de trouver le signe il faut d'abord trouver où la dérivée s'annule je sais le faire mais pour cette expression je n'y arrive pas , je te donne un exemple : 2x+6
x= 6 / 2 = 3  donc je conclut que la dérivée 2x+6 s'annule à 3 .   seulement pour la dérivée
3x( 2-x)  je n'arrive pas à procédé ..  sa c'était le premier point .

Ensuite deuxieme point il faut trouver le signe de la dérivée , sachant que mon intervalle et de [ -1 ; 3 ] ,  moi ce que j'aurer fait  pour le -1 j'aurer remplacer -1 dans la dérivée     3x ( 2-x ) donc : 3 * ( -1 ) + 2 * - ( -1 ) = ...

et pour 3 j'aurer fait 3x ( 2-x) : 3*3 + 2* ( -3 ) = ...

mais je ne croit pas que se soit comme sa ..
seulement je fait toujours une méthode semblable sauf que quand je fait sa généralment il ya un seul x donc sa me semble plus simple .. comme : 2x + 6  .  Sauf que là ia 2 x et non 1 seul .. pour 3x ( 2- x ) .

Bon ben je fais la même chose que toi, sauf que l'expression est une multiplication de deux expressions on a 3x * (2-x), tu te rappelles peut-être on appelle ça des équations produit en troisième c'est du style 3x*(2-x) = 0.
Or un produit est nul si un de ses termes est nul ; donc 3x (2-x)=0 :
3x=0 ou 2-x = 0
donc 3x=0 si x=0 et 2-x = 0 si x = 2
tu as ce qu'on appelle les racines de 3x *(2-x) (les x qui annulent la dérivée)

maintenant tu peux étudier le signe de 3x (2-x) :
je te rappelle que tu as les racines     0       2
tu vas chercher le signe quand x est < 0 quand il est entre 0 et 2 et quand x est > 2.

Pour ça tu choisis des valeurs  : pour x < 0 tu prends -1 et tu calcules f'(-1) on aura f'(-1)= 3*(-1) *(2-(-1)) = -3*(2+1)= -9 donc c'est négatif
pour x entre -1 et 2 le plus simple est de prendre 1 et on aura f'(1)=3*1(2-1)=3 ce qui est positif
enfin pour x > 2 tu prends 3 et f'(3)=3*3(2-3)=3*-1=-3 ce qui est négatif

finalement tu as la dérivée f'(x) qui est négative quand x<0, positive quand x est entre 0 et 2 et à nouveau négative quand x est > 2

oui d'accord mais tu na pas  utilisé l'intervalle -1 ; 3 ??

ben si j'ai pris -1 pour calculer f'(-1) puis 3 pour f'(3)

puis 0 et 2 appartiennent également à l'intervalle [1;3]

d'aacord donc tu as calculer pour x<0   , pour x entre -1 et 2   et pour x > 2  mais cetait necessaire de le calculer pour x entre -1 et 2 ?

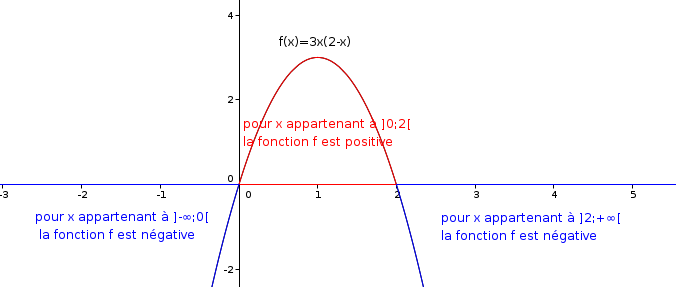
si tu regardes le graphique tu verras que entre -1 et et 0 la fonction dérivée est négative (en dessous de l'axe des abscisses en bleu) que pour x entre 0 et 2 la fonction dérivée est positive (au dessus de l'axe des abscisses en rouge) et finalement pour x > 2 la fonction dérivée redevient négative (en dessous de l'axe des abscisses en bleu)
Maintenant que tu as le tableau de signes de f'(x) tu peux en déduire les variations de f.

par contre je comprend pas ton tableaux car moi par exemple on les faits comme sa :

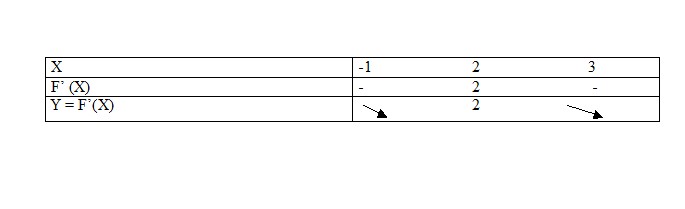
mon tableau n'est pas un tableau de variation comme le tien c'est un tableau de signes. Le tableau de variation correspondant à ta fonction f le voici :

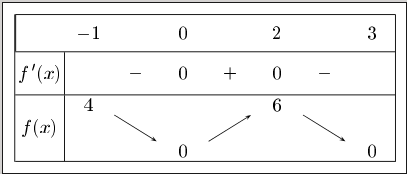
tu vois dans la ligne f'(x) on retrouve les résultats de ma dernière ligne du tableau de signes

oui et  4   et 6 sa corespond a quoi ??

f(-1)=4 et f(2)=6,

Quand tu dit f(-1)  cest 3 * (-1) * 2 - (-1)  ?
est f(2) cest  3*2*2-2 ?

Nan ?

cest pas f de 3 quon calcul ?

quand je dis f(-1) c'est avec f(x)=3x²-x³ pareil pour f(2)=3*2²-2³=12-8=4 et f(-1)=3*(-1²)-(-1)³=4, il y a une erreur pour f(2) dans le tableau de variation, il faut remplacer le 6 par un 4.

oui cest vrai exacte sa fait 4 et non 6 donc en gros quand jdesinerer ma courbe l'axe des abscisse X passera par -1 , 0, 2, 3 et l'axe des ordonné Y passera par 4, 0, 4, 0

comme ça pas d'erreur possible :

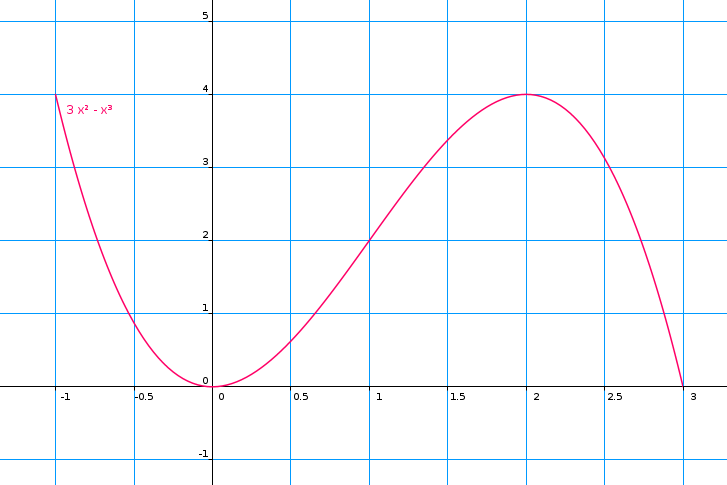
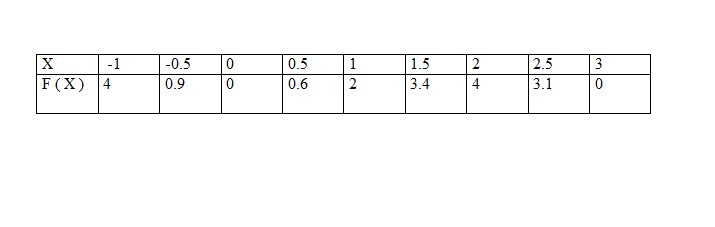
Oui sauf que je pense que la courbe ne sera pas comme sa car après j'ai calculer mon tableaux de valeur ci dessous sachant qu'il faut tracer la courbe C ainsi que les tangentes à la courbe aux points d'absisse 0 et 2 .   echelle :absisse : 5 cm  pour 1  ;  ordonné : 2cm pour 1

tableaux que j'ai remplie pour realiser la courbe :

avec les données que tu as tu obtiendras la même courbe même si ce n'est pas à la même échelle, l'allure sera identique.
Pour les tangentes c'est pas compliqué pour x=0 c'est l'axe des abscisses et pour x=2 c'est la parallèle à l'axe des abscisses passant par le point (2,4)

Jai fait ma courbe sa me donne tu as raison pareille après pour les tengentes jai ai que une a tracé vu que l'autre c'est les abcsisse et sinon j'avais l'équation -x² + 4 x - 3 = 0

j'ai fait sa : delta = b ² - 4 * ac
delta= 4² - 4 * (-x) * (-3)
delta= 16- 12 x
delta = 28 donc delta superieur à 0 donc il y a deux solutions :

x 1 = - b + racine carré delta / 2 a
x1 = -4 + racine carré de 28 / 2 * a
x1 = -4 + 5 / x² = 1 / x²

x2= -b - racine carré delta/ 2 a
x2= -4 - racine carré de 28 / 2* a
x2= -4 - 5 / x² = -9/ x²

donc s =[  1/x² ; -9/x² ]


Jvoulais savoir si sa te sembler juste ??

enfete  non jme suis tromper jai trouver mon ereur  c pas sur x² paske on lremplace par 1  ^^

pourquoi x dans le calcul de quand tu as -x²+4x-3=0
a=-4
b=4
c=-3
b²-4ac=16-4*(-1)*(-3)=16-12=4=2²

x₁=(-4+2)/-2 = 1

x₂=(-4-2)/-2=3

Oui oui cest se que j'ai fait c'est ce que j'avait rectifier parce que javer oublier de remplacer - x²  par -1 mais cest bon là .

Sinon avec quel logiciel tu fait tes courbes et tout ??

avec Geogebra pour les courbes et la géométrie c'est un logiciel gratuit.
Pour les formules soit j'utilise l'éditeur LaTex d'ici ou je tape les formules avec Dmaths dans open office et je fais une capture d'écran. Les logiciels que j'utilise sont tous gratuits, j'ai banni Microsoft de mon ordinateur depuis quelques années ...