Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première DérivationTopics traitant de dérivation [tout]Lister tous les topics de mathématiques

1 2 3 +

Niveau première
Partager :

Fonctions dérivées

Posté par Profil Devoirs33 23-10-21 à 13:35

Bonjour à tous,

Pouvez-vous m'aider pour cette exercice s'il vous plaît, merci.

Exercice 1 :

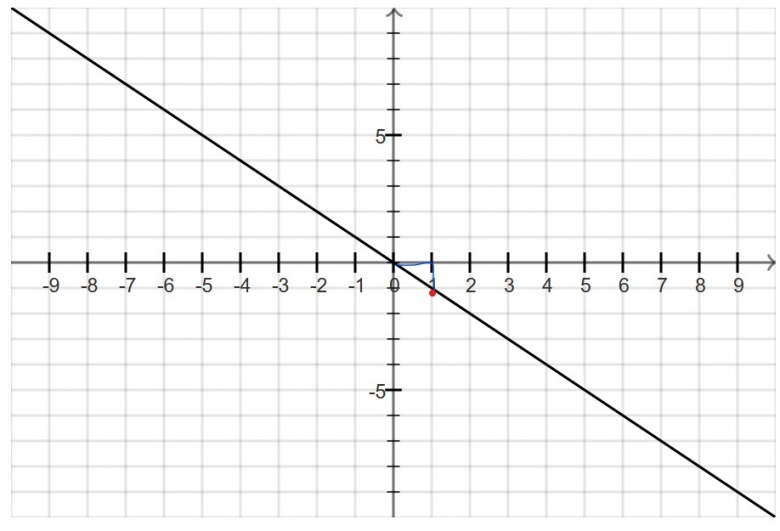
a) Déterminer le coefficient directeur de la droite ( en pièce jointe )

   ° Je trouve a = -1.

b) Donner l'équation de la tangente à la courbe

(C) : y = 6x-6/-9x+3
au point d'abscisse -2

    ° y = f(a) + f'(a) (x-a)

Je calcule d'abord le taux de variation

f(-2) = 6*(-2)-6/-9*(-2)+3 = -6/7
f(-2+h) = 6*(-2+h)-6/-9*(-2+h)+3 = -6+2h/7-3h

(-6+2h/7-3h) - ((-6/7)/h

Suis-je sur la bonne voie ? Je n'ai pas l'impression.

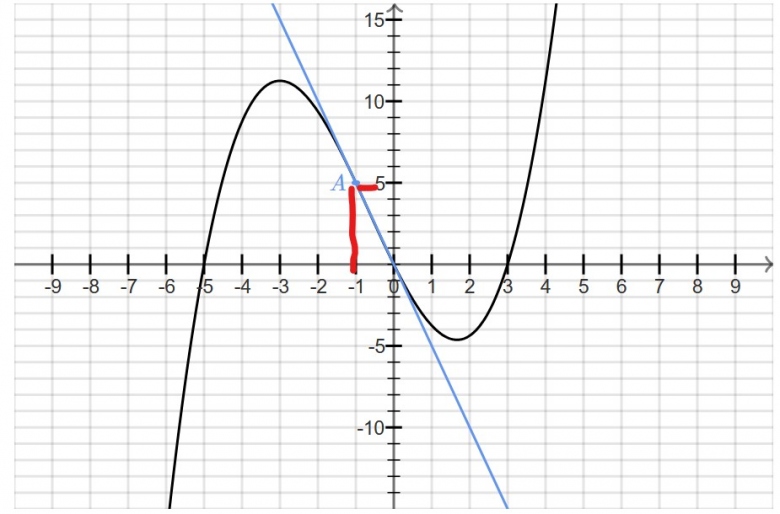
c)Soit f une fonction représentée par la courbe ci-dessous. ( en pièce jointe)
Déterminer graphiquement f​′​​(−1)

    ° Graphiquement je trouve 5

d)
Quelle est la dérivée de la fonction f ?
On admettra qu'elle est dérivable sur chaque intervalle contenu dans son domaine de définition
D = R \ {-3/5}

f:x↦ −7x+6/5x+3

Merci à tous et bonne journée.

Fonctions dérivées

Fonctions dérivées

Posté par
Leilere : Fonctions dérivées 23-10-21 à 13:48

Bonjour,

a)  a=-1  c'est juste.

b)  précise l'expression, stp, mets des parenthèses !

Posté par
heklare : Fonctions dérivées 23-10-21 à 13:52

Bonjour
Vous avez encore oublié les parenthèses
  pour le coefficient de la droite  oui -1

taux de variation  f(x)=\dfrac{6x-6}{-9x+3}=\dfrac{2x-2}{-3x+1}

il manque les parenthèses

f(-2)=\dfrac{-6}{7} \quad f(-2+h)=\dfrac{6(-2+h)-6}{-9(-2+h)+3}=\dfrac{-18+6h}{21-9h}
réduction au même dénominateur

Posté par
heklare : Fonctions dérivées 23-10-21 à 13:56

c) la dérivée en -1 est nécessairement négative. Ce ne peut donc pas être 5

d) vu l'ensemble de définition il manque les parenthèses f(x)=\dfrac{-7x+6}{5x+3}

Posté par
Leilere : Fonctions dérivées 23-10-21 à 13:56

bonjour hekla,
je te laisse poursuivre (je crois que tu as déjà pas mal travaillé avec Devoirs33).
Bonne journée

Posté par
heklare : Fonctions dérivées 23-10-21 à 13:58

Bonjour Leile

Bonne journée

Posté par Profil Devoirs33re : Fonctions dérivées 23-10-21 à 17:46

b) Vous aviez divisé par 3 afin de rendre l'expression plus simplifié mais, a t'on le droit ?
f(-2) = -6/7
f(-2+h) = -18+6h/21-9h
(-18+6h+6/7)/h

c) graphiquement, f'(-1) = -5,2 ?

Posté par
heklare : Fonctions dérivées 23-10-21 à 18:05

a)N'est-il demandé que le coefficient directeur  ?

b) Si au lieu de 6/9  on écrit 2/3 a-t-on changé quelque chose ?

On ne peut pas prendre par exemple g=\dfrac{1}{3} f , car alors ce n'est plus identique

Vous voyez bien que l'on a la même valeur pour f(-2)
On vous demande l'équation de la tangente en -2
vous ne l'avez pas donné, vous n'avez pas donné non plus f'(-2)

\displaystyle \lim_{h\to 0}\left(\dfrac{f(-2+h)-f(-2)}{h}\right) = ?


c) Le point A a pour coordonnées (-1~;~5). La droite passe par l'origine donc le coefficient
directeur est -5. Comme le coefficient directeur de la tangente en un point est le nombre dérivé
de la fonction en ce point, on a donc

f'(-1)=-5

Posté par Profil Devoirs33re : Fonctions dérivées 23-10-21 à 18:12

a) Oui uniquement le coefficient directeur.

b) f(-2+h)-f(-2)/h
( -18+6h) / 21 - 9h - (-6/7) / h

Posté par Profil Devoirs33re : Fonctions dérivées 23-10-21 à 18:14

c) Comment vous aviez fait pour trouver le coefficient directeur -5 ?

Posté par
philgr22re : Fonctions dérivées 23-10-21 à 18:24

Bonsoir,
* Modération > Intervention inutile effacée : le sujet est déjà pris en charge par un autre aidant *

Posté par
heklare : Fonctions dérivées 23-10-21 à 18:27

Il faut continuer jusqu'à ce que vous ayez le nombre dérivé


Pour la lecture, vous l'avez effectué à la question a)   comment avez-vous trouvé -1 alors ?
C'est le même principe

Posté par Profil Devoirs33re : Fonctions dérivées 23-10-21 à 18:40

Oui c'est juste qu'il y a une courbe et une droite, ce qui m'a beaucoup perturbé pour déterminer le coefficient directeur.


-18 + 6h / 21 - 9h     -    (6/7)   / h

= - 18 / 21 - 9h  -   7 /   h
= -25 / 21 - 9h  / h        ( suis-je sur la bonne voie ?)

Posté par Profil Devoirs33re : Fonctions dérivées 23-10-21 à 18:42

par contre je n'arrive pas à comprendre la manière dont vous avez trouvé -5 parce qu'il y a une courbe et une droite, cela me perturbe.

Posté par
philgr22re : Fonctions dérivées 23-10-21 à 18:45

Tu ne peux pas parler de coefficient directeur d('une courbe....

Posté par
philgr22re : Fonctions dérivées 23-10-21 à 18:46

* Modération > Idem. *

Posté par
heklare : Fonctions dérivées 23-10-21 à 18:47

Bonne soirée

Posté par Profil Devoirs33re : Fonctions dérivées 23-10-21 à 18:47

oui mais la consigne c'est déterminer graphiquement,
du coup, je pensais qu'il ne faut pas faire de calcul

Posté par Profil Devoirs33re : Fonctions dérivées 23-10-21 à 18:50

pour la b :
-18 + 6h / 21 - 9h     -    (6/7)   / h

= - 18 / 21 - 9h  -   7 /   h
= -25 / 21 - 9h  / h

Posté par
philgr22re : Fonctions dérivées 23-10-21 à 18:54

Difference d'ordonnées/difference d'abscisses Ce n'est pas un calcul trop long!

Posté par Profil Devoirs33re : Fonctions dérivées 23-10-21 à 18:55

il fallait faire : xB - xA / yB - yA ?

Posté par Profil Devoirs33re : Fonctions dérivées 23-10-21 à 19:00

Est-ce que vous pouvez annoter la pièce jointe n°2 afin d'expliquer la façon dont vous avez procédé pour trouver -5 si cela ne vous dérange pas ?

Posté par
philgr22re : Fonctions dérivées 23-10-21 à 19:01

Mais fais tu attention à ce que tu lis???

Posté par
philgr22re : Fonctions dérivées 23-10-21 à 19:02

Tu as inversé la fraction que je t'ai rappelée

Posté par Profil Devoirs33re : Fonctions dérivées 23-10-21 à 19:03

Difference d'ordonnées/difference d'abscisses

Je n'ai jamais vu cette notion.
Que signifie la différence d'un ordonné et d'une abscisse ?

Posté par
philgr22re : Fonctions dérivées 23-10-21 à 19:03

Il me semble t'avoir deja donné des conseils de methode dans un exercice precedent...

Posté par Profil Devoirs33re : Fonctions dérivées 23-10-21 à 19:04

Je comprends mieux visuellement sur un graphique

Posté par
philgr22re : Fonctions dérivées 23-10-21 à 19:05

Respire un bon coup!!
ordonnéetu connais
abscisse tu connais
difference tu connais
definition du coefficient directeur donnée en seconde ,tu connais

Posté par
philgr22re : Fonctions dérivées 23-10-21 à 19:06

Bah il s'agit d'une definition graphique :tu te deplaces d'un point à un autre avec le triangle rectangle correspondant à la variation d'ordonnées en premier suivie de la variation en abscisses ensuite

Posté par Profil Devoirs33re : Fonctions dérivées 23-10-21 à 19:09

D'accord.

Pouvez-vous m'aider pour la b) ?
Pour l'instant j'ai essayé de d'appliquer la formule pour trouver le taux d'accroissement mais je ne l'ai pas achevé.

-18 + 6h / 21 - 9h     -    (6/7)   / h

= - 18 / 21 - 9h  -   7 /   h
= -25 / 21 - 9h  / h

Posté par
philgr22re : Fonctions dérivées 23-10-21 à 19:13

Tu as deja une faute de signe au depart puisque tu soustrais f(-2) et attention au manque de ().

Posté par
philgr22re : Fonctions dérivées 23-10-21 à 19:14

hekla t'avais guidé

Posté par
philgr22re : Fonctions dérivées 23-10-21 à 19:16

laisse le h du denominateur de côté pour le moment et reduis au maximum le numerateur

Posté par Profil Devoirs33re : Fonctions dérivées 23-10-21 à 19:19

oui il m'a emmené jusqu'à l'obtention  de :

f(-2+h)-f(-2)/h
( -18+6h) / 21 - 9h - (-6/7) / h


(-18 + 6h) / 21 - 9h +  (6/7)  

= (- 18 / 21) - 9h  - 7
= (-25 / 21) - 9h  

Posté par
philgr22re : Fonctions dérivées 23-10-21 à 19:22

Met une () au denominateur de ta fraction et reprend le calcul à ton premier signe =

Posté par
philgr22re : Fonctions dérivées 23-10-21 à 19:23

Une remarque ;es tu sur de la fraction donnée dans ton enoncé car elle est simplifiable!

Posté par Profil Devoirs33re : Fonctions dérivées 23-10-21 à 19:24

non je suis sur la fraction donnée par hekla.

Posté par Profil Devoirs33re : Fonctions dérivées 23-10-21 à 19:26

(- 18 / (21)) - 9h  - 7

après ça je ne sais pas quoi faire.
je soustrais -7 et -18 ?

Posté par
philgr22re : Fonctions dérivées 23-10-21 à 19:27

C'est faux

Posté par
philgr22re : Fonctions dérivées 23-10-21 à 19:28

pars de (2x-2)/(-3x+1)

Posté par Profil Devoirs33re : Fonctions dérivées 23-10-21 à 19:33

y = (2x-2)/(-3x+1)

f(2+h) - f(-2) / h


f(2+h) = (-18+6h)/(21 - 9h)
f(-2) = (-6/7)

Donc : (-18+6h)/(21 - 9h) - (-6/7)  Jusqu'ici c'est correct ?

Posté par
philgr22re : Fonctions dérivées 23-10-21 à 19:35

Non tu es partie de la fraction non simplifiée....rectifie ,ce qui evient à simplifier ta premiere fraction et met ensuite au meme denominateur

Posté par
philgr22re : Fonctions dérivées 23-10-21 à 19:38

f(-2+h)= (2(-2+h-2)/(-3(-2+h)+1)=....

Posté par
philgr22re : Fonctions dérivées 23-10-21 à 19:39

pardon j'ai oublié une ()
(2(-2+h)-2)/(-3(-2+h)+1)

Posté par Profil Devoirs33re : Fonctions dérivées 23-10-21 à 19:40

= -8 + 2h / 7 - 3h

Posté par Profil Devoirs33re : Fonctions dérivées 23-10-21 à 19:41

= (-8+2h) / (7-3h)

Posté par
philgr22re : Fonctions dérivées 23-10-21 à 19:41

c'est -6 au lieu de -8

Posté par
philgr22re : Fonctions dérivées 23-10-21 à 19:43

maintenant tu ajoutes 6/7 en mettant au meme denominateur.Ensuite tu n'oublies pas de mettre l'expression reduite sur h et tu simplifies par h . Je dois partir .a plus tard si personne ne prend le relai

Posté par Profil Devoirs33re : Fonctions dérivées 23-10-21 à 19:43

D'accord.

f(-2+h) = (-6+2h) / (7-3h)

et f(-2) = (-6/7)

Posté par Profil Devoirs33re : Fonctions dérivées 23-10-21 à 19:45

"maintenant tu ajoutes 6/7"

Je dois soustraire avec non ?

1 2 3 +


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !