Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... TrigonométrieTopics traitant de trigonométrie [tout]Lister tous les topics de mathématiques
Niveau Prepa (autre)
Partager :

Fonctions trigonométriques

Posté par
matheux14 06-11-21 à 13:40

Bonjour,

1) Calculer la dérivée des fonctions j(x)= Arc \tan (\sin 3x)

2) Soit f : x \mapsto arc \sin \left(\dfrac{1}{\cos h (x)}\right)-arc \sin \left(\dfrac{\sin h (x)}{\cos h (x)}\right). Calculer f'. En déduire l'expression de f.

2) j(x) = [f \circ g] (x) avec f(x) = arc tan x et g(x) = sin 3x

\left([f \circ g] (x)  \right)' = \left([f' \circ g] (x)  \right) * g'(x)

*f'(x) = \dfrac{1}{x²+1} et g'(x) = 3 \cos 3x

Donc \left([f \circ g] (x)  \right)' = \dfrac{1}{9 \cos² 3x +1}*3 \cos 3x

j'(x) = \dfrac{3 \cos 'x}{ç \cos² 3x +1}

2) f'(x) =\left(arc \sin \left(\dfrac{1}{\cos h (x)}\right)-arc \sin \left(\dfrac{\sin h (x)}{\cos h (x)}\right)\right)'

f'(x) = \left[arc \sin \left(\dfrac{1}{\cos h (x)}\right) \right]' - \left[arc \sin \left(\dfrac{\sin h (x)}{\cos h (x)}\right) \right]'

Posons P(x) =arc \sin \left(\dfrac{1}{\cos h (x)}\right) et G(x) =arc \sin \left(\dfrac{\sin h (x)}{\cos h (x)}\right)

P'(x) =\left[arc \sin \left(\dfrac{1}{\cos h (x)}\right)\right]'

p(x) = [p_{1} \circ p_{2}](x) avec p1(x) = arc sin x et p_2 (x) = \dfrac{1}{\cos h x}

p'(x)=\left([p_{1} ' \circ p_{2}] (x)  \right) * p_{2} '(x)

p' _{1} (x) = \dfrac{1}{\sqrt{1-x²}} et p'_{2} (x) =\dfrac{\sin h (x)}{\cos h ²(x)}

D'où p'(x) =\dfrac{1}{\sqrt{1-\dfrac{1}{\cos h² (x)}}} * \dfrac{\sin h (x)}{\cos h² (x)}

*g(x) = [g_{1} \circ g_{2}](x) avec g_{1} (x) = arc \sin(x) et g_{2} (x) = \dfrac{\sin h (x)}{\cos h(x)}

g'(x)=\left([g_{1} ' \circ g_{2}] (x)  \right) * g_{2} '(x)

g'{1} (x) = \dfrac{1}{\sqrt{1-x²}} et p'_{2} (x) = \dfrac{\sin h' (x) \cos h x - \sin h (x) \cos h '(x)}{\cos h ² (x)} = \dfrac{\cos h ² (x) - \sin h ² (x)}{\cos h² (x)} = \dfrac{1}{\cos h² (x)}

g'(x)= \dfrac{1}{\sqrt{1-\dfrac{\sin h(x)}{\cos h (x)}}} * \dfrac{1}{\cos h² (x)}

f'(x) = \dfrac{1}{\sqrt{1-\dfrac{1}{\cos h² (x)}}} * \dfrac{\sin h (x)}{\cos h² (x)} - \dfrac{1}{\sqrt{1-\dfrac{\sin h(x)}{\cos h (x)}}} * \dfrac{1}{\cos h² (x)}

Mais il me semble que Geogebra ne me confirme pas..

Sinon, comment faire pour trouver l'expression de f ?

Posté par
carpediemre : Fonctions trigonométriques 06-11-21 à 13:46

salut

il y a évidemment plein de simplifications à faire !!!

connaissant les propriétés algébriques des fonctions cosh et sinh ...

toutes ces formules avec des primes sont inutiles et une perte de temps ...

1/est faux ... entre autre ...

Posté par
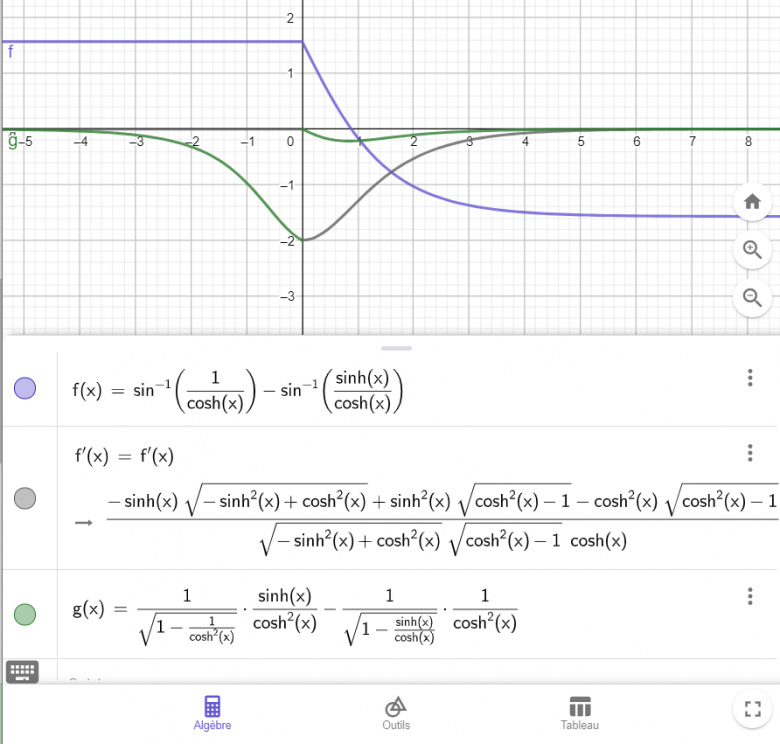
matheux14re : Fonctions trigonométriques 06-11-21 à 13:55

Oups c'est une erreur de frappe j'(x) = \dfrac{3 \cos 3x}{9 \cos² 3x +1}

Posté par
carpediemre : Fonctions trigonométriques 06-11-21 à 14:03

faux ...

Posté par
matheux14re : Fonctions trigonométriques 06-11-21 à 16:25

Oui désolé c'est j'(x) = \dfrac{3 \cos 3x}{\sin² 3x +1}

Pour la deuxième dérivée je dois mettre au même dénominateur ?

Posté par
matheux14re : Fonctions trigonométriques 06-11-21 à 21:45

Fonctions trigonométriques

f' est celle donnée par géogebra et g(x) est celle que je trouve..

Pourtant je n'ai pas fait d'erreur

Comment trouver l'expression de la fonction f ?

Posté par
carpediemre : Fonctions trigonométriques 06-11-21 à 22:49

carpediem @ 06-11-2021 à 13:46

il y a évidemment plein de simplifications à faire !!!

connaissant les propriétés algébriques des fonctions cosh et sinh ...

Posté par
matheux14re : Fonctions trigonométriques 07-11-21 à 09:56

f'(x) = \dfrac{\sqrt{e^{-x} \cos h(x) ^{3}}-\cos h (x)}{\sqrt{e^{-x} \cos h^5 (x)}

Posté par
matheux14re : Fonctions trigonométriques 07-11-21 à 10:03

f'(x) = \dfrac{\sqrt{e^{-x} \cos h ^{3}(x)} - \cos h(x)}{\sqrt{e^{-x} \cos h^{5}(x)}}

Posté par
carpediemre : Fonctions trigonométriques 07-11-21 à 12:12

je ne sais pas si c'est exact mais on peut encore simplifier : dans les racines tout d'abord puis la fraction ensuite ...

Posté par
carpediemre : Fonctions trigonométriques 07-11-21 à 12:12

mais si c'est la 2/ je suis étonnée de ne pas voir de somme ...

Posté par
matheux14re : Fonctions trigonométriques 07-11-21 à 12:22

D'accord mais est-ce qu'uo est nécessaire d'avoir une somme et pourquoi ?

Posté par
carpediemre : Fonctions trigonométriques 07-11-21 à 12:25

si f = u + v alors f' = u' + v' ...

Posté par
matheux14re : Fonctions trigonométriques 07-11-21 à 18:59

Je crois que la forme la plus simplifiée est : \dfrac{\sqrt{e^{-x} cos h(x)}-1}{\sqrt{e^{-x} \cos h ^3(x)}} à moins qu'on utilise la forme exponentielle pure..

Posté par
matheux14re : Fonctions trigonométriques 09-11-21 à 09:36

Bonjour, j'ai revérifié les calculs et je trouve :

f'(x) = \dfrac{-\sin h (x) +\sin h² (x) |\sin h(x)| -\cos h²(x) |\sin h(x)|}{|\sin h(x)| \cos h(x)}

\forall x \ge 0 ; \sin h(x) \ge 0 \Rightarrow |\sin h(x)|= \sin h(x) donc f'(x)=-\dfrac{2}{\cos h(x)}

\forall x \le 0 ; \sin h(x)\le 0 \Rightarrow |\sin h(x)| \le 0 il vient f'(x) = 0

Posté par
matheux14re : Fonctions trigonométriques 09-11-21 à 09:48

\forall x \le 0 ; f'(x) = 0 \iff f(x) = k ; k \in \R

On calcul f(0) =  arc \sin \left(\dfrac{1}{\cos h (0)}\right)-arc \sin \left(\dfrac{\sin h (0)}{\cos h (0)}\right)=arc \sin (1)-arc \sin (0) = \dfrac{\pi}{2}

Donc \forall x \le 0 ; f(x) = \dfrac{\pi}{2}.

Et \forall x \ge 0 ; f(x) = arc \sin \left(\dfrac{1}{\cos h (x)}\right)-arc \sin \left(\dfrac{\sin h (x)}{\cos h (x)}\right)


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !